Integrated Rate Laws - Zero, First, & Second Order Reactions - Chemical Kinetics
TLDRThe video script discusses integrated rate law problems, focusing on zero, first, and second-order reactions. It explains how the rate of reaction depends on the concentration of reactants and introduces the rate constant k. The script also covers the units of k, half-life concepts, and how they relate to reaction orders. Various examples and problems are provided to illustrate the calculations involved in determining reaction rates, half-lives, and the initial concentrations of reactants. The importance of understanding the relationship between reaction order, rate constant, and concentration is emphasized to predict and analyze chemical reactions effectively.
Takeaways
- 📝 The rate law expression varies for different ordered reactions: zero order (rate = k), first order (rate = k[A]^1), and second order (rate = k[A]^2).
- 🔄 The concentration of reactants affects the reaction rate differently based on the reaction order: higher order reactants have a greater impact on the reaction rate.
- 📈 For zero-order reactions, doubling or tripling the concentration of the reactant does not change the reaction rate, whereas for second-order reactions, the rate increases by the square of the concentration change.
- 🌀 The units of the rate constant (k) change with the order of the reaction: m^(1-n) * t^(-1), where n is the reaction order.
- 🕰️ Half-life is a measure of time for the concentration of a reactant to decrease by half and varies depending on the reaction order: zero-order (t1/2 = [A]0 / (2k)), first-order (t1/2 = ln(2) / k), and second-order (t1/2 = 1 / (k[A]0)).
- ⏫ The half-life for a first-order reaction is independent of the initial concentration of the reactant, while for zero-order and second-order reactions, it depends on the initial concentration.
- 📉 In a zero-order reaction, increasing the initial concentration increases the half-life, whereas in a second-order reaction, increasing the initial concentration decreases the half-life.
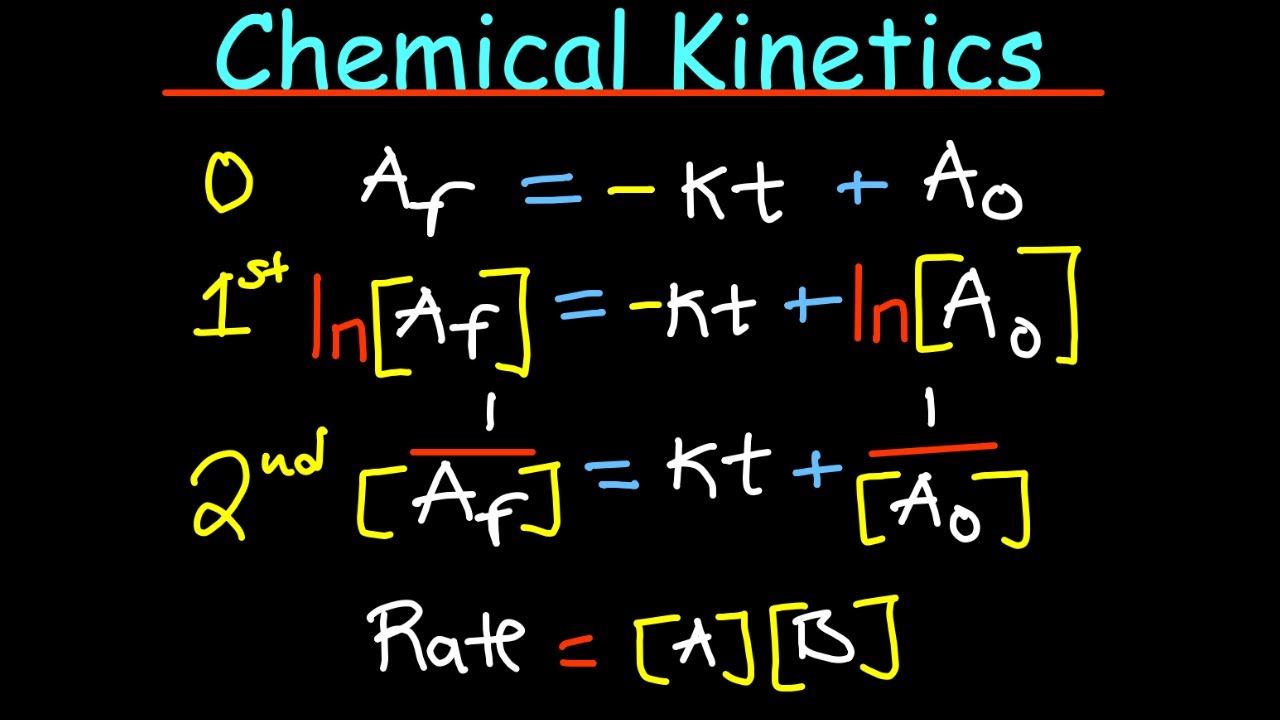
- 📊 Integrated rate law expressions are used to determine the concentration of reactants over time for zero-order (final concentration = -kt + initial concentration), first-order (ln(final concentration) = -kt + ln(initial concentration)), and second-order (1/final concentration = kt + 1/initial concentration) reactions.
- 🎨 Plotting data for reaction orders: zero-order (concentration vs. time), first-order (ln(concentration) vs. time), and second-order (1/concentration vs. time) yield straight lines with slopes indicative of the reaction rate.
- 🧠 Understanding the relationship between reaction order, rate constant units, and the impact on reaction rate is crucial for solving chemical kinetics problems and predicting reaction outcomes.
Q & A
What is the rate law expression for a zero-order reaction?
-For a zero-order reaction, the rate law expression is rate = k, where k is the rate constant and the rate is independent of the concentration of the reactant.
How does the rate of a first-order reaction change with the concentration of the reactant?
-In a first-order reaction, the rate is directly proportional to the concentration of the reactant. If the concentration of the reactant doubles, the rate also doubles, and if it triples, the rate triples.
What is the relationship between the rate of a second-order reaction and the concentration of the reactant?
-For a second-order reaction, the rate is proportional to the square of the concentration of the reactant. If the concentration doubles, the rate increases by a factor of 4 (2^2), and if the concentration triples, the rate increases by a factor of 9 (3^2).
What are the units of the rate constant k for different orders of reactions?
-The units of k are m^(1-n) * t^(-1), where m represents the concentration units, n is the order of the reaction, and t is the time units. For zero-order, k has units of m^0 * t^(-1), for first-order, k has units of m^(-1) * t^(-1), and for second-order, k has units of m^(-2) * t^(-1).
How does the half-life of a reactant change with the initial concentration for zero-order, first-order, and second-order reactions?
-For a zero-order reaction, the half-life is directly proportional to the initial concentration. For a first-order reaction, the half-life is independent of the initial concentration. For a second-order reaction, the half-life is inversely proportional to the initial concentration.
What is the integrated rate law expression for a zero-order reaction?
-The integrated rate law expression for a zero-order reaction is [Final Concentration] = (-k * t) + [Initial Concentration], where k is the rate constant, t is the time, and the initial and final concentrations are in molarity (m).
What is the integrated rate law expression for a first-order reaction?
-The integrated rate law expression for a first-order reaction is ln([Final Concentration]) = -k * t + ln([Initial Concentration]), where k is the rate constant, t is the time, and the initial and final concentrations are in molarity (m).
What is the integrated rate law expression for a second-order reaction?
-The integrated rate law expression for a second-order reaction is (1 / [Final Concentration]) = k * t + (1 / [Initial Concentration]), where k is the rate constant, t is the time, and the initial and final concentrations are in molarity (m).
How can you determine the order of a reaction if it is not specified?
-You can determine the order of a reaction by examining the units of the rate constant k. If k has units of time^(-1) (like s^(-1), min^(-1), etc.) without any concentration units, it indicates a first-order reaction. If the units include concentration units (like m^(-1), m^(-2), etc.), you can use the formula m^(1-n) * t^(-1) to solve for the order n.
How does the slope of a plot reflect the order of a reaction?
-The slope of a plot reflects the order of a reaction in the following way: for a zero-order reaction, the plot of concentration versus time has a negative slope; for a first-order reaction, the plot of the natural log of concentration versus time has a negative slope; and for a second-order reaction, the plot of the reciprocal of concentration versus time has a positive slope.
What is the relationship between the rate constant k and the half-life of a reaction?
-The relationship between the rate constant k and the half-life of a reaction depends on the order of the reaction. For a first-order reaction, the half-life is independent of the initial concentration and is directly related to the rate constant k, with the half-life being ln(2) / k. For a second-order reaction, the half-life is inversely related to the rate constant, with the half-life being 1/(k * [Initial Concentration]). For a zero-order reaction, the half-life is directly proportional to the initial concentration and independent of the rate constant.
Outlines
📝 Introduction to Integrated Rate Law Problems
This paragraph introduces the topic of integrated rate law problems, emphasizing the importance of understanding how to solve them. It explains the basics of rate law expressions for different ordered reactions, such as zero order (rate = k), first order (rate = k[A]), and second order (rate = k[A]^2). The paragraph highlights how the order of a reaction affects the rate of chemical reactions, with higher order reactants having a greater impact on the reaction rate. It also delves into the units of the rate constant (k) for each order of reaction, providing a general equation to determine these units based on the reaction order.
🕰️ Half-Life Concepts and its Dependency on Reaction Order and Concentration
This section discusses the concept of half-life, a measure of time taken for the concentration of a reactant to decrease by half. It explains how the half-life varies for zero-order, first-order, and second-order reactions, depending on the initial concentration of the reactant and the rate constant (k). The paragraph emphasizes that the half-life for first-order reactions is independent of the initial concentration, while for zero-order and second-order reactions, it is directly and inversely proportional, respectively. The impact of the rate constant on half-life across all reaction orders is also highlighted, noting that an increase in k results in a decrease in half-life.
📈 Integrated Rate Law Equations and their Graphical Representation
This paragraph presents the integrated rate law expressions for zero-order, first-order, and second-order reactions, explaining their graphical representations. It details the equations in slope-intercept form and describes the corresponding straight-line graphs that result from plotting concentration versus time for each reaction order. The paragraph also provides a method for determining the units of the rate constant (k) based on the reaction order and discusses the implications of these units on the overall reaction dynamics.
🧠 Problem Solving: Identifying Reaction Orders and Calculating Reaction Parameters
The paragraph focuses on problem-solving techniques for identifying the order of a chemical reaction and calculating various reaction parameters such as the rate constant (k) and half-life. It presents a series of questions that require the application of integrated rate law concepts, the use of the rate constant's units to determine reaction order, and the calculation of reaction outcomes based on initial and final concentrations, as well as the time taken for reactions to proceed. The paragraph serves as a practical guide for understanding and applying chemical kinetics principles.
🕒 Calculation of Reactant Concentrations and Half-Life for Specific Reaction Scenarios
This section provides detailed calculations for specific scenarios in zero-order reactions, including determining the new concentration of a reactant after a given time and calculating the time required for the concentration to reach a certain value. It also explains how to calculate the initial concentration of a reactant given the final concentration and the time taken to reach it, using the integrated rate law expressions for zero-order reactions. The paragraph demonstrates the application of these calculations through a step-by-step approach, reinforcing the understanding of reaction dynamics and the impact of reaction order on concentration changes over time.
🔢 Determining Reaction Order from Rate Constant Units and Calculating Initial Concentrations
The paragraph outlines the process of deducing the order of a reaction by analyzing the units of the rate constant (k) and using this information to calculate the initial concentration of a reactant. It explains how the absence of molarity units in the rate constant indicates a first-order reaction, and it provides a method for calculating the initial concentration using the integrated rate law for second-order reactions. The paragraph also corrects a mistake in the calculation process, emphasizing the importance of accurate unit conversion and algebraic manipulation in solving chemical kinetics problems.
📊 Analyzing Data for Zero-Order Reactions and Calculating Rate Constants
This section deals with the analysis of concentration-time data for zero-order reactions and the calculation of the rate constant (k). It explains that the rate constant for a zero-order reaction is equal to the negative slope of the straight line obtained by plotting concentration versus time. The paragraph provides a step-by-step guide on how to calculate the slope from given data points and how this slope relates to the rate constant. It also addresses the concept of half-life in the context of first-order reactions and demonstrates how to calculate it using the rate constant.
🧬 Identifying Reaction Orders from Rate Changes and Determining Rate Constant Units
The paragraph focuses on determining the order of a reaction based on how the rate changes with varying concentrations of reactants. It presents a problem where the rate increases by specific factors when the concentration of reactants A and B changes. The paragraph explains how these rate changes correspond to the reaction order with respect to each reactant and how to calculate the overall reaction order. It then uses this information to deduce the units of the rate constant (k) and match it with the given options. The paragraph concludes with a comprehensive method for determining the reaction order from the units of k and the implications of these units on the reaction dynamics.
📈 Determining Overall Reaction Order from Given Rate Constant Units
This section presents a method for determining the overall order of a reaction based on the given units of the rate constant. It explains the relationship between molarity, liters, and moles, and how these units can be used to deduce the reaction order. The paragraph provides a step-by-step breakdown of the process, starting from the given units and working towards finding the overall reaction order. It concludes with the identification of the correct answer choice that corresponds to the calculated reaction order.
Mindmap
Keywords
💡Integrated Rate Law
💡Reaction Order
💡Rate Constant (k)
💡Half-Life
💡Concentration
💡Slope-Intercept Form
💡Natural Log
💡Graphs and Plots
💡Units of Measurement
💡Reaction Rate
Highlights
The video discusses integrated rate law problems and provides a method to solve them.
Zero order reaction rate is independent of the reactant concentration and is equal to k.
First order reaction rate depends on the concentration of the reactant, doubling the concentration doubles the rate.
Second order reaction rate depends on the square of the reactant concentration, doubling it quadruples the rate.
The units of the rate constant k vary based on the order of the reaction.
Half-life for a zero-order reaction is dependent on the initial concentration and the rate constant.
First order reaction half-life is independent of the initial concentration and solely depends on the rate constant.
Second order reaction half-life is dependent on both the initial concentration and the rate constant.
The rate law expression is fundamental in determining the order of a reaction.
The video provides equations for the integrated rate law expressions for zero, first, and second order reactions.
Straight line graphs for different order reactions can be used to visually represent the reaction dynamics.
The video explains how to calculate the half-life of a reaction based on its order and rate constant.
The units of k can be used to deduce the order of a reaction if it is not explicitly given.
The video provides a method to determine the order of a reaction from the units of the rate constant k.
The video demonstrates how to calculate the new concentration of a reactant after a given time in a zero-order reaction.
The video explains how to calculate the time required for a reactant concentration to reach a specific value in a zero-order reaction.
The video illustrates how to calculate the initial concentration of a reactant given the final concentration and reaction time for a specified order reaction.
The video provides a method to calculate the rate constant k from a data table showing reactant concentration over time for a zero-order reaction.
The video explains how to determine the half-life of a reaction based on its rate constant and order.
The video demonstrates how to identify the order of a reaction based on the rate of change in reaction rate with respect to reactant concentration changes.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: