MEAN, VARIANCE, AND STANDARD DEVIATION FOR UNGROUPED DATA

MATHStorya
26 Mar 202205:30
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter guides viewers through calculating the mean, population variance, and standard deviation of a set of student scores. The process involves summing the scores to find the mean, then using the variance formula to determine the spread of the data. The standard deviation is calculated by taking the square root of the variance, resulting in a mean of 12, a variance of 21, and a standard deviation of 4.58, illustrating the basic statistical measures for the given data set.

Takeaways
  • 📚 The problem involves calculating the mean, population variance, and standard deviation for a set of student scores.
  • 🔢 The mean is calculated by summing all the scores and dividing by the number of scores, resulting in a mean of 12.
  • 📉 To find the population variance, the formula used is the sum of the squared differences from the mean, divided by the number of scores (n), not n-1 as in the sample variance.
  • 📈 The scores are first adjusted by subtracting the mean to find the deviations from the mean, which are then squared for the variance calculation.
  • 📊 The squared deviations are summed up to get a total of 252, which is then divided by the number of scores (12) to find the variance, resulting in 21.
  • 📏 The standard deviation is the square root of the variance, which in this case is the square root of 21, equaling 4.58.
  • 📋 The process involves creating a table to organize the scores, their deviations from the mean, and the squared deviations.
  • 🔍 Each score is individually processed by subtracting the mean to find its deviation, which is a crucial step in variance and standard deviation calculations.
  • 📘 The script demonstrates a step-by-step approach to solving statistical problems, emphasizing the importance of each calculation step.
  • 📉 The variance gives a measure of the spread of the scores around the mean, indicating how much the scores vary.
  • 📈 The standard deviation, being the square root of the variance, provides a measure of average distance from the mean, showing the typical deviation of scores.
Q & A

  • What is the first step in solving the problem presented in the script?

    -The first step is to calculate the mean of the given student scores by adding all the numbers and dividing by the number of scores.

  • How many scores are there in the provided dataset?

    -There are 12 scores in the dataset.

  • What is the calculated mean of the scores?

    -The calculated mean of the scores is 12.

  • What is the formula for calculating the population variance?

    -The formula for calculating the population variance is the sum of the squared differences between each score and the mean, divided by the number of scores (n).

  • How do you find the difference between each score and the mean?

    -You find the difference by subtracting the mean from each individual score (x - mean).

  • What is the sum of the squared differences in the dataset?

    -The sum of the squared differences is 252.

  • How is the variance calculated from the sum of the squared differences?

    -The variance is calculated by dividing the sum of the squared differences (252) by the number of scores (12).

  • What is the calculated variance of the scores?

    -The calculated variance of the scores is 21.

  • What is the standard deviation and how is it related to variance?

    -The standard deviation is the square root of the variance, which measures the amount of variation or dispersion in the dataset.

  • What is the calculated standard deviation of the scores?

    -The calculated standard deviation of the scores is approximately 4.58.

  • Why is the square of a negative number always positive?

    -The square of a negative number is always positive because multiplying two negative numbers results in a positive product.

  • How does the script use the table to solve the problem?

    -The script uses the table to organize and calculate the differences from the mean, their squares, and then to sum these values for variance and standard deviation calculations.

Outlines
00:00
📊 Calculating Mean, Variance, and Standard Deviation

This paragraph describes the process of calculating the mean, population variance, and standard deviation from a set of student scores. The mean is computed by summing all scores and dividing by the number of scores, resulting in a mean of 12. The population variance is then calculated using the formula \( \sigma^2 = \frac{\sum (x_i - \mu)^2}{N} \), where \( x_i \) represents each score, \( \mu \) is the mean, and \( N \) is the total number of scores. Each score is subtracted by the mean, squared, and summed up, then divided by the number of scores to find the variance, which is 21 in this case. The standard deviation is the square root of the variance, calculated to be 4.58.

05:02
📐 Final Values for Mean, Variance, and Standard Deviation

The second paragraph concludes the statistical calculations by presenting the final values for the mean, variance, and standard deviation. The mean of the student scores is reiterated as 12. The variance, calculated in the previous paragraph, is confirmed to be 21. The standard deviation, derived from the square root of the variance, is given as 4.58, providing a measure of the dispersion of the scores around the mean.

Mindmap
Keywords
💡Mean
The mean, also known as the average, is a measure of central tendency that represents the sum of all the values in a dataset divided by the number of values. In the video, the mean is calculated by adding all the student scores together and then dividing by the total number of scores (12 in this case), resulting in a mean of 12. This is a fundamental concept in statistics and is used to provide a single value that represents the entire dataset.
💡Population Variance
Population variance is a statistical measure that quantifies the dispersion of a set of data points in a population. It is calculated by taking the average of the squared differences from the Mean. In the script, the population variance is found by summing the squares of the differences between each score and the mean, then dividing by the number of scores (n=12). The variance is 21, indicating the spread of the student scores around the mean.
💡Standard Deviation
Standard deviation is a measure that is used to quantify the amount of variation or dispersion of a set of values. It is the square root of the variance and indicates the average distance of each data point from the mean. In the video, the standard deviation is calculated as the square root of the variance (21), which equals 4.58. This value helps in understanding the spread of the student scores in relation to the mean.
💡Scores
In the context of the video, scores refer to the numerical values representing the performance of students in a test or assessment. The script lists a series of scores (7, 11, 8, 8, 19, 15, 7, 9, 9, 20, 17, 14) which are used to calculate the mean, variance, and standard deviation. These scores are the raw data from which statistical measures are derived.
💡Summation
Summation is the mathematical operation of adding numbers together to find their total. In the video, the process of finding the mean involves summing all the student scores. The script mentions adding the scores (7+11+8+...+14) to get a total of 144, which is then used in the calculation of the mean.
💡Division
Division is the arithmetic operation of dividing one number by another. In the context of the video, division is used to calculate the mean by dividing the total sum of scores by the number of scores (144 divided by 12). It is also used in the calculation of variance, where the sum of squared differences is divided by the number of scores.
💡Squared
To square a number means to multiply the number by itself. In statistics, squaring is often used to eliminate negative values and to emphasize larger differences in data points. In the script, the differences between each score and the mean are squared (e.g., (-5)^2 = 25) before being summed for the calculation of variance.
💡Sample Variance
Sample variance is a statistical measure that estimates the population variance from a sample of data. Unlike population variance, which is calculated using the entire population (divided by n), sample variance is calculated using a sample of the data (divided by n-1). The script clarifies that the formula for population variance is used, which divides by n, not n-1.
💡Statistical Measures
Statistical measures are quantitative descriptions of a dataset that summarize its main characteristics. In the video, the mean, variance, and standard deviation are all examples of statistical measures. These measures provide insights into the central tendency and dispersion of the student scores.
💡Data Dispersion
Data dispersion refers to the spread of values within a dataset. It is an important aspect of understanding the variability of data. In the video, the variance and standard deviation are measures of dispersion, indicating how spread out the student scores are from the mean.
💡Contextualization
Contextualization in this video refers to the process of placing statistical terms and calculations within the context of the problem at hand, which is analyzing the scores of students. The script provides a step-by-step guide on how to apply these statistical concepts to a real-world scenario, making the abstract concepts more tangible and understandable.
Highlights

Introduction to the math problem involving calculating mean, population variance, and standard deviation using a table.

Given scores of students to find the mean by summing all scores and dividing by the number of scores.

Mean calculation result is 12 after adding individual scores and dividing by 12.

Explanation of the formula for calculating population variance, which differs from sample variance by using 'n' instead of 'n-1'.

Step-by-step calculation of 'x minus the mean' for each score to prepare for variance calculation.

Demonstration of squaring each 'x minus the mean' value as part of the variance formula.

Summation of the squared differences to find the submission for variance calculation.

Variance calculation by dividing the sum of squared differences by the number of scores (12).

Result of variance calculation is 21, indicating the dispersion of the scores around the mean.

Introduction to the concept of standard deviation as the square root of variance.

Calculation of standard deviation by taking the square root of the variance, resulting in 4.58.

Final results presented: mean is 12, variance is 21, and standard deviation is 4.58.

Emphasis on the importance of correctly identifying whether to use population or sample variance in statistical analysis.

Detailed walkthrough of the mathematical process, from summing scores to calculating mean, variance, and standard deviation.

Use of a table to organize and solve the statistical problem, showcasing a methodical approach.

Highlighting the mathematical operations involved in each step of the calculation process.

Clarification of the difference between squaring negative and positive numbers in the context of variance calculation.

Explanation of how to handle the sum of squared values in the variance formula.

Transcripts

Browse More Related Video

Variance and Standard Deviation: Sample and Population Practice Statistics Problems

Statistics: Standard deviation | Descriptive statistics | Probability and Statistics | Khan Academy

How to find the mean, median, mode, standard deviation and variance.

Measures of Dispersion (Ungrouped Data) | Basic Statistics

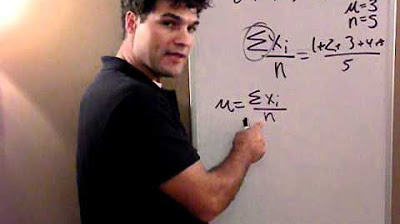
What is a "Standard Deviation?" and where does that formula come from

Find the Mean, Variance, & Standard Deviation of Frequency Grouped Data Table| Step-by-Step Tutorial

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsEducationStatisticsMean CalculationVarianceStandard DeviationData AnalysisEducational ContentStudent ScoresInteractive LearningMath Story