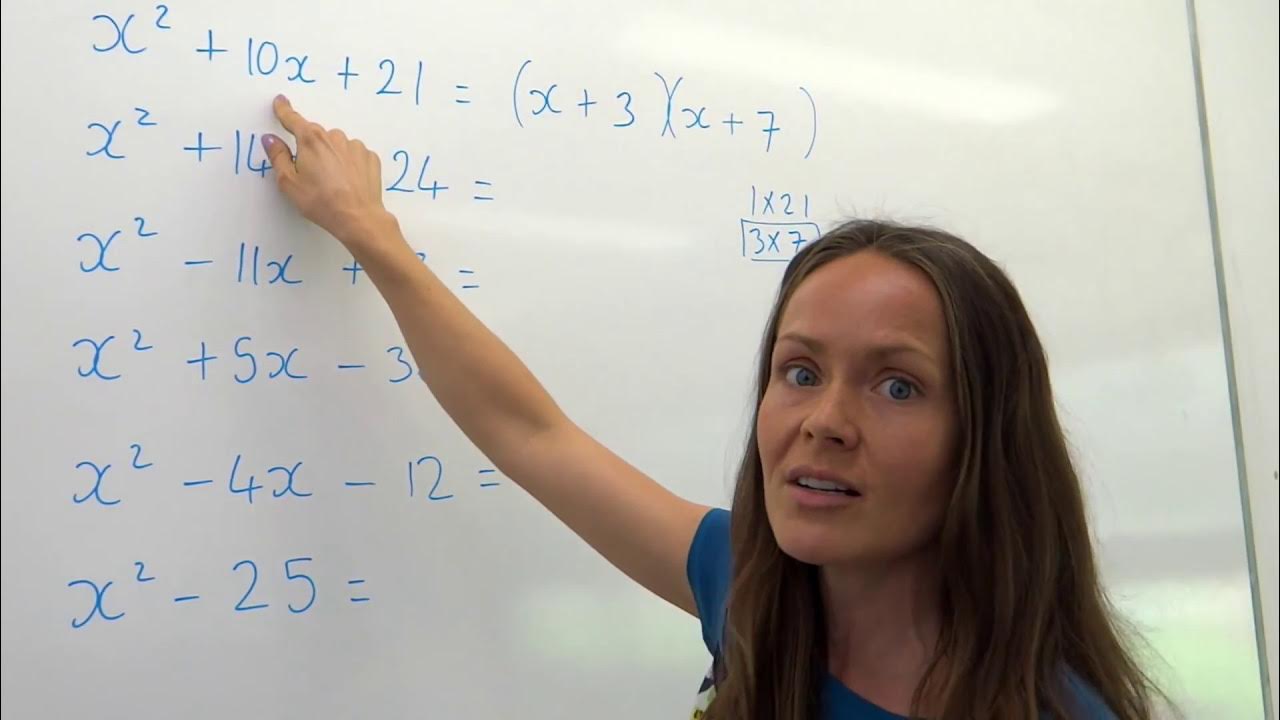GCSE Maths - Factorising Quadratics - Part 1 - (When the x^2 Coefficient is 1) - #50
TLDRThis video tutorial provides a step-by-step guide on how to factorize quadratic equations. It begins with an example, factorizing x^2 + 10x + 16, by identifying factor pairs of 16 that sum to 10. The method involves listing all factor pairs, both positive and negative, and then selecting the pair that adds up to the quadratic's middle coefficient. The process is repeated with a second example, x^2 + 5x - 14, to demonstrate the technique with a negative constant term. The video emphasizes the importance of a systematic approach for accuracy and efficiency, especially for more complex problems.
Takeaways
- 📚 The video is about teaching how to factorize quadratics, which involves rewriting a quadratic expression as two binomials multiplied together.
- 🔍 The example given is 'x squared plus 10x plus 16', which is to be factorized into two binomials with an 'x' in each.
- 📝 The first step is to identify all the factor pairs of the constant term (16 in this case), including both positive and negative pairs.
- ✅ It's important to list out all factor pairs on paper to avoid mistakes and to have a systematic approach, especially for more complex problems.
- 🔑 The next step is to find which factor pairs add up to the coefficient of the 'x' term (10 in the example), which helps in selecting the correct factors for the binomials.
- 🚫 Negative factor pairs are disregarded for the positive 'x' coefficient, focusing only on the positive pairs.
- 🔄 A trial and error process is used to find the correct pair that sums up to the 'x' coefficient.
- 📐 Once the correct factors are identified (2 and 8 in the example), they are placed in the binomials, resulting in '(x + 2)(x + 8)'.
- 🔍 To verify the factorization, the binomials are multiplied together to see if they yield the original quadratic expression.
- 📝 The process is repeated for a second example, 'x squared plus 5x minus 14', with a focus on factor pairs of the negative constant term.
- 🔄 For the second example, the correct factors that add up to the 'x' coefficient (5) are identified as -2 and 7, resulting in '(x - 2)(x + 7)'.
- 👍 The video concludes by encouraging viewers to practice this technique, emphasizing that it becomes easier with more examples.
Q & A
What is the main topic of the video?
-The main topic of the video is how to factorize quadratics, specifically teaching the process of rewriting a quadratic expression as two binomials multiplied together.
What is the first step in factorizing a quadratic according to the video?
-The first step is to write out two brackets with an 'X' in each one, preparing to factorize the quadratic into these two brackets.
Why is it important to write out all the factor pairs of the integer term in the quadratic?
-Writing out all the factor pairs helps to ensure that you consider all possible combinations that could potentially add up to the coefficient of the 'X' term in the quadratic.
What is the purpose of considering both positive and negative factor pairs for the integer term?
-Considering both positive and negative factor pairs is important because the integer term can be the result of either the sum or difference of two numbers, and the sign of the integer term dictates which combination to use.
How does the video suggest finding the correct pair of factors for the 'X' term in the quadratic?
-The video suggests using a process of trial and error to find which pair of factors adds together to make the coefficient of the 'X' term.
What is the method to verify if the factorization is correct?
-To verify the factorization, multiply the two brackets together and check if the result equals the original quadratic expression.
Why is it recommended to have a system in place for factorizing more complicated quadratics?
-A systematic approach helps to minimize errors and ensures a structured method for solving more complex quadratics, which is particularly useful in exam situations.
What is the example quadratic given in the video that is factorized first?
-The first example quadratic given in the video is 'x squared plus 10x plus 16'.
How does the video demonstrate the process of trial and error for finding the correct factors?
-The video demonstrates this by showing the process of adding the factors of 16 and checking if their sum equals the coefficient of 'X', which is 10 in the example.
What is the second example quadratic factorized in the video?
-The second example quadratic factorized in the video is 'x squared plus 5x minus 14'.
How does the sign of the integer term in the quadratic affect the selection of factor pairs?
-If the integer term is positive, only positive factor pairs are considered for the sum. If it's negative, factor pairs with at least one negative number are considered.
Outlines
📚 Factorizing Quadratics: A Step-by-Step Guide
This paragraph introduces the concept of factorizing quadratics, which involves rewriting a quadratic equation in the form of two binomials. The example given is x squared plus 10x plus 16, and the process begins by identifying factor pairs of the constant term (16) and finding which pair sums up to the coefficient of the linear term (10). The method emphasizes the importance of a systematic approach, especially for more complex quadratics, and concludes with verifying the factorization by multiplying the binomials to match the original quadratic.
🔍 Factorizing Quadratics with Negative Constant Terms
Continuing the discussion on factorizing quadratics, this paragraph focuses on a quadratic with a negative constant term, x squared plus 5x minus 14. The process involves listing factor pairs of -14, including both positive and negative combinations, and identifying the pair that sums to the linear coefficient (5). The correct pair, -2 and 7, is then placed into the binomials to complete the factorization. The paragraph wraps up with the factorized form of the quadratic and a reminder of the importance of this technique for solving more complex problems.
Mindmap
Keywords
💡Quadratic
💡Factorize
💡Binomials
💡Integer Term
💡Coefficient
💡Factor Pairs
💡Positive and Negative Factors
💡Trial and Error
💡Brackets
💡Verify
Highlights
Introduction to the process of factorizing quadratics.
Explanation of factorizing a quadratic equation like x squared plus 6x plus 8.
The goal of rewriting a quadratic as two multiplied brackets, representing factors of the original equation.
Starting with the example of factorizing x squared plus 10x plus 16.
Writing out two brackets with an 'X' in each as the initial step.
The importance of having a systematic approach for more complex quadratics.
Finding all factor pairs of the integer term (16 in this case).
Including both positive and negative factor pairs due to the positive nature of the integer term.
Listing all factor pairs and considering their sum to match the coefficient of the 'X' term.
Identifying the correct pair (2 and 8) that sums to the coefficient of 'X' (10).
Placing the correct numbers into the brackets to complete the factorization.
Verifying the factorization by multiplying the brackets and comparing to the original quadratic.
Demonstrating the process with another example: x squared plus 5x minus 14.
Writing out factor pairs for a negative integer term and considering the sum for the 'X' coefficient.
Selecting the pair that sums to the positive 'X' coefficient (5), which is -2 and 7.
Finalizing the factorization with the correct brackets and verifying the result.
Encouraging practice for ease and familiarity with the factorization technique.
Closing remarks and call to action for likes and subscriptions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: