Completing The Square Method and Solving Quadratic Equations - Algebra 2

The Organic Chemistry Tutor

15 Aug 201631:55

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script offers a comprehensive guide on solving quadratic equations through the method of completing the square. It walks viewers through various examples, demonstrating how to transform equations into perfect square trinomials, factor them, and find solutions, including real and imaginary numbers. The script simplifies complex expressions and encourages practice with additional problems, ensuring a clear understanding of the technique.

Takeaways

📚 The video focuses on solving quadratic equations by completing the square, a method that involves manipulating the equation to form a perfect square trinomial.
🔢 The first step in the process is often to isolate the quadratic and linear terms by moving the constant term to the other side of the equation.
🎯 To complete the square, find half of the coefficient of the linear term, square it, and add this value to both sides of the equation.
📐 After completing the square, the left side of the equation can be factored into a binomial squared, simplifying the process of finding the solution.
🤔 The technique is particularly useful for equations that are difficult to factor, including those with fractions or complex expressions.
📉 When the equation is not easily factorable, completing the square is a reliable alternative method to find the roots of the quadratic equation.
🤓 The video provides multiple examples to illustrate the process, including handling different scenarios such as when the equation cannot be factored.
🛑 If the completed square results in a negative number under a square root, the solutions involve imaginary numbers, indicated by 'i'.
📌 The script emphasizes the importance of simplifying expressions and working with common denominators when necessary.
📝 The process involves algebraic manipulation, including factoring, adding, and taking the square root of both sides of the equation.
📉 The video concludes with a summary that completing the square is a versatile method for solving quadratic equations, especially when factoring is not feasible.

Q & A

What is the first step to solve the equation x^2 + 4x + 3 = z by completing the square?
-The first step is to subtract 3 from both sides of the equation, resulting in x^2 + 4x = z - 3.
How do you find the number to add to both sides to complete the square for the equation x^2 + 4x?
-Take half of the coefficient of x, which is 4, and square it. Half of 4 is 2, and 2 squared is 4.
After adding the squared number to both sides, how can you factor the left side of the equation x^2 + 4x + 4?
-The left side factors into (x + 2)^2.
What is the next step after factoring the equation (x + 2)^2 = 1?
-Take the square root of both sides, resulting in x + 2 = ±1.
What are the solutions to the equation x + 2 = ±1?
-The solutions are x = -1 and x = -3.
How do you complete the square for the expression x^2 + 6x?
-Take half of 6, which is 3, and square it to get 9. Add 9 to both sides of the equation.
What is the factored form of the trinomial x^2 + 6x + 9?
-The factored form is (x + 3)^2.
What is the process to solve the equation x^2 - 6x - 9 by completing the square?
-Add 9 to both sides to get x^2 - 6x = 9, then add 9 to both sides again to complete the square, resulting in (x - 3)^2 = 18.
How can you simplify the square root of 18?
-The square root of 18 can be simplified to 3√2.
What are the steps to solve the equation 2x^2 - 8x + 9 = 0 by completing the square?
-Subtract 9 from both sides to get 2x^2 - 8x = -9, factor out the 2 to get 2(x^2 - 4x) = -9, complete the square inside the parentheses to get 2(x - 2)^2 = -1, divide by 2, and take the square root of both sides.

Outlines

00:00

📚 Introduction to Solving Quadratics by Completing the Square

This paragraph introduces the method of solving quadratic equations by completing the square. The first example given is X^2 + 4x + 3 = Z, where the equation is simplified by subtracting 3 from both sides. The process involves adding a specific number to both sides to form a perfect square trinomial, which is then factored into (x + 2)^2. The right side of the equation is adjusted accordingly, leading to the solution x = 1 or x = -3. The paragraph also mentions a technique for factoring expressions with fractions and provides additional examples.

05:01

🔍 Factoring and Completing the Square for Quadratic Equations

This paragraph discusses the process of factoring trinomials and when it is not possible, how to solve them by completing the square. An example of factoring is presented with the equation x^2 - 6x - 9, which factors into (x - 3)(x - 3). The paragraph then moves to an example where factoring is not possible, x^2 - 6x - 9, and demonstrates the completing the square method. The process involves adding 9 to both sides, adjusting the equation, and solving for x to find two decimal answers.

10:02

📝 Completing the Square with Different Coefficients

This paragraph explores completing the square with quadratic equations that have different coefficients. It starts with an example of x^2 - 8x + 10, which is modified to -8x + 10, and challenges the viewer to solve it. The solution involves subtracting 10 from both sides, adding 16 to both sides to complete the square, and then solving for x to find two decimal answers. The paragraph also discusses the case of no real solutions when the equation results in an imaginary number.

15:02

🔢 Solving Quadratics with Even Coefficients

This paragraph focuses on solving quadratic equations where all coefficients are even. The example x^2 + 8x - 8 = Z is simplified by dividing all terms by 2, resulting in x^2 + 4x - 4 = Z. The method of completing the square is then applied by adding 4 to both sides, factoring the left side, and solving for x to obtain two solutions involving square roots.

20:06

📉 Dealing with Imaginary Solutions in Quadratics

This paragraph addresses the scenario where completing the square results in an equation with no real solutions, specifically when the equation involves a negative number under a square root. The example 2x^2 - 8x + 9 is used to demonstrate this, leading to an imaginary solution expressed in terms of 'i', the imaginary unit. The process includes factoring out the coefficient, completing the square, and solving for x in terms of imaginary numbers.

25:06

🔄 Completing the Square with Fractional Coefficients

This paragraph demonstrates how to complete the square with quadratic equations that have fractional coefficients, such as 3x^2 - 5x - 7 = Z. The process involves factoring out the coefficient, finding half of the linear term's coefficient, squaring it, and adjusting the equation accordingly. The example concludes with solving for x, which results in an answer involving the square root of a fraction.

30:15

🎓 Final Practice Example and Conclusion

The final paragraph offers a practice example, 7x^2 + 5x - 8 = Z, and guides the viewer through the steps of solving it using the completing the square method. The process includes factoring out the coefficient, completing the square, and finding the square root of the resulting expression to solve for x. The paragraph concludes the video with a summary of the method and a thank you to the viewers.

Mindmap

Keywords

💡Quadratic Equations

Quadratic equations are polynomial equations of the second degree, typically in the form of ax^2 + bx + c = 0, where a, b, and c are constants. In the video's context, the theme revolves around solving these equations using a specific method. The script provides several examples of quadratic equations that are solved throughout the video, illustrating the process of finding their solutions.

💡Completing the Square

Completing the square is a method used to solve quadratic equations by transforming the quadratic expression into a perfect square trinomial plus a constant. The video focuses on this technique, demonstrating how to manipulate the equation to make the left side a square and then solve for the variable x. It is the central theme of the video, with each example showing a step-by-step application of this method.

💡Perfect Square Trinomial

A perfect square trinomial is an algebraic expression that can be factored into the square of a binomial. In the script, the term is used to describe the desired form of the quadratic equation after completing the square, such as (x + b/2a)^2. The video explains how to create a perfect square trinomial to facilitate the solution of the equation.

💡Factoring

Factoring is the process of breaking down a polynomial into a product of its factors. In the context of the video, factoring is used as an alternative method to solve certain quadratic equations when possible. The script mentions that not all trinomial expressions can be factored, but when they can, it provides a simpler way to find the solutions for x.

💡Square Root

The square root operation is used to find a number that, when multiplied by itself, gives the original number. In the video, taking the square root is a step in the process of solving for x after completing the square. The script provides examples where the square root is applied to both sides of the equation to isolate x and find its value.

💡Imaginary Numbers

Imaginary numbers are a concept in mathematics where the square root of a negative number is considered valid. In the script, the term is introduced when the square of a negative number cannot be simplified into a real number, leading to the use of 'i' to represent the square root of -1. The video explains that while some equations may not have real solutions, they can have imaginary solutions.

💡Rationalizing the Denominator

Rationalizing the denominator is a process used to eliminate the radical (or imaginary unit) from the denominator of a fraction. The video script mentions this process when dealing with the square root of 18, which is simplified by breaking it down into the square root of 9 times the square root of 2, and then simplifying the square root of 9 to 3.

💡Common Denominator

A common denominator is a denominator that is the same for two or more fractions, allowing them to be added or subtracted. In the script, finding a common denominator is part of the process when combining terms with different denominators, such as when adding 8/28 and 25/28 to get 249/28.

💡Simplifying Radicals

Simplifying radicals involves breaking down a radical expression into its simplest form. The video script demonstrates this when it simplifies the square root of 18 into 3 times the square root of 2, showing the process of reducing the complexity of the radical expression.

💡Decimal Form

Decimal form is a way of expressing numbers using digits to the right of a decimal point. In the script, converting answers into decimal form is mentioned as a way to express the solutions for x when the square root cannot be simplified into a whole number, providing a more precise answer.

Highlights

Introduction to solving quadratic equations by completing the square.

Starting example with the equation x^2 + 4x + 3 = z.

Subtracting 3 from both sides to form x^2 + 4x = 3.

Adding 2^2 to both sides to form a perfect square trinomial.

Factoring x^2 + 4x + 4 as (x + 2)^2.

Solving the resulting equation (x + 2)^2 = 1 by taking the square root of both sides.

Writing two equations from the square root: x + 2 = 1 and x + 2 = -1.

Solving for x to find the roots: x = -1 and x = -3.

Applying the same method to a different example x^2 + 6x.

Adding 3^2 to both sides and factoring to (x + 3)^2.

Discussion on how to solve by completing the square when trinomials cannot be factored.

Example of solving x^2 - 6x - 9 by completing the square.

Adding 9 to both sides and forming (x - 3)^2.

Simplifying the square root of a non-perfect square (e.g., 18).

Handling equations with fractions and imaginary numbers using the method.

Transcripts

Browse More Related Video

Factoring Trinomials & Polynomials, Basic Introduction - Algebra

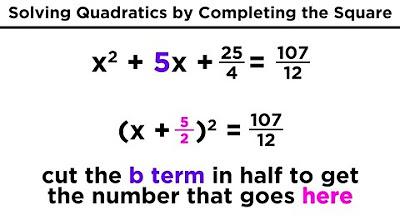
Solving Quadratics by Completing the Square

How To Find The Real & Imaginary Solutions of Polynomial Equations

How to solve quadratic equations (by factoring, completing the square, & quadratic formula)

Add, Subtract, Multiply, Divide Imaginary & Complex Numbers - [1]

How To Use The Quadratic Formula To Solve Equations

Related Tags

Quadratic Equations Math Tutorial Completing the Square Step-by-Step Algebra Math Help Education Learning Math Examples Student Guide