Factoring Trinomials & Polynomials, Basic Introduction - Algebra
TLDRThis educational video script offers a comprehensive guide on factoring techniques in algebra. It covers identifying the greatest common factor (GCF), factoring by grouping, and solving equations through factoring. The script also explains how to factor trinomials, perfect square trinomials, difference of squares, and sums and differences of cubes. Additionally, it demonstrates solving equations by applying the zero product property and factoring complex expressions involving perfect squares and cubes, providing clear examples to aid understanding.
Takeaways
- 📚 The video covers various methods of factoring, including finding the greatest common factor (GCF) and factoring by grouping.
- 🔢 To factor by GCF, identify the largest number that divides evenly into all terms of the expression, and simplify the expression by dividing each term by the GCF.
- 📉 The script explains how to factor binomials and polynomials with more than two terms, such as 4x^2 + 8x and x^3 - 4x^2 + 3x - 12.
- 📈 For expressions with variables and coefficients, choose the GCF considering both numerical coefficients and variable factors, as shown in examples like 5x^2 - 15x^3.
- 📝 Factoring by grouping is demonstrated with a step-by-step approach, showing how to break down expressions into groups and factor out the GCF from each group.
- 🔍 The video teaches how to identify and factor perfect square trinomials, which are of the form a^2 + 2ab + b^2, and can be factored into (a + b)^2.
- 📐 The script also covers the factoring of difference of squares, which follows the formula a^2 - b^2 = (a + b)(a - b).
- 🆚 Difference and sum of cubes are explained with their respective formulas, a^3 + b^3 = (a + b)(a^2 - ab + b^2) and a^3 - b^3 = (a - b)(a^2 + ab + b^2).
- 📚 The process of solving equations by factoring is discussed, using the zero product property which states that if the product of two factors is zero, at least one of the factors must be zero.
- 📉 Examples are provided to illustrate solving equations, such as 6x^2 - 30x = 0, by factoring and applying the zero product property to find the values of x.
- 📝 The video script concludes with a more complex example involving a combination of perfect square trinomials and difference of squares, showing how to factor and solve for variables.
Q & A
What is the Greatest Common Factor (GCF) of the expression 3x + 15?
-The GCF of 3x + 15 is 3, as both terms are divisible by 3.
How do you factor the expression 7x - 28 by removing the GCF?
-Both 7x and -28 are divisible by 7. Dividing each term by 7 gives x - 4, so the factored form is 7(x - 4).
What is the GCF of 4x^2 + 8x, and how do you factor it?
-The GCF of 4x^2 + 8x is 4x. Factoring out 4x gives x(4x + 8), which simplifies to x(2 + 4).
In the expression 5x^2 - 15x^3, what is the GCF and how do you factor it?
-The GCF of 5x^2 and -15x^3 is 5x^2. Dividing each term by 5x^2 gives 1 and -3x, so the factored form is 5x^2(1 - 3x).
How do you verify if your factoring is correct?
-You can verify your factoring by multiplying the factors together to see if you get the original expression.
What is the process for factoring by grouping in a polynomial with four terms?
-For factoring by grouping, separate the polynomial into two parts, factor out the GCF from each part, and then look for a common binomial factor between the two groups to combine them into a single expression.
How can you determine if a trinomial is a perfect square trinomial?
-A trinomial is a perfect square trinomial if it is in the form a^2 + 2ab + b^2, and the square root of the first term times the square root of the last term, multiplied by two, equals the middle term.
What is the difference of squares formula for factoring?
-The difference of squares formula is a^2 - b^2 = (a + b)(a - b).
How do you factor a perfect square trinomial that is not easily recognizable?
-For perfect square trinomials that are not easily recognizable, you can use the equation (a + b)^2 = a^2 + 2ab + b^2 to identify the terms and factor accordingly.
What is the process for solving an equation by factoring?
-To solve an equation by factoring, first factor the equation if possible. Then, use the zero product property, which states that if the product of two factors is zero, then at least one of the factors must be zero. Set each factor equal to zero and solve for the variable.
How do you solve the equation 6x^2 - 30x = 0 using factoring?
-Factor out the GCF, which is 6x, to get 6x(x - 5) = 0. Then, apply the zero product property to find x = 0 or x = 5.
Outlines
📚 Introduction to Factoring by GCF
This paragraph introduces the concept of factoring by finding the greatest common factor (GCF). It explains how to factor expressions such as 3x + 15 and 7x - 28 by dividing each term by their GCF, which are 3 and 7 respectively. The paragraph also presents additional examples including 4x^2 + 8x and 5x^2 - 15x^3, illustrating the process of factoring by removing the GCF and simplifying the expressions. The importance of checking work by multiplying the factors is emphasized.
🔍 Factoring by Grouping
The second paragraph delves into the method of factoring by grouping, a technique used for polynomial expressions with four terms. It uses the example of x^3 - 4x^2 + 3x - 12 to demonstrate how to separate the expression into two groups, factor out the GCF from each group, and then combine like terms to rewrite the expression in factored form. Another example, 2r^3 - 6r^2 + 5r - 15, is provided for practice, highlighting the importance of identifying a common term to successfully factor by grouping.
🔢 Factoring Trinomials with a Leading Coefficient of 1
This section focuses on factoring trinomials where the leading coefficient is 1. It provides a step-by-step guide on finding two numbers that multiply to the constant term and add up to the linear coefficient. Examples include factoring expressions like x^2 + 7x + 12 into (x + 3)(x + 4) and x^2 + 3x - 20 into (x + 7)(x - 4). The process involves listing factors of the constant term and identifying pairs that sum to the linear coefficient.
📉 Factoring Trinomials with a Non-Unit Leading Coefficient
The paragraph discusses how to factor trinomials when the leading coefficient is not 1. It suggests multiplying the leading coefficient by the constant term and finding two numbers that multiply to this product and add up to the linear coefficient. An example is given with the expression 2x^2 - 9x + 20, which is factored by first factoring out the GCF of 2 and then using the technique described to factor the remaining quadratic expression.
📈 Factoring Perfect Square Trinomials and Difference of Squares
This part of the script covers the factoring of perfect square trinomials and the difference of squares. It explains that a perfect square trinomial is of the form a^2 + 2ab + b^2 and can be factored into (a + b)^2. The difference of squares, a^2 - b^2, can be factored into (a + b)(a - b). Examples are provided to illustrate the identification of perfect square trinomials and the application of the respective formulas for factoring.
📊 Factoring Sum and Difference of Cubes
The script explains the factoring of sums and differences of cubes, providing the formulas for each: sum of cubes a^3 + b^3 factors into (a + b)(a^2 - ab + b^2), and difference of cubes a^3 - b^3 factors into (a - b)(a^2 + ab + b^2). It includes examples demonstrating the process of identifying cubes and applying the formulas to factor expressions like x^3 + 8 and 8x^3 - 27.
📝 Solving Equations by Factoring
The final paragraph of the script discusses solving equations by factoring. It starts with a simple example of a binomial equation 6x^2 - 30x = 0, showing how to factor out the GCF and use the zero product property to find the values of x. Further examples are given, including solving 3x^2 - 27 and x^2 - 5x - 36 by factoring and applying the zero product property to determine the solutions for x.
Mindmap
Keywords
💡Factoring
💡Greatest Common Factor (GCF)
💡Binomial
💡Polynomial
💡Factor by Grouping
💡Trinomial
💡Perfect Square Trinomial
💡Difference of Squares
💡Sum and Difference of Cubes
💡Zero Product Property
Highlights
Introduction to factoring by finding the Greatest Common Factor (GCF).
Demonstration of factoring the expression 3x + 15 by identifying 3 as the GCF.
Example of factoring 7x - 28 by dividing by the GCF, which is 7.
Factoring the expression 4x^2 + 8x by taking out the GCF of 4x.
Explanation of factoring trinomials with the leading coefficient of 1.
Technique for factoring by grouping with a polynomial expression of four terms.
Process of factoring a trinomial when the leading coefficient is not 1.
Identification of perfect square trinomials and their factoring method.
Difference of squares factoring and its application in expressions.
Introduction to factoring sums and differences of cubes with formulas.
Solving equations by factoring and using the zero product property.
Method for solving equations with a difference of perfect squares.
Approach to factoring expressions that are sums and differences of cubes.
Strategy for dealing with expressions that include both perfect square trinomials and difference of squares.
Advanced example of solving a complex equation involving perfect squares and cubes.
Final summary of the techniques learned for factoring various types of algebraic expressions.
Transcripts
Browse More Related Video

How To Factor Polynomials The Easy Way!

Factoring Polynomials - By GCF, AC Method, Grouping, Substitution, Sum & Difference of Cubes

Factoring Review

How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
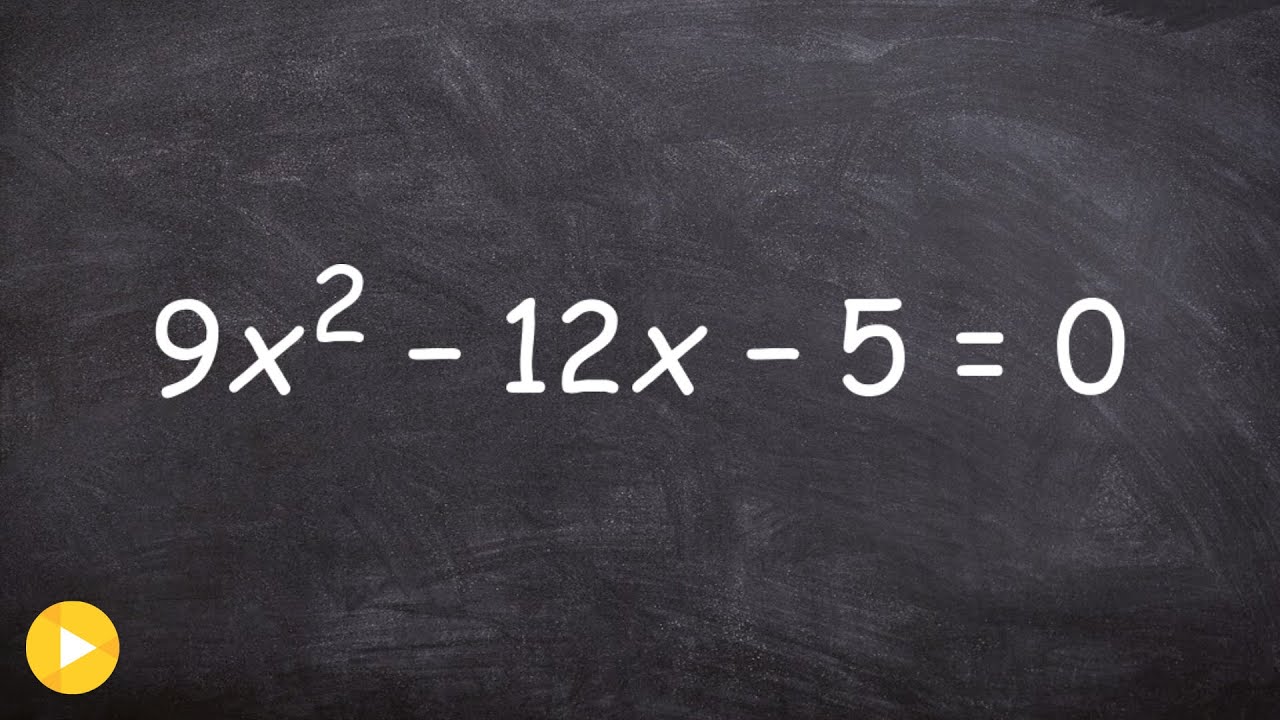
Learn the ac method for factoring and solving a quadratic equation

Follow this tip when factoring by grouping
5.0 / 5 (0 votes)
Thanks for rating: