Follow this tip when factoring by grouping

Brian McLogan
21 Dec 202305:53
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter highlights a common mistake students make when factoring by grouping: incorrectly grouping terms and creating multiplication problems instead. The key tip is to change subtraction to addition to avoid this error. The video demonstrates how to correctly group terms, factor out the greatest common factor (GCF), and check work for accuracy. It concludes with applying the difference of two cubes formula for complete factorization, ensuring students can avoid the typical pitfalls in algebraic factoring.

Takeaways
  • 📚 Factoring by grouping is a common method for polynomials with four terms.
  • 🔍 Arrange terms in descending order to prepare for factoring by grouping.
  • ❌ Avoid incorrect grouping by not creating a multiplication problem with parentheses.
  • 🔄 Change subtraction to addition to simplify the process of factoring by grouping.
  • 📝 Remember that 5 - 4 is the same as 5 + (-4), which helps in rearranging terms.
  • 👉 Group the first two terms and the last two terms, ensuring operations are not altered.
  • 📉 Factor out the greatest common factor (GCF) to simplify expressions.
  • 🔍 After factoring out the GCF, check that the remaining expressions are the same to ensure correct factoring.
  • 📌 Look for the difference of cubes pattern if you have a cubic term minus another cubic term.
  • 📘 Apply the formula for the difference of cubes (a^3 - b^3 = (a - b)(a^2 + ab + b^2)) to further factor the expression.
  • 🎯 After fully factoring, verify your work by multiplying the factors back to the original expression.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is to demonstrate a common mistake students make when factoring by grouping and to provide a tip to avoid this mistake.

  • What is the first step when factoring by grouping?

    -The first step is to group the first two terms and the last two terms of a polynomial with four terms.

  • Why is it important to arrange terms in descending order when factoring by grouping?

    -Arranging terms in descending order helps to ensure that the terms are grouped correctly and that the operations are not changed during the factoring process.

  • What is the common mistake students make when adding parentheses during factoring by grouping?

    -The common mistake is creating a multiplication problem by adding parentheses, which changes the operations and leads to an incorrect factoring.

  • What is the rule suggested in the video to avoid the mistake of changing operations during factoring by grouping?

    -The rule is to change a subtraction problem to an addition problem by adding a negative to the terms, which allows for correct grouping without changing the operations.

  • How does changing from a subtraction to an addition help in factoring by grouping?

    -Changing to an addition allows for the terms to be grouped without altering the operations, making it possible to factor by grouping correctly.

  • What is the purpose of factoring out the greatest common factor (GCF)?

    -Factoring out the GCF simplifies the expression and makes it easier to identify common terms that can be factored out further.

  • How can you check if your factoring by grouping is correct?

    -You can check by multiplying the factored terms back to see if they match the original expression.

  • What is the difference of two cubes formula mentioned in the video?

    -The difference of two cubes formula is a^3 - b^3 = (a - b)(a^2 + ab + b^2).

  • Why is it important to ensure that the expressions left after factoring out the GCF are the same?

    -Ensuring the expressions are the same confirms that the factoring is correct and allows for further factoring, such as applying the difference of two cubes formula.

  • What is the final step in the video after factoring out the common terms?

    -The final step is to apply the difference of two cubes formula if applicable, to completely factor the polynomial.

Outlines
00:00
📚 Mastering Factoring by Grouping: Common Mistakes and Tips

This paragraph discusses a common mistake students make when factoring by grouping, which involves polynomials with four terms. The instructor emphasizes the importance of arranging terms in descending order and cautions against incorrect grouping that leads to multiplication problems. The key tip is to change subtraction to addition when there's a negative sign between terms, allowing for proper grouping without altering the equation's meaning. The summary also includes a step-by-step demonstration of factoring out common terms like x cubed and checking work by ensuring the remaining expressions are identical after factoring out the greatest common factor (GCF).

05:02
🧩 Applying the Difference of Cubes Formula for Complete Factorization

The second paragraph focuses on the application of the difference of cubes formula to fully factor a polynomial. It explains the recognition of cube numbers within the expression and the use of the formula a^3 - b^3 = (a - b)(a^2 + ab + b^2) to rewrite the expression in factored form. The instructor guides through identifying 'a' and 'b' as the cube roots of the respective terms, demonstrates the factorization process, and encourages viewers to watch the next video for further understanding of factoring by grouping techniques.

Mindmap
Keywords
💡Factoring by Grouping
Factoring by Grouping is a mathematical technique used to simplify polynomials with four terms. It involves grouping the first two terms and the last two terms of the polynomial and factoring out the greatest common factor (GCF) from each group. In the video, this method is the main focus, and the instructor discusses common mistakes students make while applying it, such as incorrectly adding parentheses which changes the multiplication problem into an incorrect one.
💡Polynomial
A polynomial is an algebraic expression consisting of variables and coefficients, involving only the operations of addition, subtraction, and multiplication, and non-negative integer exponents of variables. The video script discusses polynomials with four terms, which are the subject of the factoring by grouping technique.
💡Greatest Common Factor (GCF)
The Greatest Common Factor, or GCF, is the largest factor that two or more numbers share. In the context of the video, the GCF is factored out from each group of terms in a polynomial to simplify the expression. The script provides an example of factoring out 'x cubed' as the GCF from the given polynomial.
💡Descendant Order
Descendant order refers to the arrangement of terms in a polynomial from the highest to the lowest degree. The script mentions that terms should be arranged in descending order when factoring by grouping, which helps in identifying and grouping like terms correctly.
💡Common Mistake
The term 'common mistake' in the script refers to the errors students often make while factoring by grouping, such as incorrectly adding parentheses which changes the nature of the problem. The video aims to educate students on how to avoid these mistakes.
💡Multiplication Problem
A multiplication problem in the script refers to the incorrect formation of a polynomial expression when students add parentheses incorrectly during factoring by grouping. This changes the expression from a sum to a product, which is not the intended outcome of the factoring process.
💡Addition Problem
An addition problem in the context of the video is a correctly formed polynomial expression where terms are added together. The instructor suggests changing a subtraction to an addition to correctly group terms for factoring, as seen when changing '-27x' to '+(-27x)'.
💡Difference of Two Cubes
The Difference of Two Cubes is a specific algebraic identity that states a^3 - b^3 can be factored into (a - b)(a^2 + ab + b^2). In the script, the instructor uses this identity to further factor the expression after applying factoring by grouping, showing how to identify and apply this rule.
💡Cube Root
The cube root of a number is a value that, when multiplied by itself three times, gives the original number. In the video, the cube root is used to identify the base values 'a' and 'b' for applying the difference of two cubes formula, with examples like the cube root of x cubed being x, and the cube root of 27 being 3.
💡Checking Work
Checking work in the script refers to the process of verifying the correctness of the factoring steps by multiplying the factors back to ensure they yield the original polynomial. The instructor emphasizes this as a good practice to ensure accuracy in mathematical problem-solving.
💡Factored Form
Factored form is the result of expressing a polynomial as a product of its factors. In the video, the instructor demonstrates how to reach the factored form of the given polynomial through a series of steps, including factoring by grouping and applying the difference of two cubes.
Highlights

The video aims to show a top mistake students make when factoring by grouping and provides a tip to avoid it.

Students are advised to consider factoring by grouping when they see a polynomial with four terms.

The importance of arranging terms in descending order for factoring by grouping is emphasized.

A common mistake is incorrectly grouping terms by adding parentheses, which changes the multiplication problem.

Another mistake is changing the sign incorrectly when grouping terms around a negative sign.

The correct method is to change a subtraction problem to an addition problem to facilitate proper grouping.

The video explains how to group terms correctly by changing the operation between terms.

Factoring by grouping is demonstrated with an example, including factoring out the greatest common factor (GCF).

A tip for checking work after factoring out the GCF is provided.

The necessity of ensuring that the expressions left after factoring out are the same is discussed.

The video demonstrates how to correct mistakes in the factoring process and verify the results.

The difference of two cubes formula is introduced as a method to further factor the expression.

The process of identifying 'a' and 'b' in the difference of two cubes formula is explained.

The final step of completely factoring the polynomial using the difference of two cubes is shown.

The video concludes with a summary of how to avoid common mistakes in factoring by grouping.

An invitation to watch the next video for more information on factoring by grouping is extended.

Transcripts

Browse More Related Video

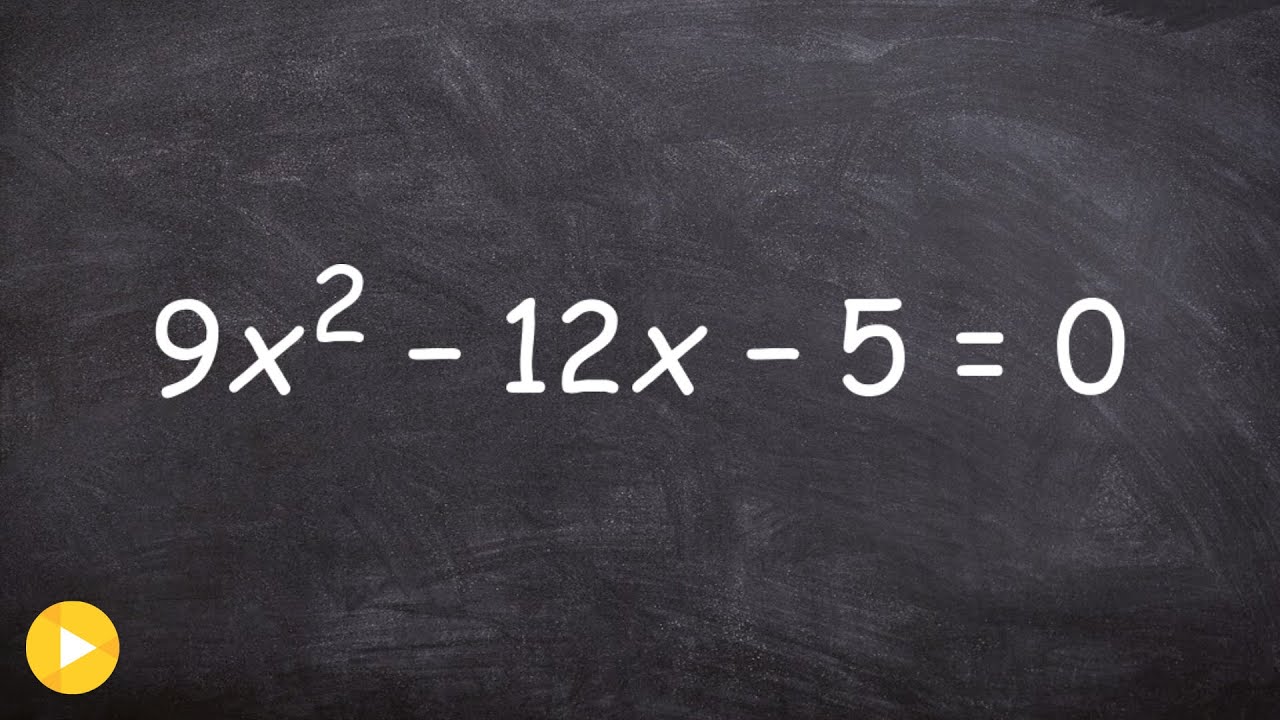
Learn the ac method for factoring and solving a quadratic equation

Factoring Trinomials & Polynomials, Basic Introduction - Algebra

Factoring Review

Factoring Polynomials - By GCF, AC Method, Grouping, Substitution, Sum & Difference of Cubes

How To Factor Polynomials The Easy Way!

Ch. 1.3 Algebraic Expressions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Factoring TipsAlgebra MistakesGrouping MethodMath EducationPolynomial FactoringCommon ErrorsAlgebraic TechniquesStudent GuidanceMath StrategiesEducational Content