AP Calculus Practice Exam Part 4 (MC #76-83)

Hittin' the Board with Mr. Vranderic
18 Apr 202310:30
EducationalLearning
32 Likes 10 Comments

TLDRThis video script covers an AP Calculus practice test, focusing on concepts such as the use of derivatives to determine intervals of increase/decrease and concavity, calculating velocity from a height function, linear approximation, and average heart rate. It also discusses the Fundamental Theorem of Calculus for definite integrals, types of discontinuities, and solving integrals using technology. The instructor emphasizes the importance of understanding these concepts and applying them to solve multi-choice questions efficiently.

Takeaways
  • 📈 The script discusses the application of the first and second derivative tests to determine the intervals where a function is increasing or concave up and down.
  • 🔍 For question 76, the focus is on identifying intervals where the derivative of a function is positive, indicating where the original function is increasing.
  • ⏱ In question 77, the process involves finding the velocity of an object at a specific time by taking the derivative of the height function and evaluating it at that time.
  • 📚 Question 78 introduces linear approximation, which is calculated by using the derivative of a function at a known point and the distance from that point to the unknown.
  • 💓 The average heart rate in question 79 is found by integrating the heart rate function over a given interval and dividing by the length of the interval.
  • 🧩 Question 80 examines the Fundamental Theorem of Calculus, Part 2, which is used to evaluate the definite integral and find the value of a function at a specific point.
  • 🔄 The script mentions removable discontinuity in question 81, which is characterized by a 'hole' in the function that can be 'moved' to make the function continuous.
  • 🔢 In question 82, the solution involves breaking down the problem into parts and using known integrals to solve for an unknown integral.
  • 📊 For question 83, the script suggests using graphing technology to find the intersection points of two functions to determine the value of a variable.
  • 🛠️ The script emphasizes the utility of calculators in solving calculus problems, especially when dealing with complex integrals and derivatives.
  • 📝 The transcript is a guide for students taking an AP Calculus practice test, highlighting the importance of understanding calculus concepts and the application of technology in problem-solving.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is practicing AP Calculus problems, focusing on understanding the behavior of functions, derivatives, and integrals, as well as utilizing a calculator for solving these problems.

  • How does the script define an increasing function in the context of the first derivative?

    -In the script, an increasing function is defined as one where the first derivative is positive. This means that wherever the y-values of the derivative graph are positive, the original function is increasing.

  • What is the process described for finding the velocity of an object at a specific time?

    -The process involves taking the derivative of the height function, which represents the position of the object. Then, plugging in the specific time (T equals 3 in the script) into this derivative to find the velocity at that moment.

  • What is linear approximation and how is it used in the script?

    -Linear approximation is a method used to estimate the value of a function at a point near a known value. In the script, it is used to find the approximation for G of negative 1.2 by using the derivative evaluated at the nearest known point (G of negative 1) and the difference from that point.

  • How is the average heart rate calculated in the script?

    -The average heart rate is calculated as the average value of a function over a given interval. The formula used is (1/(B-A)) * integral from A to B of the function H(t), where A and B are the time intervals in minutes.

  • What is the Fundamental Theorem of Calculus Part 2, and how is it applied in the script?

    -The Fundamental Theorem of Calculus Part 2 states that the definite integral of a function can be found by evaluating the antiderivative of the function at the upper and lower limits of integration. In the script, it is used to find the value of G of 5 by integrating G'(x) from 2 to 5 and then adjusting for the known value of G at 2.

  • What are the three types of discontinuity mentioned in the script?

    -The three types of discontinuity mentioned are removable (like a hole that can be 'moved'), jump discontinuity (where the function has a jump), and infinite discontinuity (where the function approaches infinity, often associated with asymptotes).

  • How does the script approach the problem of finding the value of an integral with four pieces, knowing three of them?

    -The script suggests setting up the equation based on the known values and solving for the unknown piece. It uses the method of breaking down the integral into known parts and then solving for the missing part by equating it to the sum of the known parts.

  • What is the strategy used in the script to determine if a value of k makes the equation true?

    -The strategy involves graphing the functions and looking for intersections at the point where the equation should hold true (x equals 3 in the script). If an intersection is found at that point, it indicates the value of k makes the equation true.

  • What does the script suggest if none of the provided values for k work out?

    -If none of the provided values for k work out, the script suggests typing in the next values and checking for intersections. If all values fail to produce an intersection at the required point, the answer would be 'no such value' or 'D' as indicated in the script.

Outlines
00:00
📈 Understanding Derivatives for Function Behavior

This paragraph discusses the use of derivatives to determine the intervals on which a function is increasing or decreasing. It explains that a positive first derivative indicates an increasing function and a negative one indicates a decreasing function. The speaker also covers the concept of concavity and how it relates to the second derivative. The example involves analyzing a given graph to identify intervals of increase from 0 to 2 and from 4 to 5.

05:00
🚀 Calculating Velocity and Linear Approximation

The speaker provides a step-by-step explanation of how to find the velocity of an object at a specific time by taking the derivative of the height function. The example involves calculating the velocity at time T equals 3 using the power rule and a calculator to find the derivative. Additionally, the paragraph covers the process of linear approximation, where the speaker uses known values to approximate the value of a function at a nearby point, without the need for a calculator.

10:03
📊 Analyzing Average Heart Rate and Fundamental Theorem of Calculus

This section covers the calculation of the average value of a function over a given interval, using the integral and the formula for average value. The speaker applies this to find the average heart rate between 30 and 60 minutes. The paragraph also discusses the fundamental theorem of calculus, specifically part two, which is used to evaluate definite integrals. An example is given where the speaker calculates the value of a function at a specific point by evaluating the integral of its derivative from two points and adjusting for known values.

🔍 Identifying Types of Discontinuity and Intersection Points

The final paragraph delves into the concept of discontinuity, explaining the three types: removable, jump, and infinite. The speaker identifies a removable discontinuity in the given example. The paragraph also describes a method for finding intersection points of two functions using graphing technology, which simplifies the process compared to algebraic methods. The speaker demonstrates this by graphing two functions and using the intersection feature to find the exact point where they meet.

Mindmap
Keywords
💡First Derivative
The first derivative of a function represents the rate of change or the slope of the tangent line to the curve of the function at a given point. In the video, it is used to determine where the original function is increasing or decreasing. For instance, when the derivative is positive, the function is increasing, as explained in the context of question 76.
💡Second Derivative
The second derivative is the derivative of the first derivative and provides information about the concavity of a function. It indicates whether the function is concave up or down. In the script, the second derivative is used to understand the concavity of the function, which is crucial for analyzing the shape of the graph in the context of the AP calculus practice test.
💡Continuous Function
A continuous function is one where there are no breaks or jumps in the graph. In the video, the function is described as continuous on a closed interval, which is essential for analyzing the behavior of the function and its derivatives over that interval, as seen in the discussion of question 76.
💡Velocity
Velocity is a measure of the rate of change of an object's position with respect to time. In the context of the video, the script discusses finding the velocity of an object at a specific time by taking the derivative of the height function, illustrating the concept with the formula 2T plus 16T to the negative second power, where T equals 3.
💡Linear Approximation
Linear approximation is a method used to estimate the value of a function at a point using the tangent line at a nearby known point. In the script, the concept is applied to find an approximation for G of negative 1.2 by using the derivative at G of negative 1 and the difference between the points, resulting in an approximation of 3.6.
💡Average Heart Rate
The average heart rate in the script refers to the average value of a function over a given interval, calculated using the formula for the average value of a continuous function. The video explains how to find the average heart rate from 30 to 60 minutes by integrating the function H(t) over that interval and comparing it to the answer choices provided.
💡Fundamental Theorem of Calculus Part Two
This theorem allows for the evaluation of definite integrals by finding the difference in the values of an antiderivative at the bounds of integration. In the video, it is used to find the value of G of 5 by setting up an integral from 2 to 5 of G'(x) and then subtracting G of 2 from the result, as demonstrated in the explanation of question 80.
💡Removable Discontinuity
A removable discontinuity occurs at a point on the graph where the function is not defined but could be made continuous by redefining the function's value at that point. The script mentions this type of discontinuity in the context of question 81, where the option C is identified as having a removable discontinuity, akin to a hole in the graph that can be 'moved' elsewhere.
💡Integral
An integral in calculus represents the area under the curve of a function over an interval. The script discusses integrals in the context of summing areas to find a total, such as the integral from 0 to 17 of f(x) plus the integral from 17 to 20, which is equivalent to the integral from 0 to 13 plus the integral from 13 to 20, as explained in question 82.
💡Intersection
The intersection of two curves is the point or points where both curves meet or touch. In the script, the concept is used to determine if a certain value of k makes two equations continuous at x equals 3 by graphing and finding the intersection point, which is approximately 3, indicating the value of k works.
Highlights

Use of calculators is allowed in the AP calculus practice test.

Explanation of how the first derivative indicates the increasing intervals of a function.

Understanding second derivative values to determine concavity of a function.

Calculation of velocity at time T equals 3 using the derivative of height function.

Derivation of the formula for linear approximation and its application.

Explanation of the average heart rate calculation using the integral of a function.

Application of the fundamental theorem of calculus part two to find the value of a definite integral.

Technique for finding the value of G of 5 using the integral of G prime of X.

Identification of removable discontinuity in a function.

Approach to solving integrals by breaking them into known segments.

Technique for solving for an unknown integral value by comparing known segments.

Utilization of technology to graph and find intersections for algebraic solutions.

Method for verifying the continuity of a function by graphing and finding intersections.

Use of calculator technology to quickly check potential values for a given algebraic condition.

Process of eliminating incorrect values systematically to find the correct solution.

Conclusion of the first part of the practice test with an invitation to return for the second part.

Transcripts

Browse More Related Video

AP Calculus BC Practice Exam 2012 - Calculator Multiple Choice questions 76-92

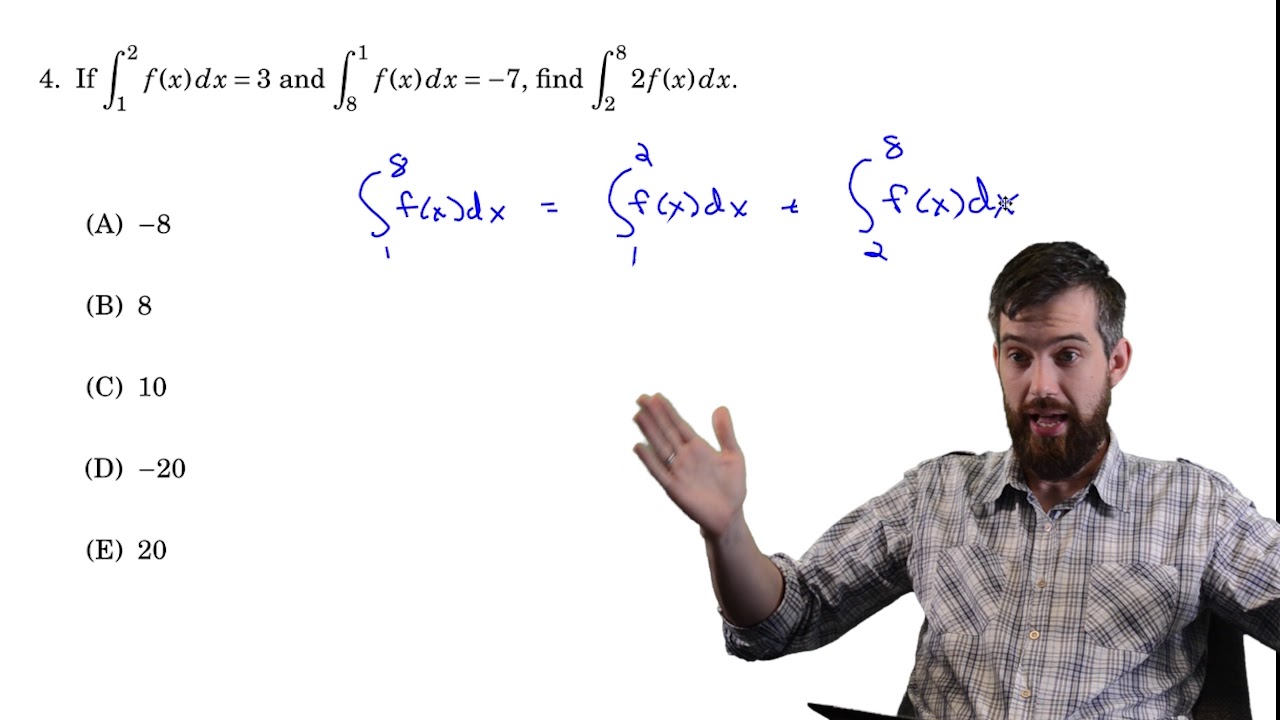
Exam Walkthrough | Calc 1, Test 3 | Integration, FTC I/II, Optimization, u-subs, Graphing

AP Calculus AB 1998 Multiple Choice No Calculator

AP Calculus AB 2003 Multiple Choice (no calculator) - Questions 1-28

Math Test Practice Test [ 30 Minutes ] Math for Business and Economics

AP Calc AB & BC Practice MC Review Problems #5

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus PracticeDerivativesIntegralsAP CalcTest PrepEducationalMathematicsGraph AnalysisFunction StudyConcept Review