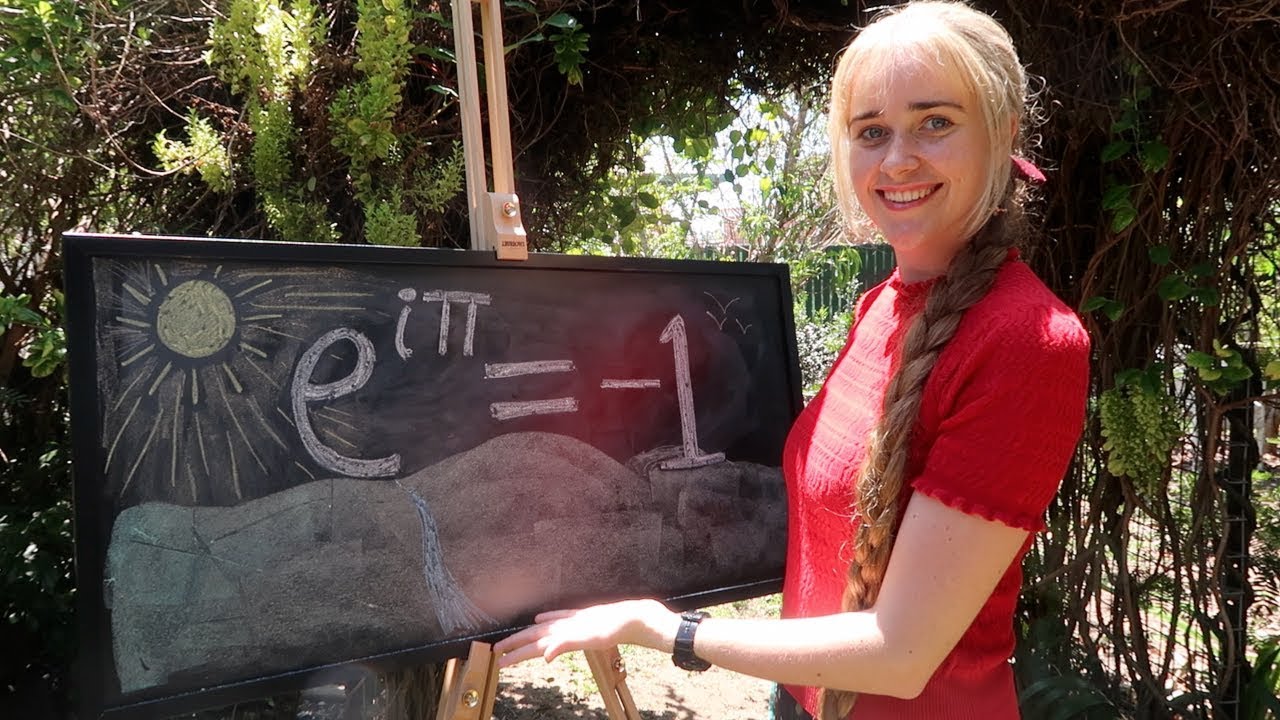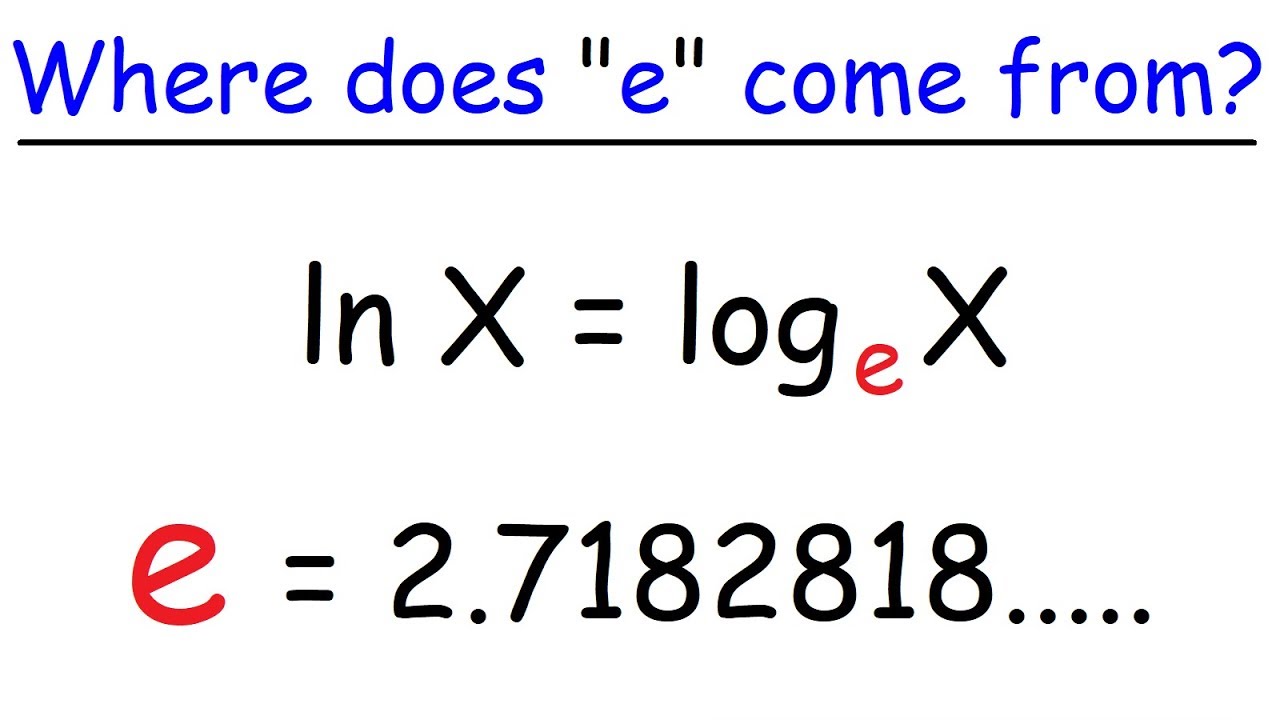e (Euler's Number) is seriously everywhere | The strange times it shows up and why it's so important
TLDRThis video explores the ubiquitous presence of Euler's number, e, in various real-world applications, starting with compound interest and extending to probability, calculus, and physics. It delves into how e emerges in scenarios like the secretary problem, infinite tetration, and the gamma function, highlighting its significance in signal analysis, quantum mechanics, and Euler's formula. The video also discusses the gamma function's role in higher dimensions and the surprising summation of even-dimensional unit spheres, concluding with the educational platform Brilliant.org, which hosts a variety of math and science courses.
Takeaways
- 📚 Euler's number (e) is approximately 2.71828 and has wide applications in mathematics and science, often showing up in real-world scenarios.
- 🏦 e is derived from the concept of compounding interest, representing the limit of (1 + 1/n)^n as n approaches infinity.
- 🎰 The number e appears in probability scenarios, such as the odds of losing a game with a one-in-a-million chance after playing it a million times.
- 🌂 e is relevant in calculating the probability that no one takes their own umbrella from a random stack after a party, which is about 1/e for a large number of guests.
- 🃏 In card shuffling, there's approximately a 1/e chance that no card remains in its original position after a random shuffle.
- 📝 The 'secretary problem' demonstrates the use of e in decision-making processes, suggesting an optimal strategy for selecting the best candidate from a series of interviews.
- 🔢 e is intrinsically linked to the concept of infinite tetration, where the function converges for values of x between 1/e and e.
- 📉 The exponential decay function, often involving e, is used to model phenomena such as cooling objects or damping oscillations.
- 📈 Euler's identity, e^(iπ) + 1 = 0, connects e with fundamental mathematical constants and is a cornerstone in various fields including physics and engineering.
- 🔢 The gamma function, which extends the factorial operation to non-integer values, includes e and is used in advanced areas of physics and mathematics.
- 🎓 Brilliant.org, the sponsor of the video, provides educational resources that delve into complex mathematical concepts like e and its applications.
Q & A
What is Euler's number (e) and how is it derived?
-Euler's number, denoted as 'e', is approximately 2.71828 and is derived as the limit of (1 + 1/n)^n as n approaches infinity, where n is a very large number. It is the base of the natural logarithm and has widespread applications in mathematics and science.
How is Euler's number related to compounding interest?
-Euler's number is related to compounding interest as it represents the amount of money you would have in a bank account after one year with 100% interest compounded an infinite number of times per year.
What is the significance of 1/e in probability when dealing with small chances of winning?
-In probability, 1/e is the odds of losing a game with a one-in-a-million chance of winning if played a million times. It represents the threshold where the chance of losing every single time approaches a significant probability.
How does Euler's number appear in the context of shuffling a deck of cards?
-When shuffling a deck of cards randomly, there is approximately a 1/e chance that no card remains in its original position, especially when the number of cards is large.
What is the optimal strategy for interviewing candidates for a job based on a single criterion?
-The optimal strategy is to first interview 1/e (approximately 37%) of the candidates to establish a benchmark, then choose the next candidate who is better than the best of the first group, ensuring a 1/e chance of picking the best candidate overall.
How does Euler's number relate to the product of cutting a stick into pieces?
-When a stick is cut into pieces, the maximum product of the lengths of the pieces occurs when the number of divisions is such that the length of each piece is closest to e.
What is the significance of e in the context of infinite tetration?
-Infinite tetration, a function of the form x^x^x^..., converges for values of x between 1/e and e, and diverges for most other values.
How does the average number of random numbers needed to sum to more than one relate to e?
-When picking random numbers between 0 and 1 and summing them until the total exceeds 1, the average number of numbers needed is e.
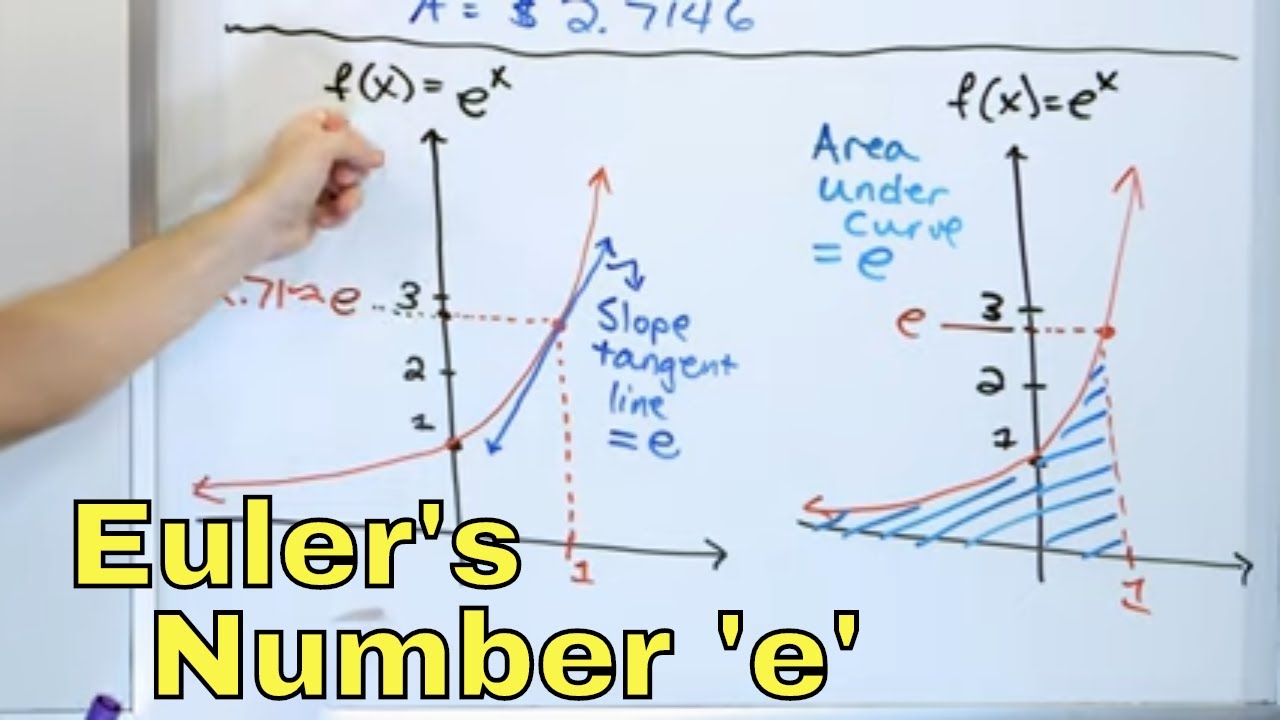
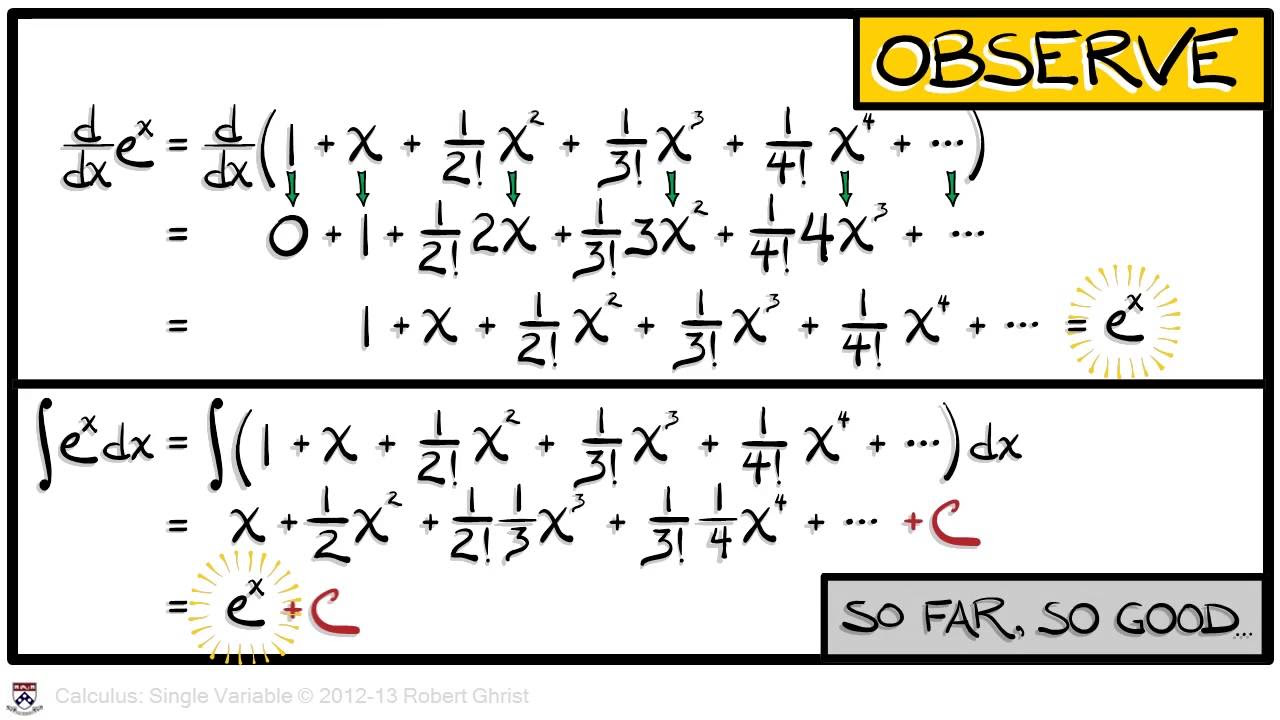
What is the unique property of the function e^x that relates to its rate of change?
-The function e^x has the unique property that its rate of change (derivative) is always the same as the function itself, meaning its velocity, acceleration, and so on, at any point are equal to the value of the function at that point.
How does Euler's formula demonstrate the relationship between exponential and sinusoidal functions?
-Euler's formula, e^(ix) = cos(x) + i*sin(x), shows that an exponential function with e as the base can be represented as a combination of sine and cosine functions, linking these mathematical concepts.
What is the connection between Euler's number and the gamma function?
-The gamma function is an extension of the factorial function that includes Euler's number in its definition. It allows for the calculation of factorials for non-integer values and is used in various advanced mathematical fields.
How does the summation of volumes of unit spheres in even dimensions relate to Euler's number?
-The sum of the volumes of unit spheres in every even dimension, from 0 to infinity, equals e to the power of pi, demonstrating a surprising connection between geometry and Euler's number.
Outlines
💡 Introduction to Euler's Number (e)
This video is sponsored by Brilliant and introduces Euler's number (e). It starts by recalling high school lessons on e and explains its mathematical definition and relevance through compounding interest. Various examples are used to show how e manifests in real-world scenarios, beginning with a practical explanation of compounding interest calculations and progressing to more abstract applications in probability.
📊 Probability and Random Events
The script discusses the appearance of e in probability theory and random events. Examples include calculating the odds of losing a lottery with a small winning chance, the likelihood of no one picking their own umbrella at a party, and shuffling a deck of cards. It also covers an optimal interview strategy using e and demonstrates how dividing a length into parts closest to e maximizes their product.
🔄 Infinite Tetration and Calculus
This section delves into the concept of infinite tetration, explaining the values for which the function converges. It references a university-level math problem demonstrating the average number of random numbers needed to exceed a sum of 1 is e. Additionally, the rate of change property of the exponential function e^x and its integral properties are highlighted, showing its ubiquity in mathematical and scientific contexts.
🔢 Euler's Formula and Its Applications
Euler's formula, which relates exponential functions to sinusoidal functions, is discussed. The script explains how this formula leads to the famous identity e^(iπ) + 1 = 0 and its application in signal analysis, quantum mechanics, and circuit analysis. The Fourier transform and its use in various fields such as audio processing and optics are mentioned, demonstrating the widespread utility of Euler's formula.
📈 Exponential Decay and Gamma Function
The video explores exponential decay equations and their applications, such as cooling objects and oscillating springs. It introduces the gamma function as an extension of the factorial function, showing how it calculates areas under specific curves and applies to higher-dimensional mathematics. Practical examples include quantum physics and astrophysics, highlighting the gamma function's relevance in advanced scientific calculations.
🔍 Further Real-World Applications and Conclusion
This part covers the appearance of e in calculating volumes of higher-dimensional spheres and normal distributions. It also discusses the Laplace transform in circuits and control systems. The video concludes by promoting Brilliant, an educational platform that offers math and science courses, encouraging viewers to explore complex algebra and other subjects to deepen their understanding of topics discussed in the video.
Mindmap
Keywords
💡Euler's number (e)
💡Compounding interest
💡Probability
💡Shuffling and probability
💡Secretary problem
💡Tetration
💡Euler's formula
💡Fourier transform
💡Gamma function
💡Exponential decay
💡Normal distribution
Highlights
Euler's number (e) is approximately 2.71828 and is derived from the limit of (1 + 1/n)^n as n approaches infinity.
E is frequently encountered in real-world applications, contrary to initial perceptions in high school.
The concept of compounding interest is used to intuitively explain the significance of e in mathematics.
e appears in various mathematical contexts, including probability, where it represents the odds of losing in games with small probabilities.
The probability of no one taking their own umbrella at a party, or a shuffled deck having no card in its original position, is approximately 1/e.
An optimal hiring strategy based on e is presented, maximizing the chance of selecting the best candidate from a pool of applicants.
The product of cutting a stick into pieces is maximized when the lengths are closest to e, demonstrating e's role in optimization problems.
Euler's number is central to infinite tetration, converging for values between 1/e and e.
The rate of change of e^x is always e^x, a unique property of the exponential function with e as the base.
Euler's formula, e^(ix) = cos(x) + i*sin(x), links exponential functions with sinusoidal functions and is instrumental in various scientific fields.
The gamma function extends the factorial operation to non-integer values and is related to e through its definition.
The volume of higher-dimensional spheres and their relation to e is discussed, showing e's ubiquity in advanced mathematical concepts.
E's applications extend to the normal distribution, Laplace transforms, and signal analysis, highlighting its pervasiveness in mathematical fields.
Brilliant.org is an educational platform that provides courses on complex algebra and the applications of e and Euler's formula.
The video concludes with an invitation to explore further applications of e and mathematical concepts through Brilliant's courses.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: