Review of all Derivative Rules | Calculus | jensenmath
TLDRThis video script offers a comprehensive review of derivative rules typically introduced in a high school calculus course. It walks through the constant multiple rule, power rule, product rule, quotient rule, and chain rule, demonstrating their application with various examples. The script also explains how to find the equation of a tangent line at a specific point on a curve using derivatives, reinforcing the concept of the derivative as the instantaneous rate of change. The examples are worked through step by step, ensuring clarity and understanding.
Takeaways
- 📚 The video is a review of derivative rules typically introduced in the first units of a high school calculus course.
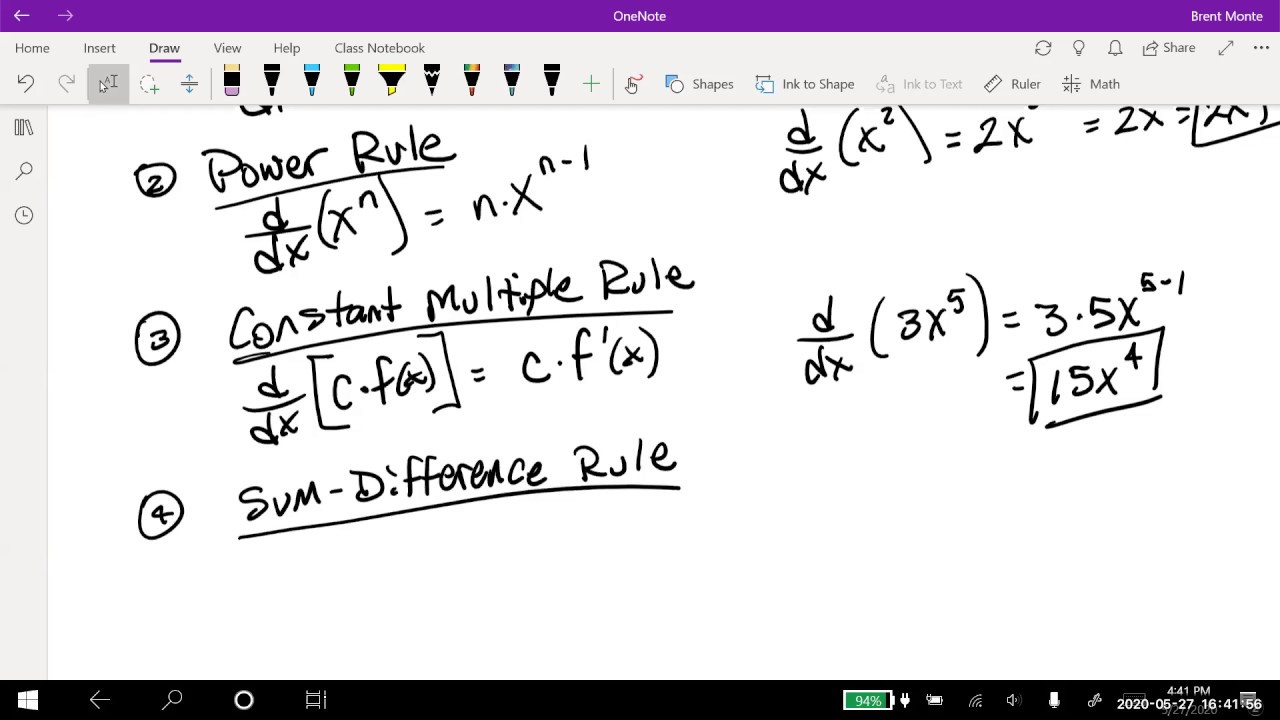
- 🔢 The script lists several fundamental derivative rules including the constant multiple rule, sum rule, product rule, quotient rule, power rule, and chain rule.
- 📝 Examples are provided to demonstrate the application of each derivative rule, starting with rewriting expressions in a form that makes differentiation straightforward.
- 👉 The power rule is explained with an example, showing how to differentiate terms with rational exponents and combine it with the constant multiple rule.
- ✂️ The product rule is illustrated by finding the derivative of a product of two functions, emphasizing the process of distribution and collection of like terms.
- 🔄 The quotient rule is demonstrated with an example, showing how to handle the derivative of a quotient by multiplying through by the denominator squared and simplifying.
- 🔗 The chain rule is applied to differentiate composite functions, focusing on the derivative of the outer function with respect to the inner function and then multiplying by the derivative of the inner function.
- 🔍 A combination of rules is used in more complex examples, such as when a product rule is applied within a chain rule, showing the need to factor and simplify the resulting expressions.
- 📈 The importance of understanding the meaning of derivatives is highlighted, explaining that they represent the instantaneous rate of change or the slope of the tangent line at a point on a curve.
- 📐 The process of finding the equation of a tangent line to a curve at a specific point is demonstrated, including evaluating the function and its derivative at that point to determine the slope of the tangent line.
- 📝 The final example ties together the concepts of derivatives by showing how to find the equation of a tangent line to a given curve at a specific x-value, emphasizing the practical application of derivative rules.
Q & A
What are the derivative rules mentioned in the video?
-The derivative rules mentioned are the constant multiple rule, sum rule, difference rule, product rule, quotient rule, power rule, and chain rule.
What is the first example function given in the video?
-The first example function is negative X to the 5 plus 5 X cubed plus the cube root of x squared.
How does the video suggest rewriting the cube root of x squared before differentiating?
-The video suggests rewriting the cube root of x squared as X to the power of 2/3.
What is the power rule for derivatives?
-The power rule for derivatives states that if you want to take the derivative of C times X to the N, it would equal C times N multiplied by X to the power of (N-1).
How is the product rule for derivatives explained in the video?
-The product rule for derivatives is explained as the derivative of a product of two functions f(x) and g(x), which equals the derivative of the first function times the second function plus the derivative of the second function times the first function.
What is the quotient rule for derivatives?
-The quotient rule for derivatives states that the derivative of a quotient of two functions equals the derivative of the top function times the bottom function minus the derivative of the bottom function times the top function, all over the bottom function squared.
How is the chain rule for derivatives described?
-The chain rule for derivatives is described as taking the derivative of the outside function with respect to the inside function and then multiplying by the derivative of the inside function.
What is the final simplified form of the first example function's derivative?
-The final simplified form of the first example function's derivative is negative 5 X to the 4 plus 15 x squared plus 2 over 3x to the 1/3.
What does the video use to explain the chain rule with a power of a function?
-The video uses the example function (3x - 2)^2 to explain the chain rule with a power of a function.
How does the video suggest finding the equation of the tangent line at a specific point?
-The video suggests finding the equation of the tangent line at a specific point by evaluating the original function at that point to get the coordinates and then using the derivative to find the slope at that point.
Outlines
📚 Derivative Rules Review
This paragraph introduces a review of derivative rules typically learned in a high school calculus course. The script lists the basic derivative rules such as the constant multiple rule, power rule, product rule, quotient rule, and chain rule, which are essential for differentiating functions. The speaker demonstrates the application of these rules through an example involving a function with multiple terms, including rewriting radicals as rational exponents and using the power and constant multiple rules to find the derivative of each term.
🔍 Applying the Product and Quotient Rules
This section delves into the application of the product and quotient rules for derivatives. The product rule is illustrated by finding the derivative of a product of two functions, showcasing the process of differentiating each function and combining the results. Similarly, the quotient rule is explained through an example, detailing the steps of differentiating the numerator and denominator and combining them according to the quotient rule formula. The paragraph emphasizes the importance of expanding and simplifying the expressions to find the final derivative.
🔗 Chain Rule and Factored Forms
The paragraph focuses on the chain rule and its combination with other derivative rules. It explains how to differentiate a function that is a power of another differentiable function, emphasizing the process of reducing the exponent by one and multiplying by the derivative of the base function. The speaker also discusses how to simplify expressions by factoring and expanding, particularly when dealing with complex derivatives that require the use of multiple rules, such as the chain and product rules together.
📈 Tangent Line Equations and Derivative Application
This paragraph reviews the concept of using derivatives to find the equations of tangent lines to a curve at a specific point. The speaker explains that the derivative of a function at a given point represents the slope of the tangent line at that point. The process involves evaluating the function and its derivative at the point of interest, then using these values to write the equation of the tangent line in point-slope form. The example provided walks through the calculation of the derivative of a complex function and the subsequent determination of the tangent line's equation at a particular x-value.
🧭 Final Review and Tangent Line Graphing
The final paragraph wraps up the review by summarizing the main derivative rules and their applications. It emphasizes the importance of understanding the meaning of derivatives as they relate to the instantaneous rate of change and the slope of the tangent line. The speaker provides a step-by-step guide on how to find the equation of a tangent line at a given x-value, including evaluating the function and its derivative at that point, and using these to form the tangent line equation. The paragraph concludes with a visual representation of the tangent line on a graph, illustrating its tangency to the function at the specified point.
Mindmap
Keywords
💡Derivative
💡Power Rule
💡Constant Multiple Rule
💡Product Rule
💡Quotient Rule
💡Chain Rule
💡Rational Exponent
💡Tangent Line
💡Instantaneous Rate of Change
💡Simplifying
Highlights
Introduction to derivative rules learned in a high school calculus course.
List of all derivative rules including constant multiple, sum, product, quotient, power, and chain rules.
Demonstration of using the power rule and constant multiple rule to differentiate a function.
Rewriting a radical expression as a power with a rational exponent for differentiation.
Differentiation of a function using the product rule for derivatives.
Explanation of the quotient rule for finding the derivative of a quotient of two functions.
Application of the chain rule to differentiate a power of a function that is itself differentiable.
Combining the chain rule and product rule to differentiate a complex function.
Use of common factoring to simplify the derivative of a complex expression.
Differentiation using quotient rule and chain rule in conjunction.
Simplification of derivatives by factoring and expanding terms.
Understanding the significance of derivatives as the slope of the tangent line at a point.
Finding the equation of a tangent line to a curve at a specific point using the derivative.
Evaluating the function and its derivative at a specific point to find the tangent line.
Simplification of the derivative expression for easier application to find the slope of the tangent line.
Final review of the main derivative rules covered in the video.
Encouragement to revisit individual topic videos for a more extensive review.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: