Confidence Intervals for Population Proportions

statslectures
15 Jul 201004:18
EducationalLearning
32 Likes 10 Comments

TLDRThis script explains the concept of confidence intervals for estimating population proportions. It uses a real-world example where 152 out of 200 households own at least one computer, calculating a sample proportion of 0.76. The video outlines the requirements for constructing a meaningful confidence interval, including sample size relative to the population and normal distribution approximation. It then demonstrates the calculation of a 95% confidence interval using the Z-score method, resulting in an estimated population proportion between 0.701 and 0.819.

Takeaways
  • 📊 Point estimates represent a single value of a statistic that estimates a parameter, such as a population proportion.
  • 🔍 To estimate the population proportion more accurately, a confidence interval is constructed around the sample proportion.
  • 🏷️ The sample proportion is calculated by dividing the number of successful outcomes (x) by the sample size (n).
  • 🌐 A confidence interval provides a range of values that is likely to contain the true population proportion.
  • 📉 Two conditions must be met for constructing a meaningful confidence interval: the sample size should not be more than 5% of the population size, and a certain equation must be satisfied to ensure the sample is approximately normally distributed.
  • 🔢 The equation to check for normal distribution involves the sample size and the sample proportion, and if it's greater than 10, it indicates normal distribution.
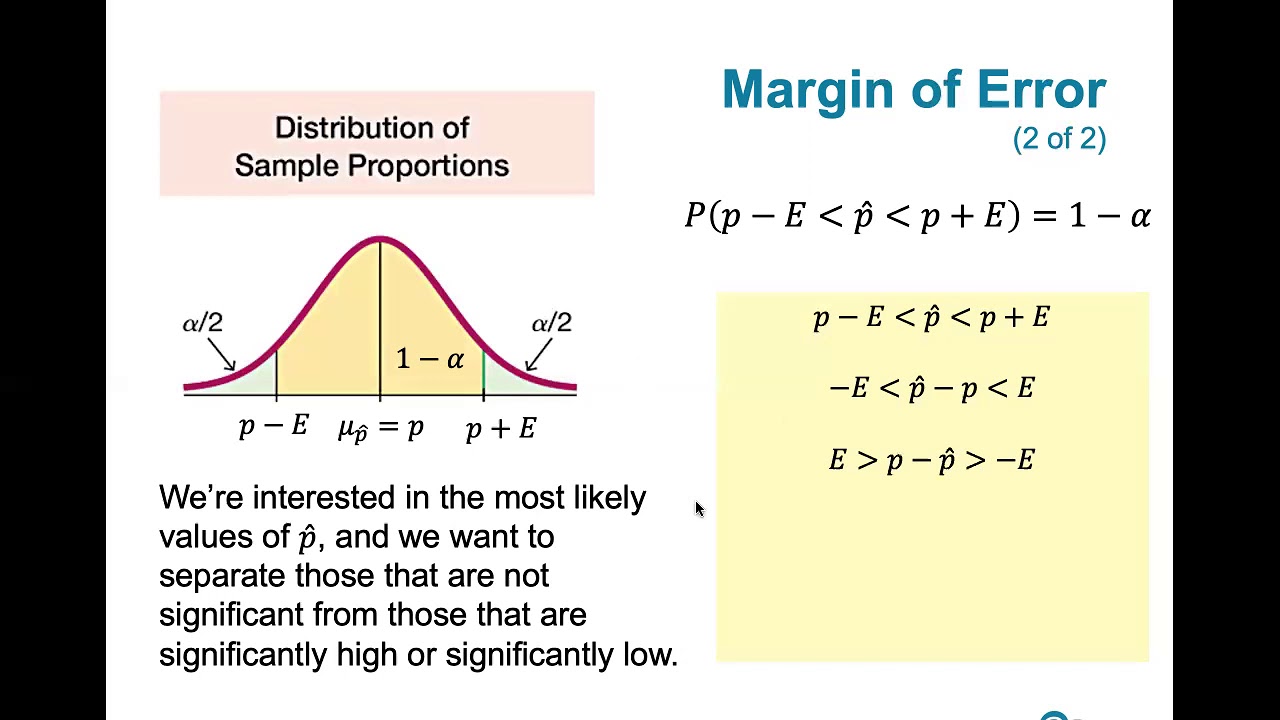
  • 📚 A 95% confidence interval is sought, which means that 95% of the area under the normal distribution curve is within the interval, with 2.5% in each tail.
  • 📉 The Z-score for a 95% confidence interval with 2.5% in each tail is 1.96, which is found using a Z-table.
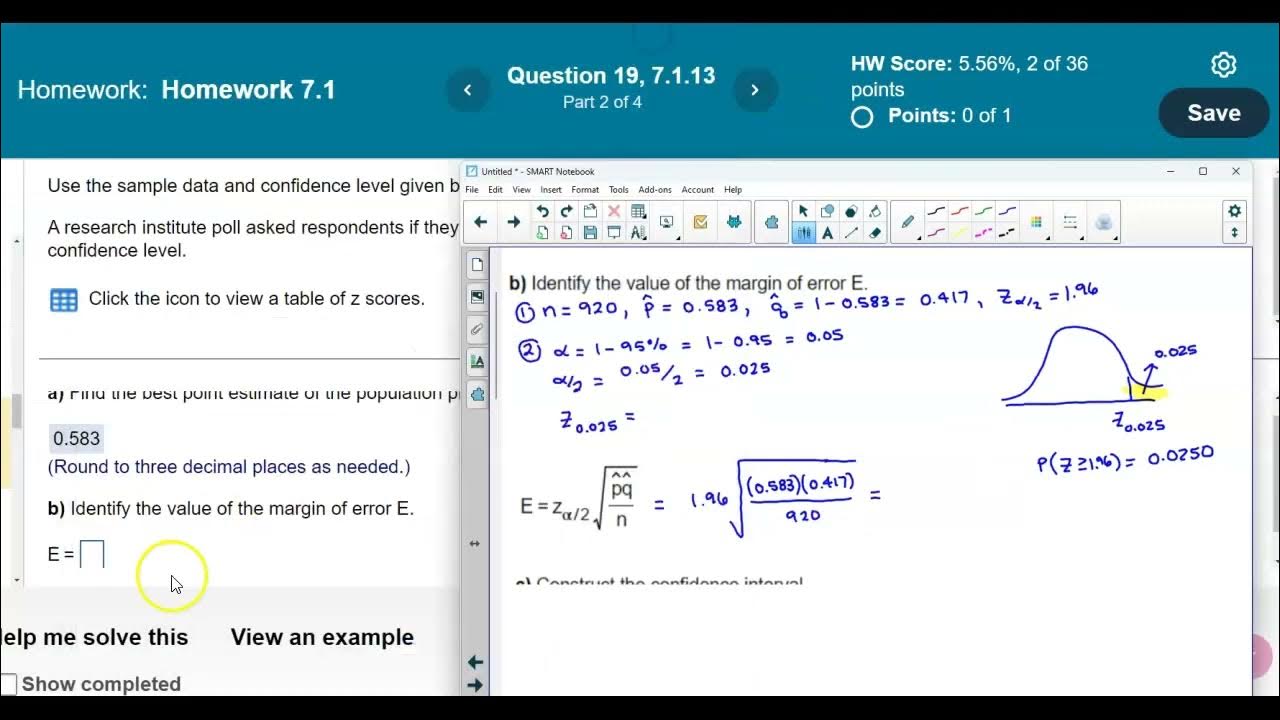
  • ➕ The margin of error is calculated by multiplying the Z-score by the standard error of the sample proportion, which is the square root of (p * (1 - p) / n).
  • 📝 The final confidence interval is the point estimate (sample proportion) plus or minus the margin of error.
  • 🏠 In the example provided, the 95% confidence interval for the proportion of households with at least one computer is between 70.1% and 81.9%.
Q & A

  • What is a point estimate in statistics?

    -A point estimate is a single value of a statistic that is used to estimate the value of a parameter.

  • What is the purpose of creating a confidence interval around a point estimate?

    -The purpose of creating a confidence interval is to provide a range of values that are likely to contain the true population parameter, giving a more realistic impression of what the actual value may be.

  • What is the sample proportion in the given example?

    -The sample proportion in the example is calculated by dividing the number of households with at least one computer (152) by the total number of households surveyed (200), which equals 0.76 or 76%.

  • What are the two requirements for constructing a meaningful confidence interval about the population proportion?

    -The two requirements are: 1) The sample size must be no more than 5% of the population size, and 2) The sample must meet the condition that the quantity (n * p * (1 - p)) is greater than 10, indicating an approximately normal distribution.

  • Why is it necessary to check if the sample size is no more than 5% of the population size?

    -This requirement ensures that the sample is not too large relative to the population, which helps maintain the validity of the confidence interval for the population proportion.

  • What does it mean if the condition (n * p * (1 - p)) is greater than 10?

    -If this condition is met, it indicates that the sample proportion has an approximately normal distribution, which allows for the use of the Z-distribution in calculating the confidence interval.

  • What is the significance of the Z score in constructing a confidence interval?

    -The Z score represents the number of standard deviations from the mean that corresponds to the tail area of the normal distribution. It is used to determine the margin of error in the confidence interval.

  • What is the Z score used for a 95% confidence interval?

    -For a 95% confidence interval, the Z score used is 1.96, which corresponds to the point where 2.5% of the data is in each tail of the normal distribution, leaving 95% in the middle.

  • How is the margin of error calculated in the context of a confidence interval for a population proportion?

    -The margin of error is calculated as the Z score multiplied by the standard error of the proportion, which is the square root of ((p * (1 - p)) / n).

  • What is the confidence interval for the proportion of households with at least one computer in the given example?

    -The 95% confidence interval for the proportion of households with at least one computer is between 70.1% and 81.9%.

  • What does it mean to be 95% confident of a value?

    -Being 95% confident of a value means that if we were to repeat the sampling process many times, we expect that 95% of the resulting confidence intervals would contain the true population parameter.

Outlines
00:00
📊 Understanding Point Estimates and Confidence Intervals

This paragraph introduces the concept of point estimates and confidence intervals in statistics. A point estimate is a single value that serves as the best guess for a population parameter, such as the proportion of households with at least one computer. The paragraph explains the need to create a confidence interval around this point estimate to provide a range that is likely to contain the true population proportion. An example is given where a sample of 200 households is used to estimate the proportion of households with at least one computer, with the sample proportion calculated as 76%. The importance of meeting two requirements for constructing a meaningful confidence interval is also highlighted: the sample size must be less than 5% of the population size, and a condition related to the distribution of the sample proportion must be met to ensure it is approximately normal.

Mindmap
Keywords
💡Point estimate
A point estimate is a single value of a statistic that serves as the best guess for the parameter it is estimating. In the context of the video, the point estimate is used to represent the sample proportion, which is calculated as the number of households with at least one computer (152) divided by the total number of households surveyed (200), resulting in a point estimate of 0.76 or 76%.
💡Confidence interval
A confidence interval is a range of values, derived from a data sample, that is likely to contain the value of an unknown population parameter. The video script discusses creating a confidence interval around the point estimate of the sample proportion to estimate the population proportion. The script provides an example of constructing a 95% confidence interval for the proportion of households with at least one computer.
💡Population proportion
The population proportion refers to the ratio of a particular characteristic within an entire population. In the video, the population proportion is the actual, unknown ratio of households that have at least one computer. The script aims to estimate this value through the creation of a confidence interval based on the sample data.
💡Sample proportion
The sample proportion is the ratio of the number of successes (in this case, households with at least one computer) to the total number of observations in the sample. The script calculates the sample proportion as 152 out of 200 households, which is 0.76, to represent the proportion in the sample that possesses the characteristic of interest.
💡Margin of error
The margin of error is the range plus or minus a certain value from the point estimate, indicating the amount of error that is expected in the estimate. In the video, the margin of error is calculated as part of the confidence interval formula to determine the range within which the true population proportion is likely to fall.
💡Normal distribution
A normal distribution is a continuous probability distribution in which values are symmetrically distributed around the mean. The script mentions that if the sample size meets certain criteria, the sampling distribution of the sample proportion is approximately normally distributed, allowing for the use of Z-scores in constructing the confidence interval.
💡Z-score
A Z-score represents the number of standard deviations a data point is from the mean of a normal distribution. The video script uses Z-scores from the standard normal distribution table to determine the critical value needed for calculating the margin of error in the 95% confidence interval.
💡Z table
A Z table is a statistical tool used to find the Z-scores associated with given probabilities. In the script, the Z table is used to find the Z-score of 1.96, which corresponds to the critical value for a 95% confidence interval with 2.5% in each tail.
💡Alpha
Alpha (α) is the probability of making a Type I error, or the likelihood of rejecting a true null hypothesis. In the context of the video, alpha is the total probability in the tails of the distribution outside the confidence interval. The script mentions α/2, which is the probability allocated to each tail, resulting in 0.025 for a 95% confidence interval.
💡Type I error
A Type I error occurs when a true null hypothesis is incorrectly rejected. While the video script does not delve deeply into Type I errors, it mentions alpha as the probability of making such an error, which is related to the confidence level chosen for the interval.
💡Lower bound and upper bound
The lower and upper bounds are the limits of the confidence interval, representing the range within which the population parameter is estimated to lie. The script calculates these bounds using the sample proportion, the Z-score, and the margin of error, concluding that the proportion of households with at least one computer is estimated to be between 70.1% and 81.9% with 95% confidence.
Highlights

Point estimates are single values that estimate the value of a parameter.

A confidence interval is created around a point estimate to estimate the population proportion.

The sample proportion is calculated as the number of successes divided by the sample size.

A single sample may not accurately represent the entire population.

Confidence intervals provide a more realistic impression of the actual population proportion.

Two requirements for constructing a meaningful confidence interval about the population proportion are discussed.

The sample size should be no more than 5% of the population size.

The sample should have an approximately normal distribution to be compared to the normal Z-distribution.

A 95% confidence interval is constructed to estimate the population proportion.

The sample meets the requirement of being less than 5% of the population size.

The sample's distribution is approximately normal, allowing for comparison to the normal distribution.

The margin of error is calculated using the Z-score for a 95% confidence interval.

The Z-score of 1.96 is used for a 95% confidence interval with 2.5% in each tail.

The confidence interval is calculated as the point estimate plus or minus the margin of error.

The lower and upper bounds of the confidence interval are determined.

The 95% confidence interval for the proportion of households with at least one computer is between 70.1% and 81.9%.

The process of constructing a confidence interval around a population proportion is demonstrated.

Transcripts

Browse More Related Video

Confidence Interval for a population proportion | Solved Problems

7.1.4 Estimating a Population Proportion - Margin of Error and Computing Confidence Intervals

Confidence interval example | Inferential statistics | Probability and Statistics | Khan Academy

Math 14 7.1.13 Find the point estimate, margin of error & confidence interval of pop. proportion p.

Elementary Stats Lesson #15

How to construct a confidence interval for the proportion, an example

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Confidence IntervalPopulation ProportionStatistical AnalysisSample SizeNormal DistributionZ-ScoreEstimation MethodHousehold SurveyData InterpretationStatistical Tools