Calculus AB Homework 7.4 Disk and Washer Method
TLDRThis video tutorial guides viewers through solving various calculus problems involving volumes of solids of revolution. It covers the disk and washer methods, with step-by-step instructions on setting up integrals and evaluating them to find volumes. The script includes examples such as revolving regions bounded by functions like y=x^(5/7), y=x^3, and y=x^2 around different axes, as well as more complex scenarios involving intersections and horizontal rotations. The video is designed to help students master these integral calculus concepts with clear explanations and visual aids.
Takeaways
- 📐 The video covers solving unit 7 homework problems 31 through 41.
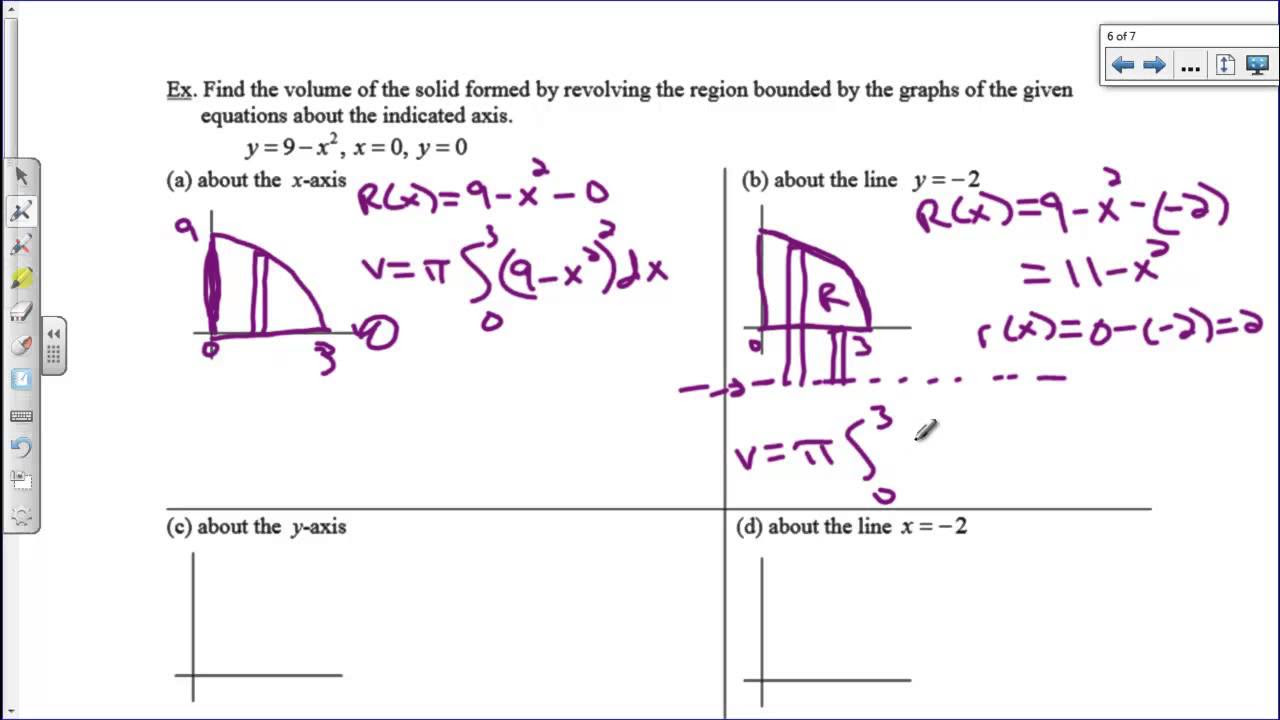
- 📊 Problem 31 involves finding the volume of a solid of revolution by rotating the region bounded by the x-axis and the graph of y = fifth root of x from x = 0 to x = 1 about the x-axis, using the disk method.
- 📝 For problem 32, the task is to find the volume of the solid of revolution formed by rotating the region bounded by the x-axis and the graph of y = x^3 from x = 1 to x = 2 about the x-axis, also using the disk method.
- 🔍 Problem 33 requires finding the volume of the solid of revolution formed by rotating the region bounded by the x-axis and the graph of y = x^2 * sqrt(2 - cos(x)^5) from x = 0 to x = 2 about the x-axis.
- 🔄 In problem 34, the focus is on finding the volume of the solid of revolution by rotating the region bounded by the x-axis and the graph of x = y^3 from y = 0 to y = 1 about the y-axis, using the dy method.
- 📏 Problem 35 involves finding the volume of the solid of revolution formed by rotating the region bounded by the y-axis and the graph of y = seventh root of x^5 from y = 0 to y = 1 about the y-axis, using the dy method.
- 📈 For problem 36, the task is to find the area of the region bounded by the graphs of y = ln(x) and y = x - 2.
- 🌀 Problem 37 extends problem 36 to find the volume of the solid generated when the region is rotated about the horizontal line y = -3, using the washer method.
- ⚖️ In problem 38, the challenge is to find the volume of the solid generated when the region from problem 36 is rotated about the y-axis.
- 📉 Problem 39 involves finding the volume of the solid resulting from rotating the region enclosed by y = x^2 and y = x^3 about the vertical line x = 1.
Q & A
What is the solid of revolution formed by rotating the region bounded by the x-axis and the graph of y equals the fifth root of x from x equals zero to x equals one?
-The solid of revolution is a 3D shape created by spinning the given 2D region around the x-axis. In this case, the region is bounded by the x-axis and the curve y = x^(1/5) from x = 0 to x = 1.
What method is used to find the volume of the solid formed by rotating the region around the x-axis in problem 31?
-The Disk Method is used, which involves integrating the area of infinitesimally thin disks perpendicular to the axis of rotation over the given interval.
What is the integral set up for finding the volume of the solid in problem 31?
-The integral set up is π times the integral from 0 to 1 of (x^(1/5))^2 dx, which simplifies to π times the integral from 0 to 1 of x^(2/5) dx.
How is the volume of the solid in problem 31 calculated?
-The volume is calculated by evaluating the integral from 0 to 1 of x^(2/5), then multiplying by π and the difference of the evaluated limits, resulting in (5π/7) as the final answer.
What is the region bounded by the x-axis and the graph of y equals x cubed from x equals 1 to x equals two?
-The region is a portion of the curve y = x^3 between x = 1 and x = 2, which is then rotated around the x-axis to form a solid of revolution.
What is the method used to find the volume of the solid formed by rotating the region bounded by y equals x cubed from x equals 1 to x equals two around the x-axis?
-The method used is the same as in problem 31, which is the Disk Method, integrating the square of the radius (x^3) over the interval from 1 to 2.
What is the integral for finding the volume of the solid in problem 32?
-The integral is π times the integral from 1 to 2 of x^3 dx, which simplifies to π times the integral of x^6/6 dx from 1 to 2.
What is the volume of the solid formed by rotating the region bounded by y equals x squared times the square root of 2 minus cosine x to the fifth from x equals 0 to x equals 2 about the x-axis?
-The volume is found using a more complex integral involving a substitution method and is approximately 39.86 cubic units.
How is the volume of the solid in problem 33 calculated?
-The volume is calculated by integrating the squared difference of the functions (x^2 * (sqrt(2) - cos(x))^5) over the interval from 0 to 2, then multiplying by π.
What is the washer method used for?
-The washer method is used to find the volume of a solid of revolution when the region is rotated around an axis that is not the natural boundary of the region, creating an annular shape with an inner and outer radius.
What is the integral for finding the volume of the solid in problem 34 when rotated about the y-axis?
-The integral is π times the integral from 0 to 1 of (y^(7/5))^2 dy, which simplifies to π times the integral from 0 to 1 of y^(14/5) dy.
What is the volume of the solid resulting from rotating the region enclosed by y equals the seventh root of x to the fifth from y equals zero to y equals one about the y-axis?
-The volume is π times the integral from 0 to 1 of y^(14/5) dy, resulting in a volume of (5π/19).
What is the process for finding the volume of the solid formed by rotating the region bounded by y equals ln(x) and y equals x minus 2 about the horizontal line y equals negative three?
-The process involves finding the points of intersection, setting up the washer method with an outer and inner radius, and integrating the squared difference of the radii over the interval from the points of intersection.
What is the volume of the solid formed by rotating the region bounded by y equals ln(x) and y equals x minus 2 about the y-axis?
-The volume is found by using the washer method with the equations solved for x in terms of y, integrating the squared difference of the outer and inner radii over the interval from negative 1.8414 to 1.1462, resulting in a volume of approximately 5.4 cubic units.
What is the volume of the solid resulting from rotating the region enclosed by y equals x squared and y equals x cubed about the vertical line x equals 1?
-The volume is π times the integral from 0 to 1 of (1 - sqrt(y))^2 - (1 - cbrt(y))^2 dy, resulting in a volume of approximately 0.209 cubic units.
What is the volume of the solid resulting from rotating the region enclosed by y equals x squared and y equals x cubed about the vertical line x equals negative one?
-The volume is π times the integral from 0 to 1 of (cbrt(y) + 1)^2 - (sqrt(y) + 1)^2 dy, resulting in a volume of approximately 0.838 cubic units.
What is the volume of the solid resulting from rotating the region enclosed by y equals cos(x) and y equals x squared about the horizontal line y equals negative one?
-The volume is π times the integral from 0 to 0.8767 of (sin(x) + 1)^2 - (x^2 + 1)^2 dx, resulting in a volume of approximately 1.132 cubic units.
Outlines
📚 Calculus Homework: Solid of Revolution
This paragraph introduces a calculus homework problem set focused on finding volumes of solids formed by revolving regions around the x-axis. The specific problem involves the function y = (fifth root of x) from x = 0 to x = 1, and the solution uses the disk method to set up an integral with respect to x. The process includes sketching the graph, identifying the region of integration, and calculating the volume by integrating the square of the function's height over the given interval, resulting in a final answer of five PI over seven.
📐 Rotating Regions to Form Solids: Volume Calculation
The second paragraph continues the theme of calculating volumes of solids of revolution, this time revolving around the x-axis the region bounded by y = x cubed from x = 1 to x = 2. The method involves setting up an integral for the volume, pi times the radius squared, with the radius being the function's value minus zero. The integral is evaluated using the power rule, leading to a final volume of 127 over 7 times pi, which is approximately 33.3 found.
🔍 Advanced Solid of Revolution: Complex Function Integration
This paragraph presents a more complex problem of finding the volume of a solid formed by revolving the region bounded by y = x squared times the square root of 2 minus cosine x to the fifth, from x = 0 to x = 2, around the x-axis. The solution involves a detailed setup using the disk method, with the radius being the function's value squared. The integral is complex and requires substitution to solve, leading to a final volume of approximately 39.86 cubic units.
📉 Volume of Solids Generated by Rotating Specific Functions
The fourth paragraph discusses the calculation of volumes of solids formed by revolving regions around the y-axis for two different functions: x = y cubed and y = (seventh root of x) to the fifth. Both problems are approached using horizontal rectangles (dy problems) and involve setting up integrals for the volume, which are then evaluated using the power rule. The results are pi over seven and 5 pi over 19, respectively.
📈 Intersection Points and Solid of Revolution Around a Line
The focus of this paragraph is on finding the intersection points of two graphs, y = ln(x) and y = x - 2, and calculating the area of the region they enclose. The points of intersection are determined using a calculator, and the area is found by integrating the difference between the two functions from the points of intersection. Additionally, the paragraph explores the volume of the solid formed when this region is rotated around the horizontal line y = -3, using the washer method to find the volume.
📊 Volume Calculation with Rotating Regions Around Multiple Axes
This paragraph involves calculating the volume of solids formed by revolving a region enclosed by two functions, f(x) = 1/4 + sine(πx) and g(x) = 4 to the power of -x, around different axes. The process includes finding the points of intersection of the functions, calculating the area bounded by the functions and the x-axis, and then finding the volume when the region is revolved around a horizontal line y = 8 and around the y-axis. The washer method is used for revolving around the horizontal line, and the disk method for revolving around the y-axis.
🔄 Rotating Complex Regions: Washer and Disk Methods
The paragraph discusses the process of finding the volume of solids formed by revolving complex regions around a vertical line and a horizontal line, using both the washer and disk methods. The regions are enclosed by y = x squared and y = x cubed, and the axis of rotation is x = 1 for the washer method and x = -1 for the disk method. The calculations involve setting up integrals for the outer and inner radii and evaluating them to find the volume of the resulting solids.
📐 Solid of Revolution Around Horizontal and Vertical Lines
The final paragraph presents the calculation of volumes of solids formed by revolving the region enclosed by y = x squared and y = x cubed around the vertical line x = -1 and the horizontal line y = -1. The washer method is used for the vertical rotation, involving the calculation of outer and inner radius squares, while the disk method is used for the horizontal rotation, with a similar approach. The integrals are evaluated to find the volumes, which are 0.838 and 1.132, respectively.
Mindmap
Keywords
💡Solid of Revolution
💡Disk Method
💡Integral
💡Riemann Sum
💡Power Rule
💡Graph of a Function
💡Volume Calculation
💡Washer Method
💡Points of Intersection
💡u-Substitution
Highlights
Introduction to solving unit 7 homework problems 31 through 41 involving volume calculations of solids of revolution.
Explanation of using the disk method to find the volume of a solid formed by rotating the region bounded by y = x^(1/5) from x = 0 to x = 1 around the x-axis.
Demonstration of setting up the integral for the volume calculation with respect to x, integrating from 0 to 1.
Calculation of the volume of a solid formed by rotating the region bounded by y = x^3 from x = 1 to x = 2 around the x-axis using the power rule.
Application of u-substitution in the integral to find the volume of a solid formed by rotating the region bounded by y = x^2 * (√2 - cos(x))^5 from x = 0 to x = 2 around the x-axis.
Use of the washer method to calculate the volume of a solid formed by rotating the region bounded by x = y^3 from y = 0 to y = 1 around the y-axis.
Finding the volume of a solid formed by rotating the region bounded by y = (x^(5/7))^7 from y = 0 to y = 1 around the y-axis using horizontal rectangles.
Solving for the intersection points of y = ln(x) and y = x - 2 to find the area of the region R and its subsequent volume when rotated about y = -3.
Utilization of the washer method to calculate the volume of a solid generated by rotating the region R about the y-axis.
Identification of intersection points for the functions f(x) = 1/4 + sin(πx) and g(x) = 4^(-x) and calculation of the area bounded by them.
Calculation of the volume of the solid generated when the region enclosed by f(x) and g(x) is revolved about the horizontal line y = 8.
Finding the volume of the solid resulting from rotating the region enclosed by y = x^2 and y = x^3 about the vertical line x = 1 using the washer method.
Solving the volume of the solid resulting from rotating the region enclosed by y = x^2 and y = x^3 about the vertical line x = -1.
Calculation of the volume of the solid resulting from rotating the region enclosed by y = cos(x) and y = x^2 about the horizontal line y = -1.
Final problem overview: finding the volume of the solid resulting from rotating the region enclosed by y = x^2 and y = x^3 about the vertical line x = -1.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: