Calculus AB Homework 5.4: Speed and Distance Traveled

Michelle Krummel

5 Feb 201838:43

EducationalLearning

32 Likes 10 Comments

TLDRIn this video, we work through particle motion problems, specifically focusing on determining whether the speed of a particle is increasing or decreasing at a given time, analyzing intervals of movement direction, and calculating average velocity. We explore the position, velocity, and acceleration functions, use factoring techniques, and interpret graphs to find critical points and changes in direction. The video includes step-by-step explanations and calculations, aiming to clarify complex concepts in particle motion.

Takeaways

📚 The video covers Unit 5 homework problems 25 to 28, which involve particle motion.
🔍 Problem 25 asks whether the speed of a particle is increasing or decreasing at a specific time, using the given position function and its derivatives for velocity and acceleration.
📉 The velocity function is derived by differentiating the position function, and its sign at time T=2.5 is used to determine if the speed is increasing or decreasing.
🔺 The acceleration function is the derivative of the velocity function, and its sign indicates whether the particle is speeding up or slowing down.
📈 Problem 26 involves a velocity graph, and the intervals where the particle moves to the right are identified by where the graph is above the x-axis.
⏹️ The particle is momentarily stopped and changing direction when its velocity is zero and there's a sign change in velocity.
📊 Problem 27 requires calculating the average velocity over a given time interval using the position function and the change in position over time.
🚫 The particle is moving to the left when the velocity, derived from the position function, is negative.
🔍 Problem 28 involves finding the velocity and acceleration at a specific time and using them to describe the particle's motion at that instant.
📏 The maximum velocity on a given interval is found by analyzing the velocity function's behavior, including its critical points and end-point values.
📏 The total distance moved by a particle on an interval is calculated by considering the intervals where the particle changes direction and summing the absolute values of the displacements.
🔄 When acceleration is zero, the particle's velocity is determined by evaluating the velocity function at the time when the acceleration function equals zero.

Q & A

What is the given position function for the particle in problem 25?
-The position function is X(t) = t^3 - 9t^2 + 24t.
How do you find the velocity function from the position function?
-The velocity function V(t) is the derivative of the position function X(t). For X(t) = t^3 - 9t^2 + 24t, V(t) = 3t^2 - 18t + 24.
Is the particle's speed increasing or decreasing at t = 2.5?
-To determine if the speed is increasing or decreasing, you need to check the signs of velocity and acceleration at t = 2.5. Since both V(2.5) and A(2.5) are negative, the speed of the particle is increasing at t = 2.5.
How is the acceleration function derived from the velocity function?
-The acceleration function A(t) is the derivative of the velocity function V(t). For V(t) = 3t^2 - 18t + 24, A(t) = 6t - 18.
What is the particle's acceleration at t = 2.5?
-The acceleration A(2.5) is calculated as 6(2.5) - 18 = -3, so the acceleration at t = 2.5 is negative.
On what intervals is the particle moving to the right according to the velocity graph?
-The particle is moving to the right where the velocity is positive, which is from t = 0 to t = 1 and t = 5.25 to t = 7.
On what intervals is the particle moving to the left?
-The particle is moving to the left where the velocity is negative, which is from t = 1 to t = 5.25.
When is the particle momentarily stopped and changing direction?
-The particle is momentarily stopped and changing direction at t = 1 and t = 5.25, where the velocity changes sign.
What is the acceleration of the particle between t = 2 and t = 3, and t = 7 and t = 9?
-The acceleration is zero between t = 2 and t = 3, and t = 7 and t = 9, since the derivative of the velocity is zero in these intervals.
How do you find the average velocity of the particle on the interval t = 1 to t = 2?
-The average velocity is calculated as the change in position divided by the change in time, which is (P(2) - P(1)) / (2 - 1).

Outlines

00:00

📚 Particle Motion Analysis

The video begins with an exploration of unit 5 homework problems 25 to 28, focusing on particle motion. The position function of a particle is given by X(T) = T^3 - 9T^2 + 24T for T > 0. The goal is to determine if the speed is increasing or decreasing at T = 2.5. This involves calculating the velocity V(T) = 3T^2 - 18T + 24 and its derivative, the acceleration, a(T) = 6T - 3. By evaluating these at T = 2.5, it's concluded that the particle is speeding up at this time, as both velocity and acceleration share the same sign and are positive.

05:00

📈 Velocity Graph Interpretation

The script moves on to problem 26, which involves interpreting a velocity graph of a particle over time. The intervals during which the particle moves to the right (where velocity is positive) are identified as 0 to 1 and approximately 5.2 to 7 seconds. The particle is slowing down on intervals where the velocity graph is decreasing, which is from 0 to 1, 3 to 5.25, and 6 to 7 seconds. The explanation involves taking the absolute value of the velocity graph to determine slowing down intervals and also considers the direction of velocity changes.

10:04

🛑 Particle Momentary Stop and Direction Change

In problem 27, the focus is on identifying when the particle is momentarily stopped and changing direction. This occurs when the velocity is zero and the sign of the velocity changes. The times identified for momentary stops are T = 1 and T = 5.25, with direction changes occurring at these times as well. Additionally, the script discusses when the acceleration is zero, which is between T = 2 and T = 3, and between T = 7 and T = 9, excluding the endpoints.

15:06

🚀 Particle Motion with Given Position Function

The fourth paragraph addresses a scenario where a particle's position function is given by P(T) = T^3 - 4T^2 - 3T + 1 for T ≥ 0. The task is to find the average velocity over the interval from T = 1 to T = 2 and to determine when the particle is moving to the left, which is when the velocity is negative. The x-intercepts of the velocity function are calculated to be at T = -1/3 and T = 3, indicating the intervals of leftward motion.

20:07

🔍 Detailed Analysis of Particle Motion at Specific Time

Paragraph 5 delves deeper into the motion of the particle at T = 3 seconds by examining the first and second derivatives of the position function, P'(T) and P''(T). It is found that P'(3) = 0, indicating the particle is momentarily at rest, and P''(3) = 10, suggesting positive acceleration. This implies the particle is about to change direction from moving left to right.

25:08

📉 Maximum Velocity and Total Distance Calculation

The script then tackles the problem of finding the maximum velocity on the interval from T = 0 to T = 3 seconds. It is determined that the maximum velocity occurs at T = 3 seconds, with a value of zero. Additionally, the total distance moved by the particle on the interval from T = 1 to T = 5 seconds is calculated by considering changes in direction at T = 3 seconds, resulting in a total distance of 40 feet.

30:14

🔧 Particle Motion with Variable Time Function

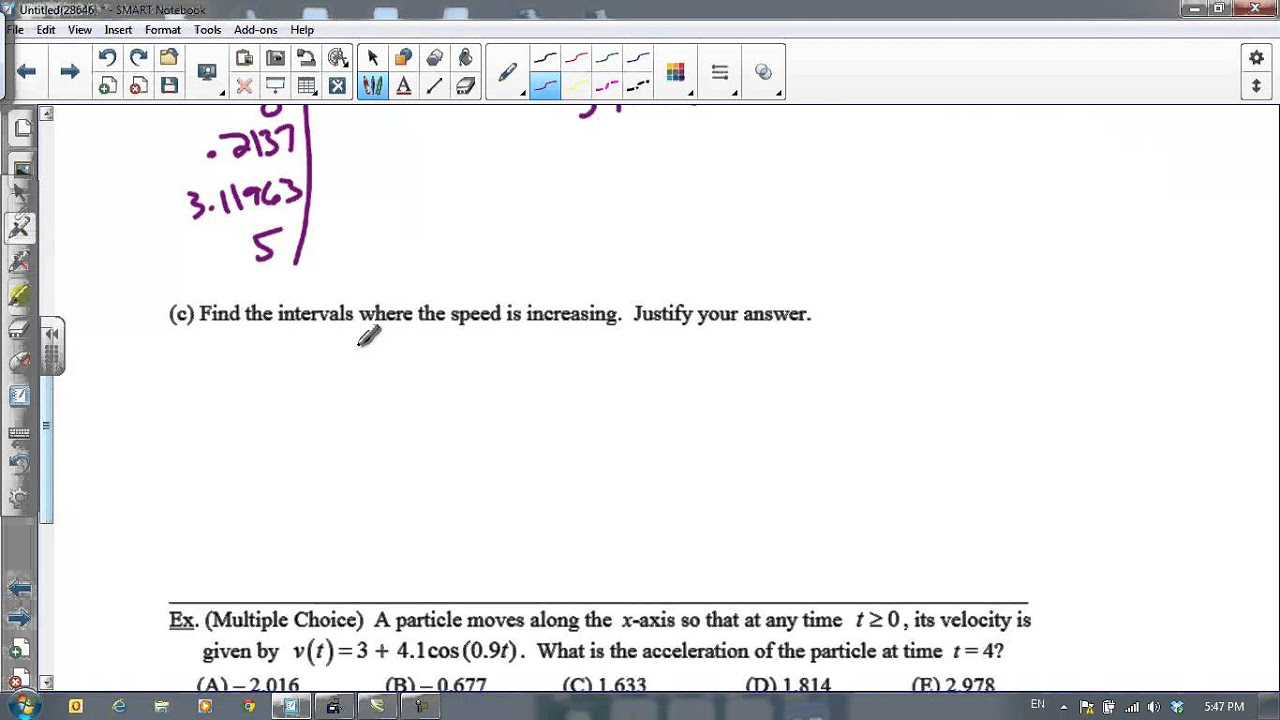
The final paragraph introduces a new position function, s(T), defined for T between 0 and π. The challenge is to find the velocity of the particle when its acceleration is zero. By setting the acceleration equation to zero and solving for T, a time of approximately 1.318 is found. The velocity at this specific time is then calculated to be 2.555 when rounded to three decimal places.

Mindmap

Keywords

💡Particle Motion

Particle motion refers to the movement of a particle along a path, often in a physics context. In the video, this concept is central as the instructor analyzes the position, velocity, and acceleration of a particle over time. The script discusses how the particle's speed changes at specific times, such as when T equals 2.5, by examining the velocity and acceleration functions.

💡Position Function

A position function in physics represents the location of an object as a function of time. In the script, the position function is given by X(T) = T^3 - 9T^2 + 24T, which describes the particle's position along a path in relation to time T. This function is fundamental to determining other quantities like velocity and acceleration.

💡Velocity

Velocity is a vector quantity that describes the rate of change of an object's position with respect to time. The script defines the velocity function V(T) as the derivative of the position function, which is used to analyze whether the particle's speed is increasing or decreasing at time T equals 2.5.

💡Acceleration

Acceleration is the rate of change of velocity with respect to time, indicating how quickly the velocity of an object is changing. In the script, the acceleration function is derived from the velocity function and is used to determine the particle's behavior, such as speeding up or slowing down, at a specific time T equals 2.5.

💡Derivative

In calculus, a derivative represents the rate at which a function changes with respect to its variable. The script uses derivatives to find the velocity (first derivative of position) and acceleration (second derivative of position) of the particle, which are essential for analyzing motion.

💡Factoring

Factoring is a mathematical method of breaking down a polynomial into its factors to simplify the expression. In the script, the instructor factors the velocity equation to make it easier to determine the sign of the velocity at T equals 2.5, which helps in understanding if the particle's speed is increasing or decreasing.

💡Speed

Speed is the magnitude of velocity, a scalar quantity that indicates how fast an object is moving without considering the direction. The script discusses the particle's speed in relation to the signs of velocity and acceleration to conclude whether the particle is speeding up or slowing down.

💡Graph

In the context of the video, a graph is a visual representation of the particle's motion, with the velocity and acceleration functions plotted against time. The script refers to the velocity graph to determine intervals where the particle is moving to the right or left and when it is slowing down or speeding up.

💡Secant Line

A secant line is a straight line that intersects a curve at two or more points. In the script, the instructor calculates the equation of a secant line that passes through two given points on the velocity graph to find the exact time interval where the particle's velocity changes from negative to positive.

💡Average Velocity

Average velocity is the total displacement of an object divided by the total time taken. The script calculates the average velocity of the particle over the interval from T equals 1 to T equals 2, using the position function and the change in position over the change in time.

💡Direction of Motion

The direction of motion refers to the way in which an object is moving, either to the right or left on a graph or in a physical space. The script uses the sign of the velocity function to determine the direction of the particle's motion at different intervals of time.

💡Maximum Velocity

Maximum velocity is the highest value of velocity an object attains during its motion. The script analyzes the velocity function to find the maximum velocity on the interval from T equals 0 to T equals 3, which is a critical point in understanding the particle's motion.

💡Total Distance

Total distance is the overall path length traveled by an object, regardless of direction. In the script, the total distance the particle moves on the interval from 1 to 5 is calculated by considering the changes in direction and summing the absolute values of the displacements.

💡Acceleration Zero

When acceleration is zero, it indicates that the object's velocity is not changing, suggesting the object is at a constant speed. The script finds the time when the acceleration is zero to determine the velocity of the particle at that instant, which is a specific point of interest in the analysis.

Highlights

The video focuses on solving unit 5 homework problems 25 to 28 related to particle motion.

Problem 25 explores whether the speed of a particle defined by the function \( X(t) = t^3 - 9t^2 + 24t \) is increasing or decreasing at \( t = 2.5 \).

Velocity and acceleration are calculated by differentiating the position function to analyze the particle's speed at \( t = 2.5 \).

The velocity function \( V(t) = 3t^2 - 18t + 24 \) is factored to simplify the analysis without a calculator.

At \( t = 2.5 \), the velocity \( V(2.5) \) is found to be negative, indicating the speed is decreasing.

The acceleration function is derived and its sign at \( t = 2.5 \) is used to determine if the particle is speeding up or slowing down.

A contradiction is noted where both velocity and acceleration are negative, but the conclusion is that the particle is speeding up, which is incorrect.

Problem 26 involves determining intervals where a particle is moving to the right based on a velocity graph.

The particle is moving to the right on the intervals [0, 1] and [5.25, 7] as identified from the velocity graph.

An incorrect method is used to estimate the interval endpoint, suggesting the need for the equation of the velocity graph for precise calculation.

Problem 27 requires finding the average velocity of a particle on the interval [1, 2] using the position function \( P(t) = t^3 - 4t^2 - 3t + 1 \).

The total distance moved by the particle on the interval [1, 5] is calculated by considering direction changes.

The maximum velocity on the interval [0, 3] is determined by analyzing the velocity and acceleration graphs.

The particle's velocity when its acceleration is zero is calculated using the position function \( s(t) = -4\cos(t) - \frac{t^2}{2} + 10 \).

The time \( t \) when acceleration is zero is found by solving \( 4\cos(t) - 1 = 0 \) within the interval [0, π].

The velocity of the particle at the time of zero acceleration is calculated to be approximately 2.555.

Transcripts

Browse More Related Video

Calculus AB Homework 5.3: Position, Velocity, Acceleration

Rectilinear Motion or Particle Motion or Straight Line Motion!

2011 Calculus AB free response #1a | AP Calculus AB solved exams | AP Calculus AB | Khan Academy

Particle Motion Day 2

2004 AP Calculus AB Free Response #3

Calculus AB Homework 5.5: Particle Motion Practice

Related Tags

Particle Motion Calculus Problems Velocity Analysis Acceleration Graph Position Function Derivative Calculation Educational Content Mathematics Tutorial Homework Help Physics Concepts