Work Energy Principle
TLDRIn this AP Physics essentials video, Mr. Andersen explains the work-energy principle, focusing on kinetic energy, which is energy due to motion, calculated as one-half mv squared. He clarifies that work is the force applied over a distance, and it's equivalent to the change in kinetic energy. The video demonstrates how to calculate work done on an object and its direct relation to kinetic energy, using examples like a baseball and a cart. It also covers how to determine if energy is being added or removed by analyzing force direction and velocity changes. Andersen simplifies complex concepts with practical examples and emphasizes the importance of understanding work and energy in predicting kinetic energy changes.
Takeaways
- 🔋 Energy is defined as the ability to do work, specifically kinetic energy, which is energy due to motion.
- 📐 Kinetic energy is calculated using the formula \( \frac{1}{2}mv^2 \), where \( m \) is mass and \( v \) is velocity.
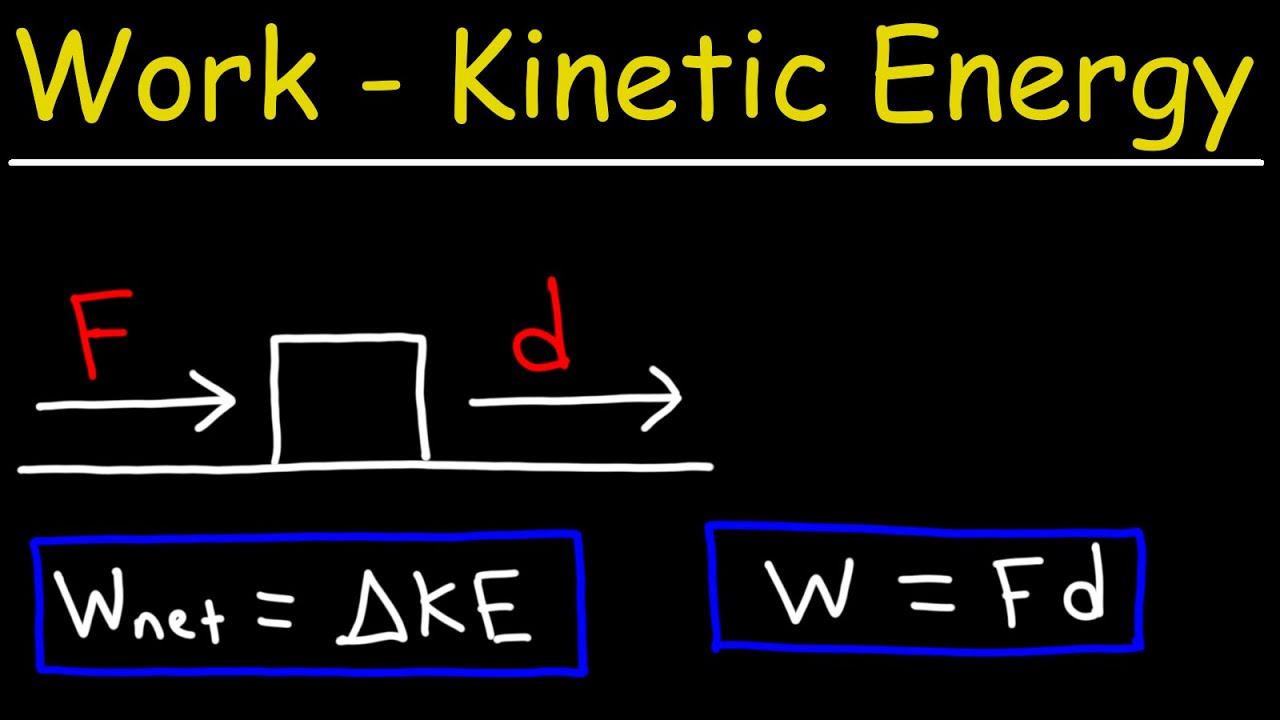
- 🏋️ Work is the product of force and distance over which the force is applied.
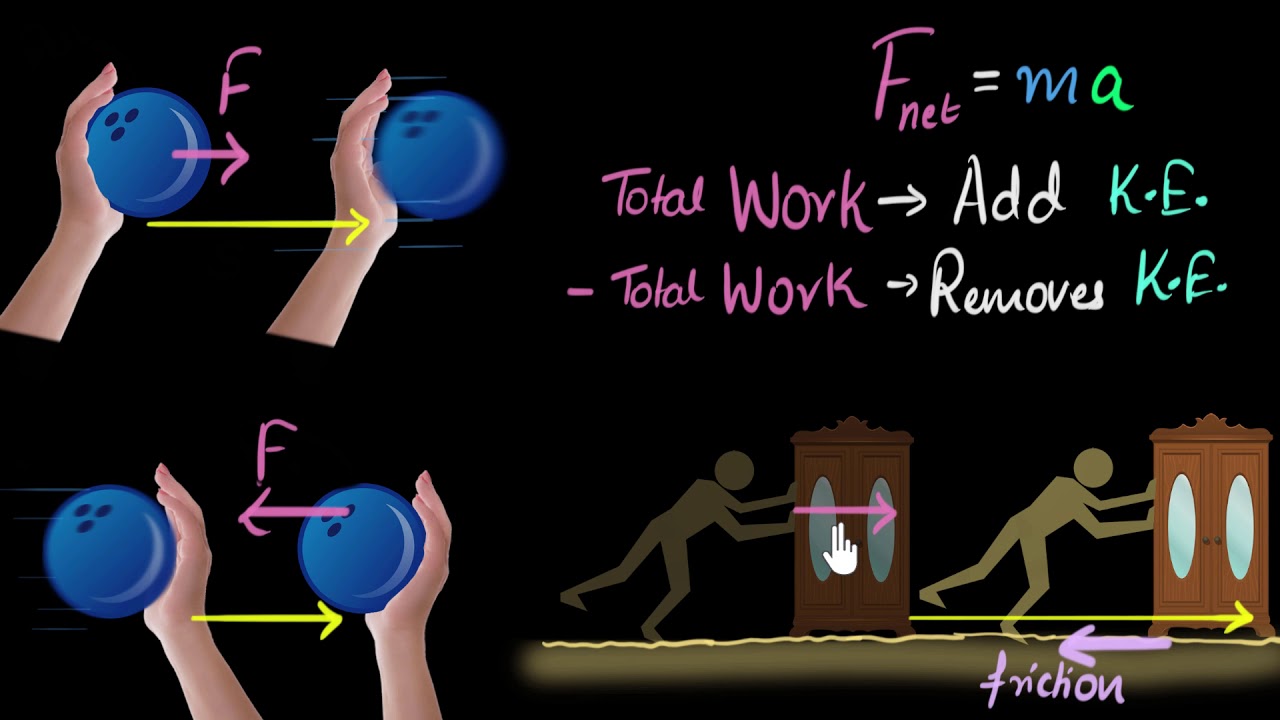
- ⚖️ Work and energy are equivalent; the work done on an object is equal to the change in its kinetic energy.
- ➡️ The direction of the force relative to the motion of the object determines whether energy is added or removed.
- ⏩ When force and motion are in the same direction, work is positive, and energy is added to the object.
- 🔙 Conversely, when force and motion are in opposite directions, work is negative, and energy is taken away.
- 📏 To calculate work done on an object moving at an angle, the force vector must be broken down into components parallel and perpendicular to the motion.
- 📐 Only the component of force parallel to the direction of motion contributes to work done on the object.
- 🧮 Work done on an object can be calculated using trigonometry when the force is applied at an angle, using the formula \( Work = Force \times Distance \times \cos(\theta) \).
- 🚀 The final kinetic energy of an object can be found by subtracting the initial kinetic energy from the final kinetic energy, which is equivalent to the work done.
- 🔧 Understanding the relationship between work, force, and kinetic energy allows for predictions about changes in an object's energy state.
Q & A
What is the definition of energy according to the video?
-In the video, energy is defined as the ability to do work, specifically kinetic energy which is the energy due to motion.
How is kinetic energy calculated?
-Kinetic energy is calculated using the formula \( \frac{1}{2}mv^2 \), where 'm' represents the mass of the object and 'v' represents its velocity.
What is the definition of work in the context of the video?
-Work is defined in the video as a force applied over a distance, and it is represented as the product of force and the distance moved in the direction of the force.
How are work and kinetic energy related in the video?
-The video explains that work and kinetic energy are equivalent; the amount of work done on an object is equal to the change in its kinetic energy.
What does it mean when work is positive?
-A positive work indicates that energy is being added to an object, causing it to accelerate or increase its kinetic energy.
What does it mean when work is negative?
-Negative work implies that energy is being taken away from an object, causing it to decelerate or decrease its kinetic energy.
How can you determine if energy is being added or taken away from an object?
-You can determine if energy is being added or taken away by looking at the direction of the force relative to the motion. If the force is in the direction of motion, energy is added (positive work). If the force is opposite to the motion, energy is taken away (negative work).
What is the significance of breaking down a force into its component vectors when calculating work?
-Breaking down a force into its component vectors is important because only the component of the force in the direction of motion contributes to the work done on the object.
How is the work done on an object calculated when the force is not aligned with the direction of motion?
-When the force is not aligned with the direction of motion, you calculate the work done by using the component of the force that is parallel to the direction of motion, which can be found using trigonometry (force parallel times distance times cosine of the angle).
What is the example given in the video to illustrate the calculation of work when the force is at an angle to the direction of motion?
-The video provides an example of a 9.6 newton force applied at a 32-degree angle from parallel to the direction of motion. The work done is calculated by multiplying the force by the distance and the cosine of the angle (9.6 N * 0.18 m * cos(32°)), resulting in 1.5 joules of work.
How does the video explain the concept of work-energy equivalence?
-The video explains the work-energy equivalence by demonstrating that the amount of work done on an object is equal to the change in its kinetic energy, which can be determined without directly calculating mass and velocity if the work is known.
Outlines
📚 Introduction to Work and Kinetic Energy
Mr. Andersen introduces the concept of work and energy in the context of AP Physics, focusing on kinetic energy. He defines energy as the ability to do work and specifies that the video will concentrate on kinetic energy, which is energy due to motion. The formula for kinetic energy is given as one-half times mass times velocity squared (1/2 mv^2), emphasizing that greater mass and velocity result in higher kinetic energy. Work is defined as the product of force and distance, and it's highlighted that work and kinetic energy are equivalent. The video uses the example of a baseball to illustrate how the work done by the pitcher is equivalent to the kinetic energy imparted to the ball.
🔧 Calculating Work and Kinetic Energy
The script explains how to calculate work and kinetic energy by applying a constant force over a distance, which results in the object gaining kinetic energy. It demonstrates the process with a simulation and discusses the concept of positive work, which adds energy to an object, and negative work, which removes energy. The importance of considering the direction of the force relative to the motion is highlighted, and the need to break down forces into their component vectors when they are not aligned with the direction of motion is emphasized. Examples are provided to illustrate how to calculate the work done on a cart moving horizontally with a force applied at various angles, using trigonometry to determine the component of force parallel to the motion.
Mindmap
Keywords
💡Work
💡Energy
💡Kinetic Energy
💡Mass
💡Velocity
💡Force
💡Distance
💡Equivalence
💡Component Vectors
💡Trigonometry
💡Cosine
Highlights
Introduction to the Work-Energy Principle and defining work and energy.
Definition of energy as the ability to do work, specifically kinetic energy due to motion.
Formula for kinetic energy: one-half mv squared, where m is mass and v is velocity.
Explanation of work as force times distance.
Equivalence of work and kinetic energy, always being equal.
Illustration of how work done by a pitcher gives kinetic energy to a baseball.
Calculating kinetic energy by calculating work done.
Demonstration of work done through a simulation with a constant force.
Qualitative analysis of adding or removing energy based on force direction.
Scenario of applying a net force opposite to motion, resulting in negative work.
Importance of considering force direction relative to motion when calculating work.
Example of calculating work done on a cart moving horizontally with a constant force.
Explanation of negative work done when force is applied in the opposite direction of motion.
Introduction of trigonometry for calculating work when force is at an angle to motion.
Calculation method using force, distance, and cosine of the angle to find work done.
Practical example of calculating work and energy added to a cart with a force at an angle.
Reinforcement of the concept that work done on an object is equivalent to the change in kinetic energy.
Encouragement to use force and velocity to predict changes in kinetic energy.
Conclusion summarizing the ability to calculate work and energy added to an object.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: