Riemann Hypothesis - Numberphile
TLDRIn this engaging conversation, Professor Frenkel and Brady delve into the complexities of the Riemann Hypothesis, one of the seven Millennium Problems with a $1 million reward for its solution. They explore the intriguing Riemann Zeta function, its relation to the sum of natural numbers, and its extension to complex numbers. The discussion highlights the function's critical strip and the hypothesis that all non-trivial zeros lie on a specific line, crucial for understanding prime number distribution. The connection between complex analysis and number theory is emphasized, showcasing the profound implications of the Riemann Hypothesis for mathematics.
Takeaways
- 💰 The most difficult ways to earn a million dollars include solving one of the Millennium Problems in Mathematics, set by the Clay Mathematical Institute in 2000.
- 📚 One of the Millennium Problems is 'The Riemann Hypothesis', which is related to the work of German mathematician Bernard Riemann from 1859.
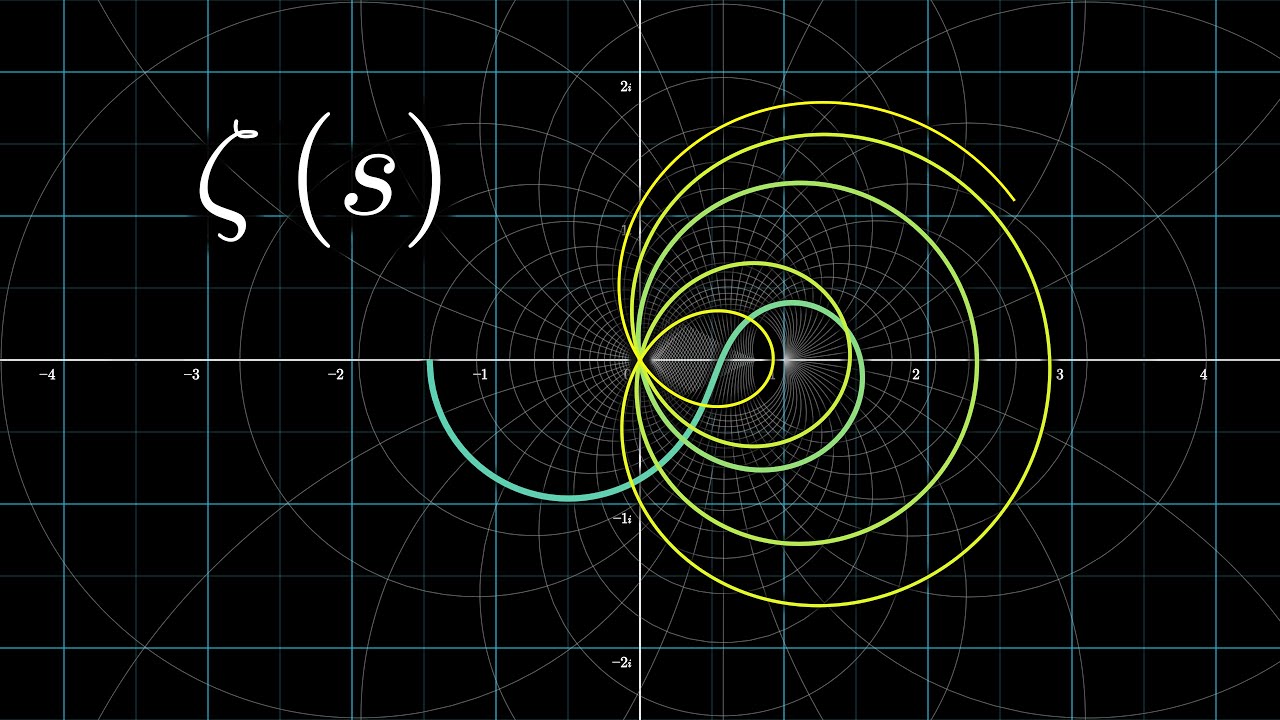
- 🧩 The Riemann Zeta function is a function that assigns a number to any value of 's' through a series, and it is central to the Riemann Hypothesis.
- 🔍 The Zeta function can be applied to various values of 's', including positive integers, leading to convergent series and interesting mathematical problems like the Basel problem.
- 📉 The Basel problem, solved by Leonhard Euler, is related to the sum of the reciprocals of the squares of natural numbers, which converges to π²/6.
- 🔄 Euler's proof connects the series to the circle constant π, demonstrating an unexpected relationship between the series and geometry.
- 🌐 Riemann extended the domain of the Zeta function to include complex numbers, allowing for the function to be defined for a broader range of 's', including those with real parts greater than 1.
- 🚫 The Zeta function has a singularity at s=1, where it cannot be defined, which is a unique exception in the complex plane.
- ❓ Riemann's hypothesis posits that all non-trivial zeros of the Zeta function lie on the critical line where the real part of 's' is 1/2, except for the trivial zeros at even negative integers.
- 🏆 A proof or disproof of the Riemann Hypothesis would earn a million-dollar reward, and it is a significant unsolved problem in mathematics.
- 🔗 The hypothesis is crucial because it underpins Riemann's formula for the distribution of prime numbers, linking complex analysis with number theory.
Q & A
What is the most difficult way to earn a million dollars according to Prof Frenkel?
-Prof Frenkel suggests that solving one of the Millennium Problems in Mathematics, such as the Riemann Hypothesis, is one of the most difficult ways to earn a million dollars.
What are the Millennium Problems?
-The Millennium Problems are seven mathematical problems that were established by the Clay Mathematical Institute in the year 2000, offering a one million dollar prize for a correct solution.
Who is Bernard Riemann and what is his contribution to the Riemann Hypothesis?
-Bernard Riemann was a German mathematician who conducted work in 1859 that led to the formulation of the Riemann Hypothesis, which is one of the unsolved Millennium Problems.
What is the Riemann Zeta function and how is it defined?
-The Riemann Zeta function is a complex function defined for complex numbers s with a real part greater than 1. It is given by the series 1/1^s + 1/2^s + 1/3^s + ..., where s is a complex number.
What is the significance of the Basel problem in the context of the Riemann Zeta function?
-The Basel problem, solved by Leonhard Euler, is significant because it found the sum of the reciprocals of the squares of the natural numbers, which is an example of the Riemann Zeta function for s=2, and it sums up to pi squared over 6.
How does the Riemann Zeta function handle the case when s is -1?
-When s is -1, the Riemann Zeta function yields the sum of all natural numbers, which is a divergent series. However, through analytic continuation, Riemann was able to assign a finite value to this case, which is -1/12.
What does it mean for a series to be convergent or divergent?
-A convergent series is one where the sum of its terms approaches a finite limit as more terms are added. A divergent series, on the other hand, does not approach a finite limit and its sum tends towards infinity.
What is the concept of analytic continuation in the context of the Riemann Zeta function?
-Analytic continuation is a method in complex analysis that allows the extension of the domain of a given analytic function beyond its initial domain of definition. Riemann used this concept to extend the Zeta function to all complex numbers except for s=1.
Why is the Riemann Hypothesis considered important in mathematics?
-The Riemann Hypothesis is important because it proposes that all non-trivial zeros of the Riemann Zeta function lie on the critical line with a real part equal to 1/2. This hypothesis, if proven, would have profound implications for the distribution of prime numbers.
What is the connection between the Riemann Zeta function and the distribution of prime numbers?
-Riemann's work showed that the zeros of the Zeta function are directly related to the distribution of prime numbers. His formula, which estimates the number of primes less than a given number, relies on the assumption that the Riemann Hypothesis is true.
What is the current status of the Riemann Hypothesis?
-As of the knowledge cutoff in April 2023, the Riemann Hypothesis remains unproven, despite extensive computational searches for zeros on the critical line and no counterexamples found.
Outlines
💰 The Challenge of Earning a Million via Solving Mathematical Problems
In this segment, Prof Frenkel and Brady discuss the difficulty of earning a million dollars, humorously comparing it to making YouTube videos. Prof Frenkel introduces the Millennium Problems, seven mathematical challenges set by the Clay Mathematical Institute in 2000, with one solved but the solver declined the reward. The conversation focuses on the Riemann Hypothesis, a famous unsolved problem related to the Riemann Zeta function. The Zeta function is explained as a series that assigns numbers based on a formula involving the reciprocals of increasing powers of s. The Basel problem, solved by Euler, is highlighted as an example of a convergent series summing to pi squared over 6. The segment also touches on the concept of divergent series, like the sum of all natural numbers, and how Riemann's work allows for assigning values to such series within the context of the Zeta function.
📚 Complex Numbers and the Expansion of the Zeta Function
This paragraph delves into the concept of complex numbers, which extend the real number line by introducing the square root of -1, denoted as 'i'. Prof Frenkel illustrates how complex numbers can be visualized on a plane, with real and imaginary parts. The discussion then returns to the Riemann Zeta function, explaining how Riemann extended its definition beyond its initial domain to include complex numbers. This analytic continuation allows the function to be defined for all complex numbers with a real part greater than 1, except at s=1, which is a singularity. The paragraph concludes with the intriguing fact that the Zeta function, when analytically continued, assigns a value of -1/12 to s=-1, effectively 'regularizing' the sum of all natural numbers.
🔍 The Search for Zeros and the Riemann Hypothesis
Prof Frenkel and Brady explore the concept of zeros of the Zeta function, which are the values of s for which the function equals zero. They note that while some zeros are trivially known (at even negative integers), the location of other zeros is a mystery central to the Riemann Hypothesis. The hypothesis posits that all non-trivial zeros lie on a critical line in the complex plane, specifically where the real part is 1/2. The paragraph explains the critical strip and the significance of finding zeros along the critical line, with the promise of a million-dollar reward for proving or disproving the hypothesis. The conversation highlights the extensive search for zeros and the trillions that have been found aligning with Riemann's prediction.
🔗 The Connection Between Zeta Function Zeros and Prime Number Distribution
In the final paragraph, the discussion shifts to the profound connection between the zeros of the Riemann Zeta function and the distribution of prime numbers. Riemann's work linked the two seemingly disparate areas of mathematics—complex analysis and number theory—by providing a formula that estimates the number of primes up to any given limit using the Zeta function. The importance of the Riemann Hypothesis is underscored, as the validity of this hypothesis is crucial for the accuracy of predictions about prime number distribution. The segment concludes by emphasizing the significance of this hypothesis in understanding a fundamental aspect of number theory.
Mindmap
Keywords
💡Millennium Problems
💡Riemann Hypothesis
💡Riemann Zeta function
💡Convergent series
💡Basel problem
💡Complex numbers
💡Analytic continuation
💡Singularity
💡Critical strip
💡Prime numbers
Highlights
The most difficult ways to earn a million dollars include solving one of the Millennium Problems in Mathematics.
The Riemann Hypothesis, set by the Clay Mathematical Institute in 2000, is one of the seven Millennium Problems.
The Riemann Hypothesis refers to the work of German mathematician Bernard Riemann from 1859.
Only one of the Millennium Problems has been solved, and the solver declined the one million dollar prize.
Mathematicians work on these problems for intellectual pursuit, not monetary gain.
The Riemann Zeta function assigns a number to any value of s through a specific series.
The Basel problem, solved by Leonhard Euler, is related to the Riemann Zeta function.
Euler's surprising solution to the Basel problem involves pi squared over 6.
The Riemann Zeta function can be extended to negative and complex numbers.
Riemann suggested that the Zeta function could assign a finite value to the divergent series of natural numbers.
Complex numbers are created by adjoining the square root of -1 to real numbers.
Riemann's insight allowed the Zeta function to be defined for all complex numbers with a real part greater than 1.
The Zeta function can be analytically continued to all complex numbers except for s = 1.
Riemann's hypothesis states that all non-obvious zeros of the Zeta function lie on the critical line.
The zeros of the Zeta function have a direct impact on the distribution of prime numbers.
Riemann's formula connects the Zeta function's zeros to the count of prime numbers up to any given number n.
The connection between the Zeta function and prime numbers is predicated on the Riemann hypothesis.
The Riemann hypothesis is crucial for obtaining deep results about the distribution of prime numbers.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: