The Riemann Hypothesis, Explained
TLDRThis script delves into the Riemann Hypothesis, a pivotal unsolved problem in mathematics with profound implications for prime number theory. Mathematician Alex Kontorovich guides viewers through the hypothesis's history, from Gauss's patterns in prime distribution to Riemann's extension of the Zeta function into the complex plane. The hypothesis, which posits that all non-trivial Zeta zeros lie on a critical line, could unlock the prime number distribution's secrets, with massive computational checks supporting but not proving it, highlighting the need for a rigorous mathematical proof.
Takeaways
- 🧩 The Riemann hypothesis is considered one of the most important unsolved problems in mathematics, with a significant impact on fields like cryptography and quantum physics.
- 🏆 It is one of the Millennium Prize Problems, offering a $1 million reward and a legacy in mathematics for its solver.
- 📚 The hypothesis is deeply connected to the distribution of prime numbers, a fundamental concept in number theory that has puzzled mathematicians for centuries.
- 🔍 The script introduces the concept of the Prime Counting Function, which graphically represents the distribution of prime numbers and was analyzed by Carl Friedrich Gauss.
- 🔑 Gauss's Conjecture, later connected to the Zeta function, suggested a relationship between the distribution of primes and the logarithmic integral function.
- 🤔 Euler's work on infinite series and the Zeta function hinted at a connection between the Zeta function and prime numbers, which was later expanded upon by Riemann.
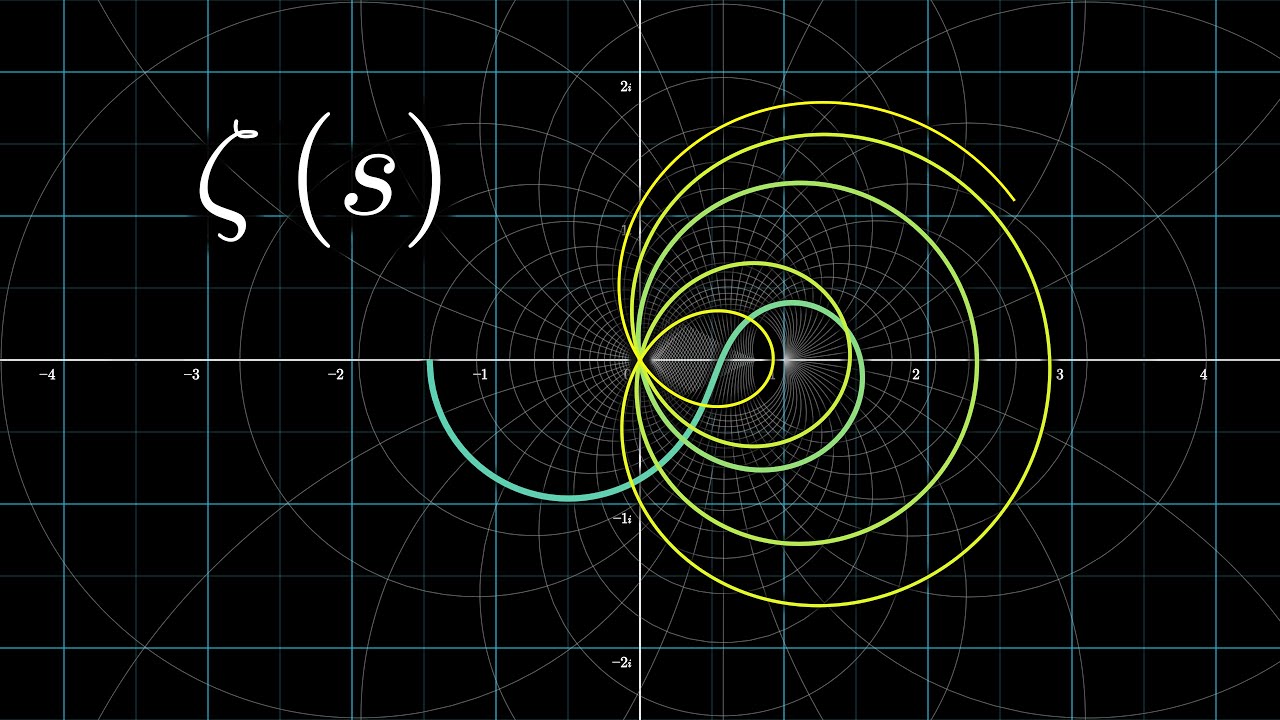
- 🌐 Riemann extended the Zeta function to the complex plane, allowing it to take complex inputs and revealing the existence of 'Zeta zeros'.
- 📉 The critical strip and the critical line are regions in the complex plane where the non-trivial Zeta zeros are hypothesized to reside, with the Riemann hypothesis stating they all lie on the line where the real part of 's' is 1/2.
- 🔍 Riemann's hypothesis, if true, would provide a precise prediction model for the distribution of prime numbers, as demonstrated by the connection between the Zeta zeros and the modified prime counting function.
- 💻 Despite extensive computational verification of billions of Zeta zeros aligning with the hypothesis, a rigorous mathematical proof is still required to confirm the hypothesis definitively.
- 📚 The script emphasizes the importance of a rigorous mathematical approach to solving the Riemann hypothesis, echoing the methods of the ancient Greeks.
Q & A
What is the Riemann hypothesis?
-The Riemann hypothesis is one of the most important unsolved problems in mathematics, which posits that all non-trivial zeros of the Riemann Zeta function lie on the critical line where the real part of the complex argument is one half.
Why is the Riemann hypothesis significant?
-The Riemann hypothesis is significant because it is related to the distribution of prime numbers, a fundamental question in number theory. If true, it could provide insights into the nature of primes and has implications in various fields such as cryptography and quantum physics.
What is the connection between the Riemann hypothesis and prime numbers?
-The Riemann hypothesis is connected to the distribution of prime numbers through the Riemann Zeta function. The hypothesis suggests that the zeros of this function, if all lie on the critical line, would allow for a precise prediction of the distribution of prime numbers.
What is the 'critical strip' in the context of the Riemann hypothesis?
-The 'critical strip' is a region in the complex plane where the real part of the complex argument of the Zeta function is between 0 and 1. The Riemann hypothesis is concerned with the location of non-trivial zeros within this strip.
What is the 'critical line' referred to in the Riemann hypothesis?
-The 'critical line' is a specific line within the critical strip where the real part of the complex argument is exactly one half. The Riemann hypothesis states that all non-trivial zeros of the Zeta function lie on this line.
What is the relationship between the Zeta function and the distribution of prime numbers?
-The Zeta function, particularly its zeros, is intimately connected to the distribution of prime numbers. Riemann discovered that the Zeta zeros could be used to adjust a function that approximates the prime counting function, suggesting a direct link between the zeros and the distribution of primes.
What is the significance of Euler's work on the Zeta function?
-Euler's work on the Zeta function was significant because he discovered that it could be expressed as an infinite product over all prime numbers, hinting at a deep connection between the Zeta function and prime numbers, which was later expanded upon by Riemann.
What is the 'Prime Counting Function' mentioned in the script?
-The Prime Counting Function is a function that counts the number of prime numbers less than or equal to a given number. It is used to visualize and understand the distribution of prime numbers in the set of natural numbers.
What is the 'logarithmic integral function' and how is it related to prime numbers?
-The 'logarithmic integral function' is a function whose slope is 1 over the logarithm of x. Gauss noticed that the graph of this function was similar to the graph of the Prime Counting Function, suggesting a connection between logarithmic properties and the distribution of prime numbers.
What is the significance of the 'harmonic series' in the context of the script?
-The 'harmonic series' is an infinite series of the reciprocals of the natural numbers. It is mentioned in the script to illustrate the concept of convergence and divergence of series, which is a fundamental concept in understanding the behavior of the Zeta function.
What is the 'analytic continuation' technique used by Riemann?
-Analytic continuation is a technique in complex analysis used to extend the domain of a function beyond its original convergence region. Riemann used this technique to extend the Zeta function to the entire complex plane, leading to the discovery of the Zeta zeros.
How has the Riemann hypothesis been tested so far?
-The Riemann hypothesis has been tested through computational methods, where billions of non-trivial Zeta zeros have been checked and found to align with the hypothesis. However, this does not constitute a mathematical proof, which is still required to confirm the hypothesis.
Outlines
🧩 The Enigma of the Riemann Hypothesis
This paragraph introduces the viewer to the Riemann hypothesis, one of the most significant unsolved problems in mathematics, which has haunted mathematicians for over a century and a half. It is highlighted as one of the millennium problems with a million-dollar prize attached to its solution. The hypothesis is deeply connected to the mystery of prime numbers, which are fundamental to various fields including cryptography and quantum physics. Alex Kontorovich, a professor of mathematics, offers to guide the audience through the complex world of the Riemann hypothesis, promising to explain advanced concepts in a visual and intuitive manner. The paragraph sets the stage for a journey into the chaotic realm of prime numbers, which are the building blocks of all numbers, and introduces the concept of the Prime Counting Function, which visualizes the distribution of primes.
📚 Euler and the Zeta Function's Connection to Primes
The second paragraph delves into the history of infinite series and their convergence, as explored by mathematicians like Euler. It discusses the concept of series and their limits, using examples to illustrate convergent and divergent series. Euler's discovery of the exact limit of the sum of the reciprocals of the squares of all positive integers, which is pi squared over six, is highlighted as a surprising connection between seemingly unrelated mathematical constants. Euler's further exploration into the Zeta function, which generalizes the series of reciprocals of integer powers, is explained. The function's convergence for values of s greater than one and Euler's groundbreaking revelation that the Zeta function can be expressed as an infinite product over prime numbers are central to this paragraph. The connection between the Zeta function and the distribution of prime numbers is introduced, setting the stage for Riemann's future contributions to this field.
🔍 Riemann's Extension of the Zeta Function and the Critical Line
In this paragraph, the focus shifts to Bernhard Riemann, who extended the Zeta function to the complex plane, a significant breakthrough that allowed the function to take on complex inputs. Riemann's use of analytic continuation to extend the Zeta function beyond its original domain is explained. The discovery of the Zeta zeros, points where the Zeta function equals zero, is introduced, with a distinction made between 'trivial' and 'non-trivial' zeros. The Riemann hypothesis is presented as the central claim that all non-trivial zeros lie on the critical line, where the real part of s is exactly one half. The paragraph explains the profound implications of this hypothesis for the understanding of prime numbers, suggesting that the distribution of primes is intimately connected to the location of these zeros.
🔢 The Computational Quest for the Riemann Hypothesis
The final paragraph discusses the ongoing efforts to prove the Riemann hypothesis, including a massive computing project that checked over 10 trillion non-trivial Zeta zeros, all of which aligned with the hypothesis. However, it emphasizes that computational verification, while extensive, cannot substitute for a rigorous mathematical proof, which remains the ultimate goal. The paragraph underscores the importance of a mathematical proof in confirming the Riemann hypothesis and its implications for number theory, as well as the enduring nature of this challenge, which echoes the methods of the ancient Greeks.
Mindmap
Keywords
💡Riemann Hypothesis
💡Prime Numbers
💡Complex Analysis
💡Zeta Function
💡Analytic Continuation
💡Critical Strip
💡Critical Line
💡Gauss's Conjecture
💡Logarithmic Integral Function
💡Euler
💡Riemann Zeta Function
Highlights
The Riemann hypothesis is one of the most important unsolved problems in mathematics.
It is one of the millennium problems of the Clay Institute, offering a 1 million prize for its solution.
The hypothesis is crucial for understanding the distribution of prime numbers, a fundamental mystery in mathematics.
Many theorems in cryptography and quantum physics assume the Riemann hypothesis to be true.
The search for a proof of the Riemann hypothesis has become a 'holy grail' for mathematicians.
Gauss's Conjecture, which relates the distribution of primes to the logarithmic integral function, is a precursor to the Riemann hypothesis.
Euler's work with infinite series and the Zeta function laid the groundwork for understanding the connection between prime numbers and the Zeta function.
Riemann extended the Zeta function to the complex plane, allowing for a deeper exploration of its properties.
The Zeta function's non-trivial zeros, if the Riemann hypothesis is true, all lie on the critical line where the real part of s is one half.
Riemann's hypothesis suggests that the distribution of prime numbers can be predicted through the location of non-trivial Zeta zeros.
A massive computing project has verified the Riemann hypothesis for the first 10 trillion non-trivial zeros.
The hypothesis remains unproven due to the inability to confirm it for an infinite number of zeros.
Riemann's work with complex analysis was foundational for Einstein's theory of relativity.
The critical strip and critical line are central concepts in the Riemann hypothesis, defining the region where non-trivial zeros are hypothesized to lie.
Riemann's hypothesis has profound implications for number theory and the understanding of prime numbers.
The connection between the Zeta function and prime numbers is a key aspect of the hypothesis.
Riemann's hypothesis could provide a complete understanding of the distribution of prime numbers if proven true.
The need for a rigorous mathematical proof to confirm the Riemann hypothesis remains, as brute force computation cannot resolve it.
Transcripts
Browse More Related Video

Riemann Hypothesis - Numberphile
But what is the Riemann zeta function? Visualizing analytic continuation

How Hard is an Oxford Maths Interview? Feat. Tom Rocks Maths

13 Pure Mathematics Books for Physicist's Entertainment

Oxford University Mathematician takes Admissions Interview (with @AnotherRoof)

Impossible Squares - Numberphile
5.0 / 5 (0 votes)
Thanks for rating: