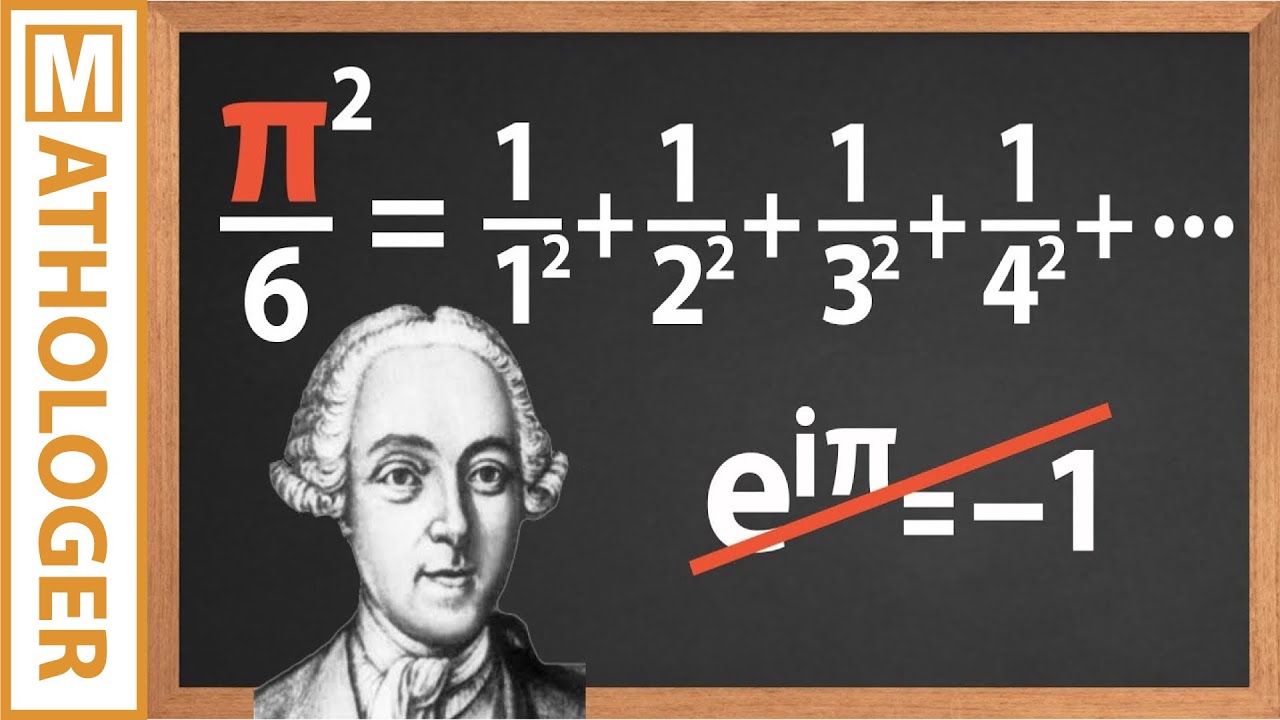But what is the Riemann zeta function? Visualizing analytic continuation

3Blue1Brown

9 Dec 201620:28

EducationalLearning

32 Likes 10 Comments

TLDRThe script delves into the complexities and beauty of the Riemann zeta function, a cornerstone in modern mathematics with implications for prime numbers and a million-dollar prize attached to its hypothesis. It explains the function's definition, its convergence for inputs greater than one, and the concept of analytic continuation which extends its domain beyond the initially defined range. The video also touches on the intriguing aspect of the zeta function mapping to zero at negative even integers and the critical strip where non-trivial zeros lie, hinting at the function's deep connection to the distribution of primes. The presentation aims to demystify the zeta function's role in mathematics and pique interest in the field of complex analysis.

Takeaways

🧩 The Riemann zeta function is a complex mathematical object central to modern mathematics, with its definition and properties linked to the unsolved Riemann hypothesis.
💡 The function is initially defined as an infinite sum for complex numbers with a real part greater than 1, where it converges to specific values, including intriguing connections to π².
🔍 The concept of analytic continuation is crucial for extending the zeta function beyond its initial domain, allowing it to be defined for all complex numbers except those with a real part of 1.
🌐 Analytic continuation is based on the property of angle preservation, meaning that the angles between intersecting lines remain unchanged after the transformation by an analytic function.
📉 The zeta function's extension to the left half of the complex plane is not defined by the original sum but through a unique analytic continuation that maintains the angle-preserving property.
💎 The Riemann hypothesis is an open problem offering a million-dollar prize for proving that all non-trivial zeros of the zeta function lie on the critical line where the real part of s is 1/2.
🔮 The zeros of the zeta function, both trivial and non-trivial, are significant as they encode information about the distribution of prime numbers, a mystery that has deep implications for number theory.
🎯 The trivial zeros of the zeta function are known to occur at negative even integers, and these are mapped to zero by the function's definition.
🌟 The visualization of the zeta function as a transformation of the complex plane provides a geometric understanding of its behavior and the impact of analytic continuation.
🤔 The script hints at the complex and abstract nature of deriving the extension of the zeta function, which while known to exist, remains partially mysterious in its details.
💬 The presentation aims to demystify some of the zeta function's aspects by providing visual and intuitive explanations, making the complex subject more accessible to a broader audience.

Q & A

What is the Riemann zeta function?
-The Riemann zeta function is a complex function that is significant in modern mathematics. It is defined for a given input 's' as the sum of 1 over each natural number raised to the power of 's'. This function is known for its deep connection to the distribution of prime numbers and its role in the unsolved Riemann hypothesis.
What is the Riemann hypothesis and why is it important?
-The Riemann hypothesis is an open problem in mathematics that proposes all non-trivial zeros of the Riemann zeta function have a real part equal to 1/2. It is important because it is related to the distribution of prime numbers and has implications for many areas of mathematics. A proof of this hypothesis would be worth a million dollars according to the Clay Mathematics Institute.
What is meant by 'analytic continuation' in the context of the Riemann zeta function?
-Analytic continuation refers to the process of extending the definition of an analytic function beyond its original domain. For the Riemann zeta function, it means defining the function for values of 's' where the original infinite sum does not converge, by ensuring the extended function remains analytic (preserves angles) everywhere.
Why is the sum of 1 plus 2 plus 3 plus 4 and so on said to equal negative one twelfth?
-This statement is derived through the use of analytic continuation and the Riemann zeta function. While the sum of natural numbers does not converge to any finite value, the zeta function can be analytically continued to negative integers, and it is found that zeta of negative one equals negative one twelfth.
What is the significance of the complex plane in understanding the Riemann zeta function?
-The complex plane is essential for visualizing and understanding the behavior of the Riemann zeta function, especially when considering complex numbers as inputs. It allows for the visualization of how the function transforms the input space and helps in understanding concepts like analytic continuation.
What is the role of complex exponentiation in defining the Riemann zeta function for complex inputs?
-Complex exponentiation is a method of extending the concept of exponents to complex numbers. It is crucial for defining the Riemann zeta function for inputs that are not just real numbers but complex numbers, allowing the function to be evaluated for inputs like '2 + i'.
How does the zeta function transform the complex plane when the real part of 's' is greater than 1?
-For inputs where the real part of 's' is greater than 1, the zeta function converges, and the transformation of the complex plane can be visualized as a spiraling movement towards a specific point, where the sum of the series converges to a value in the complex plane.
What is the meaning of the term 'trivial zeros' in the context of the Riemann zeta function?
-Trivial zeros of the Riemann zeta function refer to the zeros that occur at the negative even integers. These zeros are considered 'trivial' because they are well-understood and arise naturally from the properties of the function.
What is the critical strip and why is it significant in the study of the Riemann zeta function?
-The critical strip is a vertical strip in the complex plane that lies between the real parts 0 and 1. It is significant because it is the region where the non-trivial zeros of the zeta function, if they exist, are hypothesized to lie according to the Riemann hypothesis.
How does the concept of angles being preserved relate to analytic functions?
-Analytic functions are those that have a derivative everywhere, which geometrically means they preserve angles. When two lines intersect at a certain angle in the input space, after the transformation by an analytic function, they will still intersect at the same angle in the output space.

Outlines

00:00

🧩 Introduction to the Riemann Zeta Function

The video script introduces the Riemann zeta function, a complex mathematical concept with real-world implications, such as its relation to the Riemann hypothesis, a million-dollar unsolved problem in mathematics. The zeta function is initially defined for real numbers greater than one, where it sums the reciprocals of natural numbers raised to a given power s. The script hints at the function's deeper properties, including its connection to the sum of natural numbers and its extension to complex numbers, which involves the concept of analytic continuation. The explanation is aimed at those familiar with complex numbers but does not require calculus knowledge for understanding.

05:03

🌀 Visualizing the Zeta Function with Complex Numbers

The script delves into the visualization of the zeta function when extended to complex numbers, emphasizing the spiral convergence of the sum for inputs with a real part greater than one. It explains how raising a complex number to a power involves a rotation in the complex plane, preserving the sum's convergence but altering its path. The video aims to provide a visual representation of the zeta function's behavior across the complex plane, comparing it to simpler transformations like squaring a complex number. The script also discusses the limitations of the original sum definition and the necessity of analytic continuation to extend the function's domain.

10:04

🔍 The Beauty of Analytic Continuation

This paragraph explores the concept of analytic continuation, which allows for the extension of the zeta function beyond its initial domain of convergence. It discusses the restrictions imposed by requiring the extended function to remain analytic, meaning it must preserve angles at every point in the complex plane. The script uses the example of squaring a complex number to illustrate the angle-preserving property of analytic functions. It highlights the uniqueness of the extension that maintains analyticity, suggesting an intrinsic connection between the extended values and the original sum.

15:07

🎯 The Riemann Hypothesis and the Zeta Function's Zeros

The script introduces the Riemann hypothesis, which posits that all non-trivial zeros of the zeta function lie on the critical line where the real part of s is one half. This hypothesis is central to understanding the distribution of prime numbers and has significant implications for various mathematical fields. The video script explains the concept of trivial zeros at negative even integers and the critical strip where non-trivial zeros are believed to reside. It also mentions the visual evidence of the zeta function passing through zero multiple times, hinting at the potential validation of the Riemann hypothesis.

20:09

🔗 The Zeta Function's Connection to Infinite Sums and Prime Numbers

The final paragraph ties together the zeta function's properties with its implications for infinite sums and prime number theory. It discusses the surprising result that the zeta function, when analytically continued to the left half of the complex plane, assigns specific values to negative integers, such as mapping negative one to negative one twelfth. This connects back to the divergent sum of natural numbers and hints at a deeper relationship between the zeta function and the distribution of primes. The script concludes by emphasizing the uniqueness and significance of the analytic continuation process in defining the zeta function's behavior across the entire complex plane.

Mindmap

Keywords

💡Riemann zeta function

The Riemann zeta function is a complex function that has profound implications in number theory and is central to the unsolved problem known as the Riemann hypothesis. Defined originally for real parts greater than one, it sums over the reciprocals of natural numbers raised to a power s. The function is intimately connected with the distribution of prime numbers and is visualized in the script through its transformation of the complex plane, demonstrating its beauty and complexity.

💡Riemann hypothesis

The Riemann hypothesis is an unsolved problem in mathematics that offers a one million dollar prize for its solution. It posits that all non-trivial zeros of the Riemann zeta function have a real part equal to one half. The hypothesis is significant because it would provide a more precise understanding of the distribution of prime numbers, which is a fundamental aspect of number theory. The script discusses this hypothesis in the context of the zeta function's zeros and their importance.

💡Analytic continuation

Analytic continuation is a process in complex analysis that extends the domain of an analytic function beyond its original definition. In the script, it is used to define the Riemann zeta function for values outside the original domain where the function was defined by an infinite sum. The concept is crucial for understanding how the function can be extended to include negative values and complex numbers, and it is visualized through the transformation of the complex plane.

💡Complex numbers

Complex numbers are numbers that consist of a real part and an imaginary part, typically written as a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit with the property that i^2 = -1. In the context of the video, complex numbers are the inputs for the Riemann zeta function, and understanding them is essential for grasping how the function operates in the complex plane.

💡Complex analysis

Complex analysis is a branch of mathematical analysis that deals with functions of complex numbers. It was significantly developed by Bernhard Riemann, who is mentioned in the script. The study focuses on properties of analytic functions, which are complex functions that have a derivative at every point in their domain. The script discusses complex analysis in relation to the Riemann zeta function and its properties.

💡Complex exponentiation

Complex exponentiation refers to the operation of raising a number to a power that is a complex number. In the script, it is mentioned as a process that feels strange at first because it does not involve repeated multiplication as with real numbers. It is an essential concept for understanding how the Riemann zeta function operates with complex inputs.

💡Unit circle

The unit circle is a circle in the complex plane with a radius of one, centered at the origin. It is relevant in the script when discussing complex exponentiation, particularly when raising numbers like 1/2 to a pure imaginary power. The result lies on the unit circle, demonstrating the geometric interpretation of complex numbers.

💡Analytic function

An analytic function is a complex function that is locally given by a convergent power series. In the script, it is mentioned that the Riemann zeta function is analytic on the right half of the complex plane where the real part of s is greater than one. Analytic functions have the property of preserving angles, which is a key aspect of their behavior and is related to having a derivative at every point.

💡Trivial zeros

Trivial zeros of the Riemann zeta function are the zeros that occur at the negative even integers. The script mentions that these zeros are well-understood and occur at -2, -4, -6, etc., mapping to zero. The term 'trivial' in mathematics often refers to results that are considered straightforward or well-established, even if they are not immediately obvious.

💡Critical strip

The critical strip is a vertical strip in the complex plane that lies between the real parts 0 and 1. The script discusses how the non-trivial zeros of the Riemann zeta function, if they exist, must lie within this strip according to the Riemann hypothesis, which places them precisely on the critical line where the real part is 1/2.

💡Critical line

The critical line in the context of the Riemann zeta function is the line in the complex plane where the real part of s is exactly one half. The script explains that the Riemann hypothesis suggests all non-trivial zeros of the zeta function lie on this line, which has implications for the distribution of prime numbers.

Highlights

The Riemann zeta function is a complex mathematical object known for its difficulty and importance in modern math.

There's a million-dollar prize for solving the Riemann hypothesis, which concerns when the zeta function equals zero.

The zeta function can be used to define the sum of natural numbers in a seemingly nonsensical way, such as 1+2+3+... = -1/12.

Analytic continuation is a concept used to extend the definition of complex functions like the zeta function beyond their original domain.

Complex numbers and their properties are fundamental to understanding the zeta function and analytic continuation.

The zeta function is initially defined for inputs where the real part is greater than 1, where it converges.

For s > 1, the zeta function sums over natural numbers raised to the power of s, with interesting results like pi^2/6 for s=2.

The concept of complex exponentiation is crucial for extending the zeta function to complex inputs.

Raising a number to a complex power involves splitting it into real and imaginary parts and rotating on the unit circle.

Visualizing complex functions as transformations helps understand how inputs are mapped to outputs in the complex plane.

The zeta function can be visualized by transforming the complex plane, showing how inputs greater than 1 converge.

Analytic continuation allows extending the zeta function beyond the right half of the complex plane where it originally converges.

The requirement for a function to be analytic (angle-preserving) restricts how it can be extended, leading to a unique continuation.

The Riemann hypothesis suggests that all non-trivial zeros of the zeta function lie on the critical line with a real part of 1/2.

The zeta function's extension to the left half-plane is defined implicitly, through the process of analytic continuation.

The zeta function's extension implies that the sum of natural numbers can be mapped to -1/12, highlighting the function's complexity.

The zeta function's properties and its extension are deeply connected to the distribution of prime numbers.

Transcripts

Browse More Related Video

Riemann Hypothesis - Numberphile

The Riemann Hypothesis, Explained

Euler's real identity NOT e to the i pi = -1

How Hard is an Oxford Maths Interview? Feat. Tom Rocks Maths

BusCalc 19 Local and Global Extrema

Lecture 8 | String Theory and M-Theory

Related Tags

Riemann Zeta Complex Analysis Analytic Continuation Prime Numbers Infinite Sum Math Mystery Critical Line Zeros of Zeta Pi Squared Million Dollar Problem