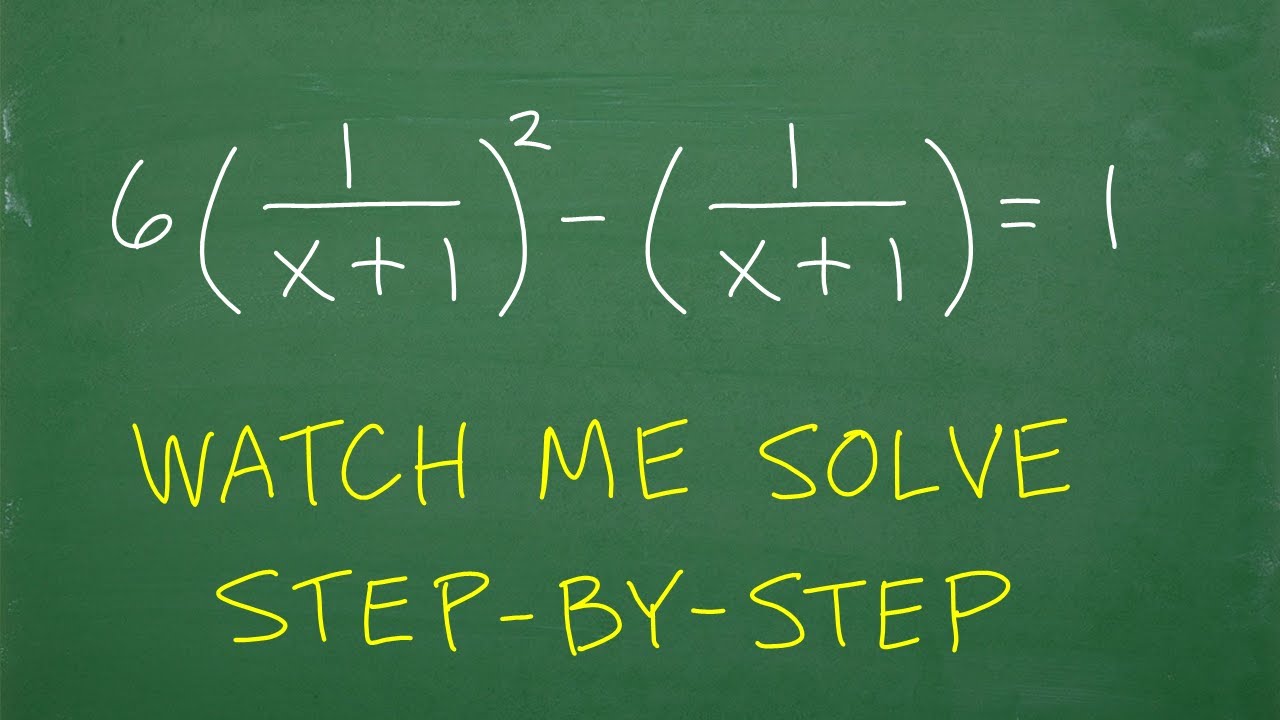Solve: the square root of (3x) = – 7 don’t make this common error!
TLDRIn this instructional video from TC Math Academy, John addresses a common mistake made when solving radical equations. He presents the equation √(3x) = -7 and clarifies that there is no solution, counter to what many might initially believe. John explains the concept of extraneous solutions and the importance of checking answers against the original equation. He emphasizes that the square root symbol refers to the principal (positive) root, not both positive and negative roots, which is a frequent point of confusion. The video serves as a valuable lesson for students studying algebra, highlighting the need for careful consideration when dealing with radical equations.
Takeaways
- 📚 The video is from John at TC Math Academy, focusing on solving a radical equation.
- 🔍 The equation presented is \( \sqrt{3x} = -7 \), which involves a square root (radical).
- ⚠️ John warns of a common mistake when solving such equations and encourages viewers to attempt solving it.
- 🔄 The video explains that the correct answer to the equation is 'no solution', indicating the null set.
- 📉 John emphasizes the importance of understanding extraneous solutions when squaring both sides of an equation.
- 📐 The video uses an example to illustrate how extraneous solutions can arise and why they need to be checked.
- 🤔 The script clarifies that when taking the square root of a number, the principal (positive) square root is typically considered.
- 📝 John demonstrates the process of squaring both sides of the equation and solving for x, leading to an incorrect solution.
- 🧐 The video highlights the misunderstanding that the square root of a positive number can be negative, which is not the case in real numbers.
- 📉 The script explains that the solution \( x = \frac{49}{3} \) is incorrect when checked against the original equation.
- 👍 The video concludes by encouraging viewers to like and subscribe for more math help, and to check out John's math courses.
Q & A
What type of equation is being discussed in the video?
-The video discusses a radical equation, specifically one involving a square root.
What is the radical equation presented in the video?
-The radical equation presented is √(3x) = -7.
What is the null set symbol represented in the video?
-The null set symbol, represented by a zero with a line through it, indicates that there is no solution to the equation.
What is the common error that the video warns viewers about?
-The common error the video warns about is incorrectly assuming that there is a solution to the equation when, in fact, there is none.
What is an extraneous solution in the context of radical equations?
-An extraneous solution is a value that appears to solve the transformed equation (after operations like squaring both sides) but does not satisfy the original equation.
What is the general approach to solving a radical equation?
-The general approach to solving a radical equation is to eliminate the square root, often by squaring both sides of the equation.
What is the difference between the principal square root and the square root when solving quadratic equations?
-The principal square root is the positive square root of a number, while when solving quadratic equations, both the positive and negative square roots must be considered.
Why is it incorrect to say that the square root of 16 is both +4 and -4 when just asking for the square root?
-It is incorrect because when asking for the square root of a number, the principal square root, which is the positive value, is implied. Only when solving quadratic equations should both the positive and negative roots be considered.
What is the result of squaring both sides of the equation √(3x) = -7?
-Squaring both sides results in 3x = 49, which simplifies to x = 49/3.
Why is x = 49/3 not a solution to the original equation?
-x = 49/3 is not a solution because when substituted back into the original equation, the left side does not equal the right side (the square root of 49/3 is not -7).
What is the conclusion of the video regarding the equation √(3x) = -7?
-The conclusion is that there is no solution to the equation √(3x) = -7 when working within the realm of real numbers.
Outlines
📚 Introduction to Solving Radical Equations
John from TC Math Academy introduces a video lesson focused on solving a specific radical equation: the square root of 3x equals negative seven. He emphasizes the importance of avoiding a common mistake when solving such equations. John invites viewers to participate by attempting to solve the equation and sharing their answers. He also promotes his math help program for various math-related needs and encourages viewers to like and subscribe for more content. The main theme is to educate viewers on how to correctly approach radical equations and understand the concept of extraneous solutions.
🔍 Understanding Extraneous Solutions in Radical Equations
The second paragraph delves into the concept of extraneous solutions when solving radical equations. John explains that squaring both sides of an equation can introduce solutions that do not satisfy the original equation. He uses a simple example where x equals 2 to illustrate how squaring both sides leads to a quadratic equation with two solutions, only one of which is valid when checked against the original equation. The paragraph aims to clarify the process of identifying and discarding extraneous solutions, highlighting the importance of checking all potential solutions in the context of the original equation.
🤔 Clarifying Misconceptions about Square Roots and Solutions
In the final paragraph, John addresses a common misconception regarding the square root of a number, particularly in the context of solving equations. He explains that the principal square root, which is the positive root, is the standard answer when taking the square root of a number, as opposed to including both positive and negative roots. This distinction is crucial when checking potential solutions for radical equations. John demonstrates how misunderstanding this concept can lead to incorrect conclusions about the validity of solutions. He emphasizes the need for careful consideration of principal square roots and the process of checking solutions to avoid extraneous solutions in algebra.
Mindmap
Keywords
💡Radical Equation
💡Square Root
💡Null Set
💡Extraneous Solutions
💡Principal Square Root
💡Quadratic Equation
💡Algebra
💡Common Error
💡Checking Solutions
💡Imaginary Numbers
💡Math Help Program
Highlights
Introduction to solving a radical equation involving the square root of 3x equal to negative seven.
Warning about a common error made when solving such equations.
Invitation for viewers to attempt solving the equation and share their answers.
Announcement of the correct answer: there is no solution to the equation.
Explanation of the 'null set' symbol indicating no solution exists.
Discussion on the importance of understanding radical equations in algebra.
Promotion of the math help program at tcmathacademy.com.
Explanation of the steps to solve a radical equation by eliminating the square root.
Introduction of the concept of 'extraneous solutions'.
Illustration of extraneous solutions with a simple equation x = 2.
Demonstration of solving a quadratic equation and the importance of checking solutions.
Clarification on the difference between principal square root and solving quadratic equations.
Common misunderstanding about the square root of a number versus solving an equation.
Detailed explanation of why the solution x = 49/3 is incorrect for the original equation.
Emphasis on the principal square root being the positive value only.
Final review and summary of the key points covered in the video.
Encouragement to like, subscribe, and check out the math courses offered.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: