Quadratic Formula – MOST COMMON MISTAKES!
TLDRIn this instructional video, math teacher John emphasizes the importance of mastering the quadratic formula for algebra students. He highlights common mistakes made when using the formula and provides a step-by-step guide to solving a quadratic equation. John also discusses the significance of the discriminant in determining the type of solutions and offers tips for avoiding errors, such as simplifying expressions and being disciplined in the approach to problem-solving. The video aims to help students improve their algebra skills and build confidence in tackling quadratic equations.
Takeaways
- 📝 Quadratic Formula Mastery: It's crucial for algebra students to master the quadratic formula to solve quadratic equations effectively.
- 🔍 Identifying Quadratic Equations: Recognize second-degree polynomial equations (highest power is two) to apply the quadratic formula correctly.
- 🎓 Two Solutions Expected: Quadratic equations always have two solutions, which can be real, imaginary, or complex numbers based on the discriminant.
- 📈 Factoring Before Formula: Students should attempt to factor quadratic trinomials before resorting to the quadratic formula, as it can simplify the process.
- 📋 Standard Form Requirement: Ensure the equation is in standard form (highest to lowest power on one side and zero on the other) to correctly identify and use a, b, and c values in the quadratic formula.
- 🔢 Double-Check ABC Values: Carefully identify a, b, and c from the quadratic equation and ensure their correct insertion into the quadratic formula to avoid errors.
- 🌟 The Discriminant's Role: The expression b^2 - 4ac, known as the discriminant, determines the nature of the roots (real, imaginary, or double roots) of the quadratic equation.
- 📚 Order of Operations: Follow the order of operations and simplify expressions step by step, especially when dealing with square roots and radicals.
- 🤔 Pop Quiz Engagement: Engage with the content by participating in pop quizzes to test understanding of the quadratic formula and its components.
- 📈 Simplification Importance: Always fully simplify your expressions to avoid losing marks and to ensure a clear understanding of the solution process.
- 🚫 Common Mistakes Highlighted: Be aware of the common mistakes made in solving quadratic equations, such as incorrect sign handling, rushing calculations, and lack of organization.
Q & A
What is the main focus of the video?
-The main focus of the video is to highlight common mistakes students make when using the quadratic formula and to provide tips on how to avoid these mistakes.
What is the quadratic formula?
-The quadratic formula is used to solve quadratic equations and is given by X = (-b ± √(b² - 4ac)) / (2a), where a, b, and c are coefficients of the quadratic equation ax² + bx + c = 0.
Why is it important to simplify the quadratic equation before applying the quadratic formula?
-It is important to simplify the quadratic equation before applying the quadratic formula to ensure that the coefficients a, b, and c are correctly identified, which is crucial for the accurate application of the formula.
What is the 'discriminant' in the context of the quadratic formula?
-The discriminant in the quadratic formula is the expression b² - 4ac. It determines the nature of the roots of the quadratic equation, indicating whether the solutions are real, complex, or repeated.
What are some alternative methods to the quadratic formula for solving quadratic equations?
-Alternative methods to the quadratic formula include taking the square root of both sides (for perfect squares), factoring the equation, and completing the square.
Why should students try factoring before using the quadratic formula?
-Students should try factoring before using the quadratic formula because it can be a simpler and quicker method to solve quadratic equations, and it is not necessary to use the quadratic formula if the equation can be easily factored.
What is a common mistake students make when plugging in values into the quadratic formula?
-A common mistake students make when plugging in values into the quadratic formula is not using parentheses correctly or rushing through the process, leading to incorrect substitution of values and subsequent errors in the calculation.
How does the video emphasize the importance of neatness and organization in solving quadratic equations?
-The video emphasizes that neatness and organization are crucial for avoiding mistakes and ensuring accurate calculations. It suggests that students who are not neat and organized are more likely to make errors and not catch them during the problem-solving process.
What advice does the speaker give to students who struggle with algebra and the quadratic formula?
-The speaker advises struggling students to review the basics, practice regularly, and consider taking courses or watching more educational videos to improve their understanding and avoid common mistakes.
What is the significance of the 'fundamental theorem of algebra' mentioned in the video?
-The fundamental theorem of algebra states that every non-constant single-variable polynomial equation has at least one complex root. In the context of the video, it implies that quadratic equations will always have two solutions, which can be real or complex.
Outlines
📘 Introduction to Quadratic Formula
The video begins with an emphasis on the importance of mastering the quadratic formula for students taking algebra. The speaker, John, introduces himself as a math teacher with decades of experience and shares his passion for making math easier. He challenges viewers to solve a quadratic equation without revealing the formula, promising to highlight common mistakes throughout the video.
🧠 Understanding Quadratic Equations
John explains the concept of a quadratic equation, highlighting that there are always two solutions, which can be real, imaginary, or complex. He discusses various techniques for solving quadratic equations, such as taking the square root, factoring, and using the quadratic formula. John stresses the importance of identifying the type of equation before applying the quadratic formula and reviews the fundamental theorem of algebra.
🚫 Common Mistakes in Solving Quadratics
The speaker identifies common mistakes students make when solving quadratic equations. These include not attempting to factorize quadratic trinomials before resorting to the quadratic formula and not putting equations into standard form correctly. John emphasizes the need for discipline and carefulness when identifying coefficients and plugging them into the formula.
🔢 Plugging in Values and Simplification
John demonstrates how to correctly plug values into the quadratic formula and warns against rushing through the process. He explains the importance of using parentheses and double-checking each step to avoid errors. The speaker also discusses the discriminant part of the formula and its significance in determining the type of solutions.
🌟 Simplifying the Quadratic Formula
The speaker continues to work through the quadratic formula, simplifying the expression step by step. He discusses the importance of simplifying square roots and radicals, especially when dealing with perfect squares. John shares techniques to avoid common mistakes, such as incorrect signs and incomplete simplification, and emphasizes the need for practice and discipline in mathematics.
🎓 Final Thoughts and Encouragement
In the concluding part, John summarizes the process of solving quadratic equations and encourages students not to get discouraged by the complexity of the steps. He offers reassurance that all mathematical skills are improvable with practice and persistence. John also promotes his math courses and YouTube channel for further learning and support.
Mindmap
Keywords
💡Quadratic Formula
💡Algebra
💡Mistakes
💡Standard Form
💡Factoring
💡Discriminant
💡Simplifying
💡Mathematical Discipline
💡Educational Content
💡YouTube Math
Highlights
The importance of mastering the quadratic formula is emphasized for students taking algebra courses.
Common mistakes made by students when using the quadratic formula are discussed to help avoid these errors.
An example quadratic equation is provided for viewers to test their understanding and solve.
The correct answer format for the example quadratic equation is shown, highlighting the need for proper simplification.
The quadratic formula is introduced as a solution for second-degree polynomial equations.
The fundamental theorem of algebra is mentioned, indicating that quadratic equations have two solutions.
Different techniques for solving quadratic equations are briefly reviewed, including factoring and completing the square.
The quadratic formula is presented in its general form, with a, b, and c representing specific coefficients.
The first mistake students make is not attempting to factor a quadratic trinomial before resorting to the quadratic formula.
The second mistake involves not putting quadratic equations into standard form before using the quadratic formula.
The importance of identifying correct a, b, and c values in the quadratic formula is stressed to avoid errors.
The use of parentheses when plugging values into the quadratic formula is recommended to prevent mistakes.
The concept of the discriminant (b^2 - 4ac) in the quadratic formula is introduced, explaining its significance in determining the type of solutions.
A pop quiz question about the discriminant is posed to engage viewers and test their understanding.
The process of simplifying the quadratic formula is demonstrated step by step, emphasizing the need for patience and accuracy.
The importance of double-checking work and being neat and organized when solving mathematical problems is highlighted.
A call to action for viewers to subscribe to the YouTube channel for more comprehensive learning resources is made.
The final, fully simplified solution to the example quadratic equation is presented, showing the correct application of the quadratic formula.
The video concludes with encouragement for students to improve their algebra skills by understanding and avoiding common mistakes.
Transcripts
Browse More Related Video

Learn The Quadratic Formula in 10 min
A pump can fill a pool in 10hrs. Another pump can fill it in 15hrs. Both pumps together will take?
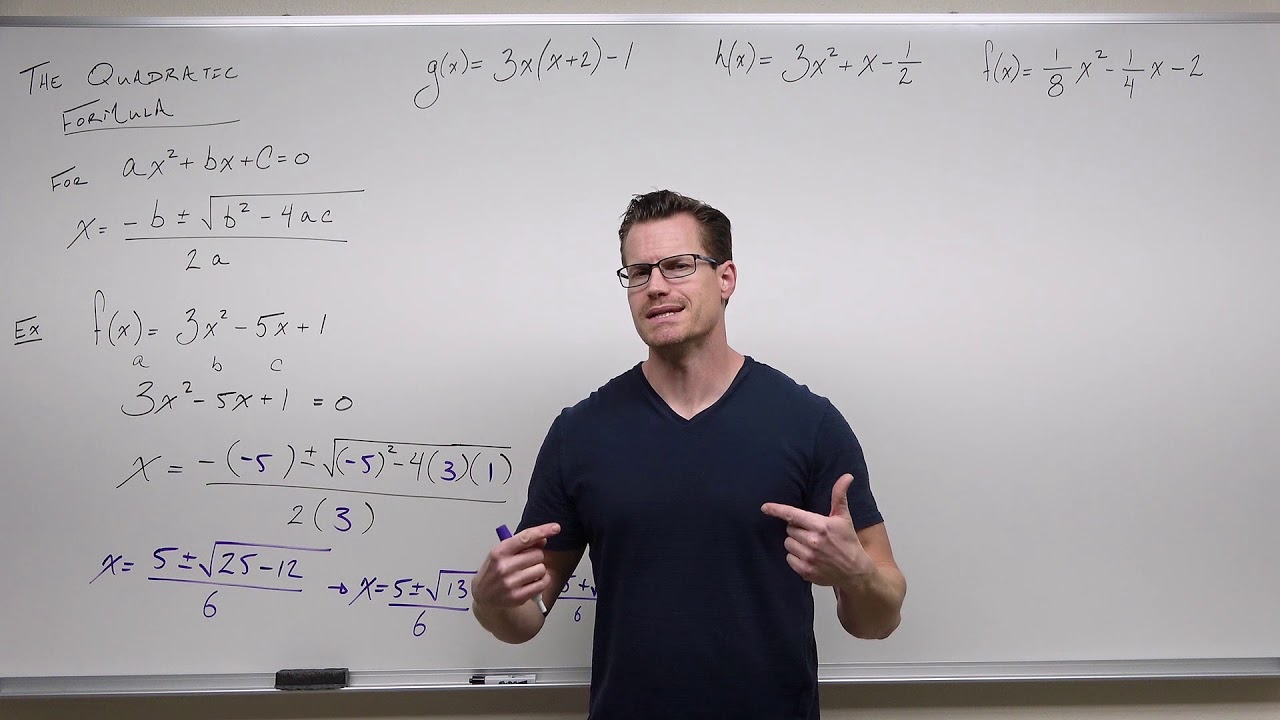
Using the Quadratic Formula (Precalculus - College Algebra 21)

Want to PASS Algebra? You better know this formula

The Algebra Step that EVERYONE Gets WRONG!

Terrible at Factoring trinomials? Do this…
5.0 / 5 (0 votes)
Thanks for rating: