Watch me solve this Rational Equation – step-by-step
TLDRIn this instructional video, John, a seasoned math teacher, guides viewers through solving a complex algebraic equation step by step. He emphasizes the importance of understanding the thought process behind each move, rather than just the final answer. John introduces the concept of a rational equation and explains how to find the lowest common denominator (LCD) to simplify the equation. He also warns about the potential for extraneous solutions when multiplying both sides of an equation by a variable expression. The video is a comprehensive guide to tackling algebraic challenges with patience and precision, highlighting the value of clear, structured problem-solving in mathematics.
Takeaways
- 📘 The video is focused on solving a complex algebraic equation step by step, emphasizing the thought process rather than the solution itself.
- 🧠 The speaker, John, highlights the importance of understanding the type of equation and the methods to solve it, rather than just finding the answer.
- 👨🏫 John, an experienced math teacher, stresses the value of his teaching approach in making math learning as easy as possible.
- 🔍 The process of solving the equation involves recognizing it as a rational equation, which is a key step in tackling the problem.
- 🧩 Finding the lowest common denominator (LCD) is crucial for solving rational equations, as it helps to eliminate fractions from the equation.
- ⚠️ The video warns about the potential introduction of extraneous solutions when multiplying both sides of an equation by an expression containing a variable.
- 📈 The equation is transformed into a quadratic equation, which is then solved by setting it to zero and moving terms around to get it into standard form.
- 📊 Factoring is identified as a critical skill for solving algebra, especially when dealing with quadratic trinomials.
- 🔎 Verification of solutions is necessary to ensure they are not extraneous roots, by plugging them back into the original equation.
- 📚 The importance of reviewing and mastering basic arithmetic and algebra skills is emphasized, as they are foundational for solving more complex problems.
- 💪 The video encourages persistence and discipline in learning math, emphasizing that with focus and practice, anyone can achieve success in mathematics.
Q & A
What is the main focus of the video?
-The main focus of the video is to provide insight into the thought process behind solving a specific algebraic equation, rather than just showing the solution. It aims to help viewers understand the tactics and methods used in solving algebraic problems.
What type of equation is being solved in the video?
-The equation being solved is a rational equation involving fractions and multiplication, with the form 6 * (1/x + 1)^2 - (1/x + 1) = 1.
What is the significance of the lowest common denominator (LCD) in solving rational equations?
-The lowest common denominator (LCD) is crucial in solving rational equations as it allows for the elimination of fractions by multiplying the entire equation by the LCD. This simplifies the equation and makes it easier to solve.
What is an extraneous solution in the context of solving equations?
-An extraneous solution is a solution that may arise when solving an equation by certain methods, such as multiplying both sides by a variable expression, but is not a valid solution to the original equation. It can be introduced when transforming the equation and must be checked and verified to ensure it is not an actual solution.
How can one verify a potential solution in a rational equation?
-To verify a potential solution in a rational equation, one must substitute the value back into the original equation and check if it satisfies the equation. If the left-hand side equals the right-hand side, the value is a valid solution; otherwise, it is an extraneous solution.
What is the final answer to the equation presented in the video?
-The final answer to the equation is x = -4 and x = 1. These are the solutions to the equation after it has been solved and extraneous solutions have been checked and ruled out.
What is the importance of showing all steps when solving a math problem?
-Showing all steps when solving a math problem is important because it allows for a clear understanding of the process, helps in identifying any mistakes or areas of confusion, and is essential for verifying potential solutions, especially in the case of extraneous solutions.
What does the video suggest about the learning process in mathematics?
-The video suggests that the learning process in mathematics involves a combination of understanding the concepts, practicing the skills, and being disciplined in showing work and checking solutions. It emphasizes the importance of focus, neatness, and structure in solving math problems and the necessity of reviewing and mastering foundational skills.
What resources does the speaker recommend for further learning and review in mathematics?
-The speaker recommends his own math program at TC maath academy.com for further learning and review. He also suggests checking out his Algebra 1 and Algebra 2 courses, as well as additional resources and videos on his YouTube channel for those who need help in specific areas of mathematics.
How does the speaker aim to help people with his YouTube channel?
-The speaker aims to help people by providing clear and understandable math instruction on his YouTube channel. His main mission is to prevent people from giving up on mathematics and to make learning math as easy as possible.
Outlines
📚 Introduction to Solving Algebraic Equations
The speaker, John, introduces himself as a math teacher with decades of experience and emphasizes the importance of understanding the thought process behind solving algebraic equations. He presents an equation to be solved and encourages viewers to share their answers. John also highlights the value of learning from mistakes and the significance of writing out all steps when solving math problems. He briefly discusses the type of equation presented, which involves fractions and rational expressions.
📈 Understanding Rational Equations and LCD
John delves deeper into the nature of the given equation, identifying it as a rational equation involving fractions. He explains the concept of rational numbers and the importance of finding the lowest common denominator (LCD) to simplify the equation. John warns viewers about the potential introduction of extraneous solutions when multiplying both sides of an equation by a variable expression and emphasizes the need for mastery in basic arithmetic to successfully handle such problems.
🔢 Transforming the Equation and Factoring
The speaker proceeds to transform the given equation by multiplying all terms by the LCD, resulting in a quadratic equation. He simplifies the equation and expresses it in standard form. John then discusses the various methods for solving quadratic equations, highlighting the benefits of factoring when possible. He demonstrates how the quadratic trinomial can be factored into two binomials and how the zero product property can be used to find potential solutions.
🔍 Verification of Solutions and the Importance of Arithmetic
John emphasizes the necessity of verifying the potential solutions found by factoring to ensure they are not extraneous roots. He substitutes the potential solutions back into the original equation to confirm their validity. The speaker also stresses the importance of being proficient in arithmetic and handling fractions, as these skills are crucial for verifying solutions and successfully solving more complex algebraic equations.
🎓 Encouragement for Persistence in Mathematics
In the concluding part, John encourages viewers to stay focused and disciplined when tackling algebra problems, emphasizing that with persistence and practice, anyone can achieve success in mathematics. He offers resources for further learning and reiterates the importance of neatness, structure, and thoroughness when solving problems. John concludes by wishing viewers well in their mathematical endeavors and thanking them for their time and participation.
Mindmap
Keywords
💡Algebra
💡Equation
💡Rational Equation
💡Lowest Common Denominator (LCD)
💡Extraneous Solutions
💡Quadratic Equation
💡Factoring
💡Zero Product Property
💡Verification
💡Mathematics Education
💡Math Skills
Highlights
The video aims to provide insight into the thought process behind solving algebraic equations, rather than just solving a specific equation.
The equation to be solved is 6 * (1/x + 1)^2 - (1/x + 1) = 1, with solutions being x = -4 and x = 1.
The instructor, John, has decades of experience teaching middle and high school math and focuses on making math learning as easy as possible.
The importance of writing out all steps when solving a math problem is emphasized to identify areas of understanding and misunderstanding.
The video introduces the concept of a rational equation, which involves fractions or rational expressions.
The lowest common denominator (LCD) is discussed as a critical technique for solving rational equations.
The potential for extraneous solutions when multiplying both sides of an equation by an expression with a variable is highlighted.
The process of simplifying the given equation by multiplying with the LCD (x + 1^2) is demonstrated.
The equation is transformed into a quadratic equation, emphasizing the need to be alert for extraneous solutions.
The quadratic equation is put into standard form by moving all terms to one side of the equation.
Factoring is introduced as a key skill for solving quadratic equations, with the importance of mastering it for algebra success.
The quadratic trinomial is factored into two binomials, leading to the use of the zero product property to find potential solutions.
Each potential solution must be checked and verified against the original equation to ensure they are not extraneous roots.
The verification process for the solutions x = 1 and x = 4 is demonstrated, showing how to reinsert the values into the original equation.
The video concludes with the verified solutions x = -4 and x = 1, emphasizing the importance of focus, discipline, and neatness in math problem-solving.
Transcripts
Browse More Related Video

The Algebra Step that EVERYONE Gets WRONG!
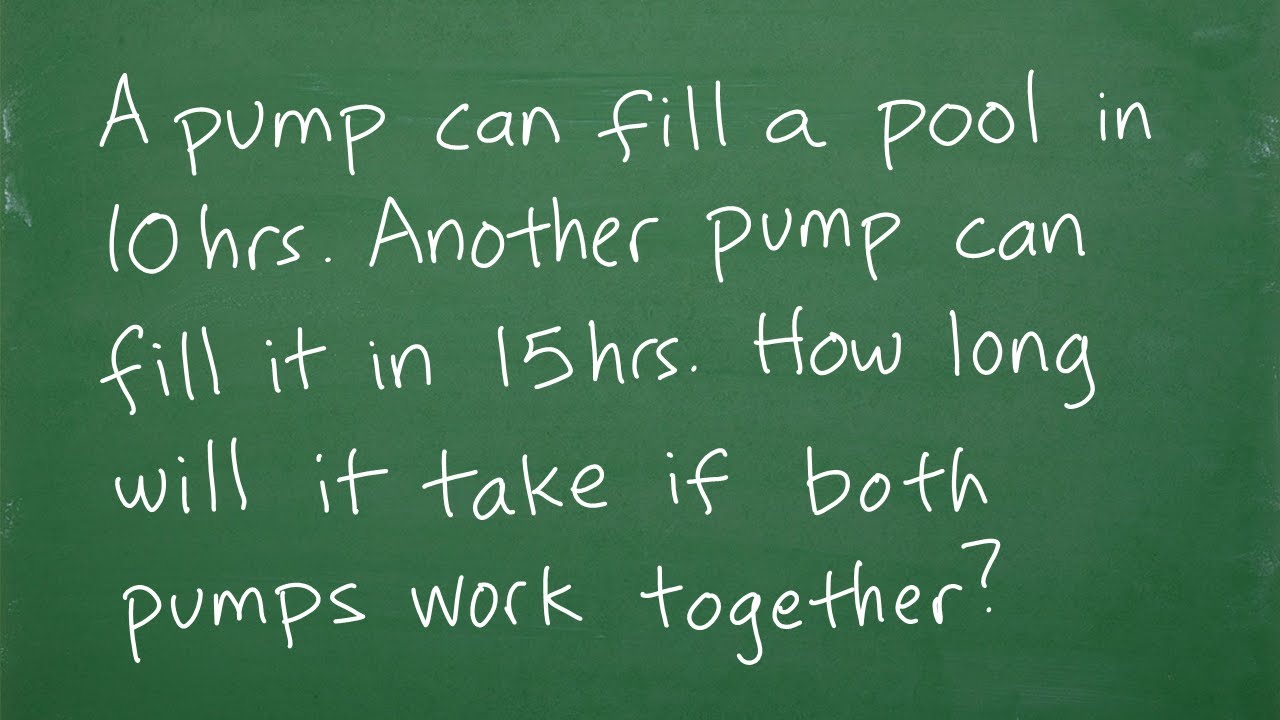
A pump can fill a pool in 10hrs. Another pump can fill it in 15hrs. Both pumps together will take?
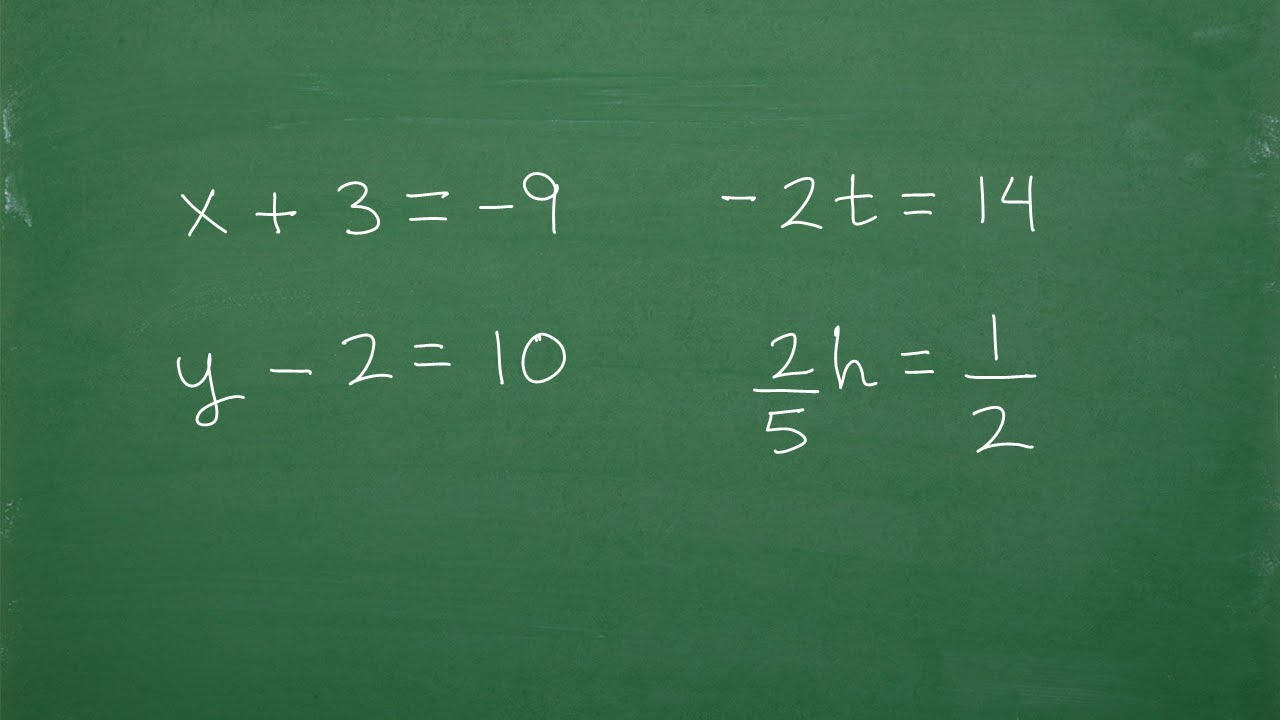
Let’s Solve These Basic Algebra Equations- Step-by-Step…….

Quadratic Formula – MOST COMMON MISTAKES!
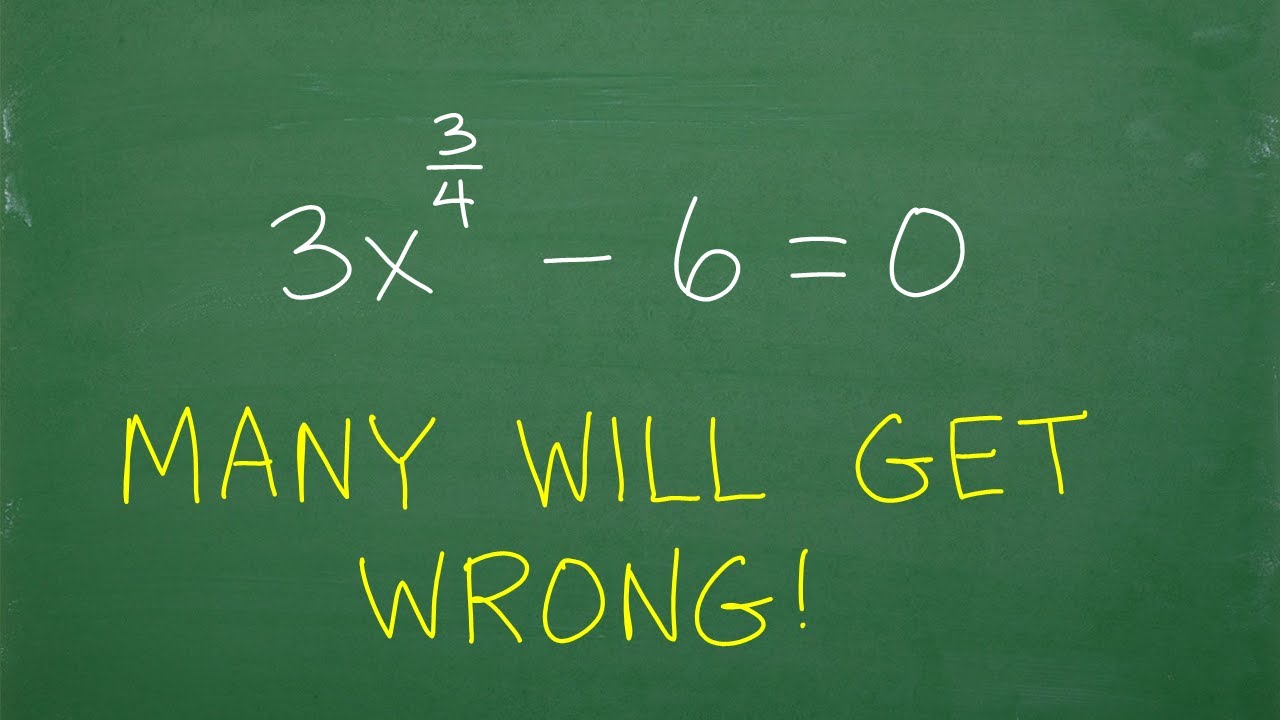
3x to the (3/4) power – 6 = 0, Many don’t know where to start…

3/2(x + 4) = 5 – 1/3(4 – x), many don’t know the EASY way to solve!
5.0 / 5 (0 votes)
Thanks for rating: