How to find Critical Numbers (Worked Examples)
TLDRThis educational video delves into the concept of critical numbers in calculus, essential for determining the shape of a graph. The host explains that critical numbers are points where the slope of a function changes sign or becomes undefined. The script guides viewers through finding critical numbers for various functions, including polynomials and rational expressions, using derivatives. It emphasizes the importance of simplifying expressions and applying the quotient and product rules, as well as the quadratic formula when necessary. The video aims to equip viewers with the skills to identify turning points and inflection points in functions, which are crucial for graph sketching and understanding the behavior of mathematical functions.
Takeaways
- 📚 Critical numbers are essential for understanding the behavior of a function's graph, particularly where the slope changes sign or becomes undefined.
- 📈 The concept of critical points is vital for sketching the graph of a function, as they indicate points of interest such as maxima, minima, or inflection points.
- 🔍 Critical numbers are found by calculating the derivative of a function and identifying where it equals zero or is undefined, which can indicate a change in the graph's slope.
- 📉 For polynomial functions, the derivative is unlikely to be undefined, so the focus is on finding where the derivative equals zero.
- 🤔 The presence of critical numbers can affect the shape of a graph, and without them, a graph may not exhibit any change in slope, indicating a consistently increasing or decreasing function.
- 📝 The script provides a step-by-step example of finding critical numbers for a cubic function, demonstrating the process of differentiation and solving for where the derivative equals zero.
- 🔢 The quadratic formula is used when the derivative of a function results in a quadratic equation, helping to find the critical numbers if they are real numbers.
- 🚫 The script clarifies that imaginary numbers derived from the quadratic formula do not qualify as critical numbers since they are not part of the real number line.
- 📐 The process of finding critical numbers involves both calculus (differentiation) and algebra (solving equations), and the script illustrates this with detailed examples.
- 💡 The importance of simplifying expressions and factoring is highlighted as a strategy to make the process of finding critical numbers more manageable.
- 👍 The script encourages continuous learning and the application of mathematical knowledge to solve problems related to finding critical numbers and sketching graphs.
Q & A
What is the main topic of the video?
-The main topic of the video is critical numbers in the context of graphing functions, explaining why they are important and how to find them.
Why are critical numbers important when sketching a graph of a function?
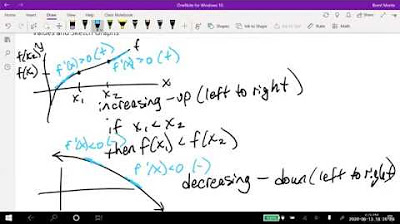
-Critical numbers are important because they determine the shape of the graph, especially where the slope of the curve changes sign or becomes undefined.
What is a critical point on a graph?
-A critical point on a graph is a point where the slope changes from negative to positive or from positive to negative, essentially where the sign changes.
What are the two conditions that make a number a critical number for a function?
-A number is a critical number for a function if the derivative of the function is either zero or undefined at that number.
How does the video define critical numbers for any function?
-The video defines critical numbers as the values of the input (x) for which the derivative of the function is zero or undefined.
What is the first example function given in the video, and what is its derivative?
-The first example function is f(x) = 2x^3 + x^2 + 2x. Its derivative, f'(x), is 6x^2 + 2x + 2.
Why does the first example function not have any critical numbers?
-The first example function does not have any critical numbers because the derivative, when set to zero, results in an imaginary solution, which is not on the real number line.
What is the quotient rule mentioned in the video, and when is it used?
-The quotient rule is a calculus rule used to find the derivative of a function that is the quotient of two other functions. It is used when differentiating a rational expression.
How does the video approach simplifying the derivative of the third example function?
-The video approaches simplifying the derivative of the third example function by factoring out common terms and using algebraic tricks to arrive at a rational expression.
What are the critical numbers for the third example function in the video?
-The critical numbers for the third example function are 0, 8/7, and 4, which are found by setting the factors of the simplified derivative equal to zero.
What is the significance of the quadratic formula in the video?
-The quadratic formula is used in the video to solve for x when the derivative of a function results in a quadratic equation, which is necessary to find critical numbers.
What is the conclusion given in the video about critical numbers?
-The conclusion given in the video is that critical numbers are essential for graphing functions and that they are the values of x for which the derivative is zero or undefined, and they must be real numbers.
Outlines
📚 Introduction to Critical Numbers in Graphs
The video begins with an introduction to critical numbers, emphasizing their importance in understanding the shape of a graph, especially for cubic functions. The instructor explains that critical numbers are points where the slope of the graph changes sign or becomes undefined. They illustrate this with examples of linear and cubic functions and highlight the need to identify these points when sketching graphs. The concept of critical points is further clarified as points where the slope changes from positive to negative or vice versa, which may occur multiple times or not at all. The video then transitions into a detailed exploration of how to find critical numbers through mathematical examples.
🔍 Finding Critical Numbers for Polynomial Functions
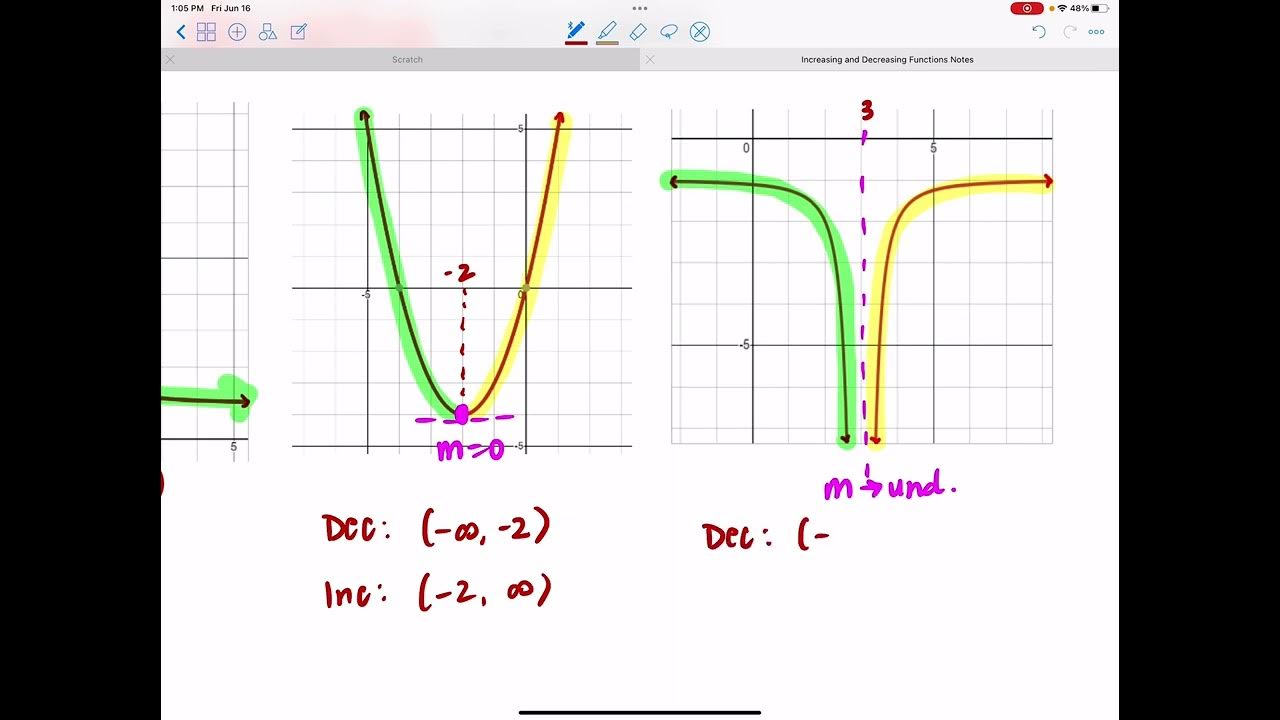
In this segment, the focus is on finding critical numbers for a given polynomial function. The derivative of the function is calculated, and the critical numbers are identified as the values of x for which the derivative is zero or undefined. The instructor demonstrates this process with a specific example, simplifying the derivative and applying the quadratic formula to find the critical numbers. They explain that if the derivative results in an imaginary number, it indicates that there are no real critical numbers, and thus the slope of the graph does not change, maintaining a consistent increase or decrease.
📈 Dealing with Rational Functions and Undefined Derivatives
The instructor moves on to rational functions, where the derivative can be undefined. They use the quotient rule to find the derivative and then set up conditions for finding critical numbers when the derivative is zero or the denominator is zero (which would make the derivative undefined). The example provided leads to an exploration of the quadratic formula and the realization that the bottom part of the rational expression can never be zero, indicating no undefined critical points. However, the top part can be zero, leading to potential real critical numbers, which are calculated using the quadratic formula.
🤔 Analyzing the Product Rule and Simplifying Expressions
This paragraph delves into the application of the product rule to find the derivative of a function that is a product of two other functions. The instructor simplifies the expression algebraically, factoring out common terms and using algebraic tricks to simplify the process. They emphasize the importance of simplifying to a rational expression to make it easier to find critical numbers. The goal is to have a clear top and bottom for the derivative, which allows for a straightforward determination of critical numbers when the derivative is zero.
📉 Identifying Critical Numbers Through Factoring and Simplification
The instructor continues with the process of simplifying derivatives and identifying critical numbers. They demonstrate how to factor out common terms and simplify the expression to find when the derivative equals zero. The example provided involves factoring out '2x - 4' and simplifying the expression to find the critical numbers, which are the values of x that make the top or bottom of the derivative zero. The result is a set of critical numbers that are real and can be used to understand the behavior of the graph.
👋 Conclusion and Encouragement to Continue Learning
In the concluding paragraph, the instructor summarizes the importance of finding critical numbers for any function, as they are essential for graphing and understanding the behavior of the function. They remind viewers that critical numbers are the values of the input for which the derivative is zero or undefined. The video ends with an encouragement to keep learning, as those who stop learning have stopped living, highlighting the ongoing journey of mathematical and intellectual growth.
Mindmap
Keywords
💡Critical Numbers
💡Linear Graph
💡Cubic Function
💡Slope
💡Derivative
💡Quotient Rule
💡Product Rule
💡Quadratic Formula
💡Factoring
💡Rational Function
Highlights
Importance of knowing critical numbers for sketching graphs of functions.
Critical numbers are essential for determining the shape of a graph.
Definition of critical points as points where the slope of a curve changes from negative to positive or vice versa.
Critical numbers are where the slope of a graph changes sign or does not exist.
Explanation of how to find critical numbers by taking the derivative of a function and setting it to zero or undefined.
Example of finding critical numbers for a cubic function where the derivative results in an imaginary number, indicating no critical numbers.
Illustration of how a graph without critical numbers will always have a consistent slope.
Demonstration of using the quotient rule to find critical numbers for a rational function.
Clarification that the bottom of a rational function cannot be zero, thus it is not a critical point.
Use of the quadratic formula to find real critical numbers for a given function.
Differentiation between critical numbers and solutions, emphasizing that critical numbers must be real.
Application of the product rule to find critical numbers for a function involving a product of two expressions.
Technique of factoring out common terms to simplify the process of finding critical numbers.
Final simplification leading to the identification of critical numbers for a complex function.
Conclusion on the necessity of knowing how to find critical numbers for graphing and understanding function behavior.
Encouragement to continue learning as it is integral to living.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: