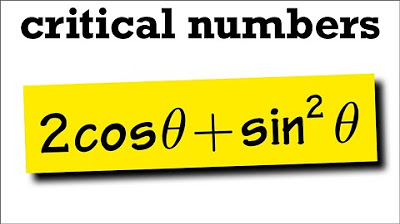How to Find Critical Values/Critical Numbers (Calculus 1) | Math with Professor V

Math with Professor V

13 Nov 202021:30

EducationalLearning

32 Likes 10 Comments

TLDRIn this informative Math TV video, Professor V guides viewers through the process of finding critical values or numbers for various functions. He emphasizes the importance of understanding the domain of a function and demonstrates how critical values can be derived from either where the derivative equals zero or where it does not exist. The video provides step-by-step examples using functions with different algebraic forms, applying the product rule and quotient rule for derivatives, and simplifying expressions to find critical points. Professor V also reminds viewers to exclude any critical values that fall outside the domain of the function. The tutorial is designed to help students with the computational aspect of calculus and encourages practice for mastery.

Takeaways

📚 The video is an educational resource on finding critical values or critical numbers in calculus.
🔍 Critical values are found by analyzing where the derivative of a function is equal to zero or does not exist.
📈 The domain of the function must be considered to ensure that critical values are within the valid input range.
📝 The process involves taking the derivative of the function, often using product or quotient rules for composite functions.
🧩 Factoring the derivative can simplify the process of finding where it equals zero or is undefined.
📉 Critical values are important for determining local maxima and minima, which are key concepts in calculus.
📌 The script provides step-by-step examples, demonstrating the mechanics of finding critical values for different types of functions.
📚 The video references a 'Calculus One' playlist for additional background information on the concept of critical values.
📐 The importance of listing the domain of the function at the beginning is emphasized to avoid including invalid critical values.
📝 The script concludes with a reminder to practice finding critical values to improve mathematical skills.
🔗 The video creator encourages viewers to like, subscribe, and watch more of their educational content.

Q & A

What is the purpose of the video by Professor V?
-The purpose of the video is to help viewers with the mechanics and computational aspect of computing critical values or critical numbers in calculus.
What are the two main sources of critical values or critical numbers?
-Critical values or critical numbers come from where the derivative f'(x) is equal to zero or where f'(x) does not exist.
Why is it important to consider the domain of the function when finding critical values?
-It is important to consider the domain because critical values must be within the domain of the function; otherwise, they are not valid for the function's analysis.
What is the domain of the function f(x) = x^(4/5) * (x - 4)^2?
-The domain of the function f(x) = x^(4/5) * (x - 4)^2 is all real numbers, as there are no restrictions from the terms involving roots or polynomials.
What rule is used to find the derivative of a function that is a product of two smaller functions?
-The product rule is used to find the derivative of a function that is a product of two smaller functions.
How does the process of finding critical values change when the function involves a natural logarithm?
-When the function involves a natural logarithm, the domain is restricted to x > 0, and the derivative is found using the quotient rule, considering the domain when determining critical values.
What is the domain of the function f(x) = ln(x) / x^4?
-The domain of the function f(x) = ln(x) / x^4 is (0, ∞), as x must be strictly greater than zero for the natural logarithm to be defined.
What is the difference between critical numbers and critical points?
-Critical numbers refer to the x-values where a function has a potential local extremum or point of inflection, while critical points include both the x and y values (x, f(x)) of these points on the function.
How does the process of finding critical values for a rational function differ from other types of functions?
-For a rational function, the domain must be considered to ensure the denominator does not equal zero, and the derivative is found using the quotient rule, with critical values determined by setting the numerator to zero or the denominator to zero, considering the domain.
What is the domain of the function f(x) = 16x / (x^2 + 16)?
-The domain of the function f(x) = 16x / (x^2 + 16) is all real numbers, as the denominator x^2 + 16 never equals zero.
What is the recommended approach to learn and understand the process of finding critical values?
-The recommended approach is to practice by pausing the video and attempting the examples on your own, then reviewing the provided solutions to enhance understanding.

Outlines

00:00

📚 Introduction to Finding Critical Values

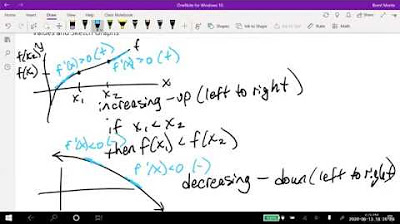
Professor V begins the video by introducing the topic of finding critical values or numbers, which are essential for understanding the behavior of functions in calculus. He emphasizes the importance of knowing the domain of the function and provides a link to a more detailed explanation from his Calculus One video lectures. Critical values are found by setting the derivative equal to zero or where the derivative does not exist. The video aims to help with the computational aspect of finding these values, and the first example involves a function with a domain of all real numbers, where the derivative is found using the product rule and simplified to find critical values.

05:02

🔍 Analyzing the Derivative for Critical Values

This paragraph focuses on the process of finding critical values by analyzing the derivative of a function. The professor illustrates how to simplify the derivative to a single term to make it easier to find where it equals zero or does not exist. The example given involves a function with a domain of all real numbers, and the derivative is simplified using common denominators and factoring. The critical values are found by setting the numerator of the derivative to zero and identifying where the denominator is zero, which are then checked against the domain of the function.

10:04

📈 Domain Considerations and Derivative Simplification

The professor discusses the importance of considering the domain of a function when finding critical values. He uses the example of the natural log function divided by x to the fourth, which has a domain restricted to x being greater than zero. The derivative is found using the quotient rule, and the critical value is determined by setting the numerator equal to zero, resulting in x equals e to the one-fourth. The professor reminds viewers to exclude values not in the domain when identifying critical values.

15:08

🌟 Critical Values in Rational Functions

In this section, the professor explores finding critical values in rational functions, specifically the function 16x over x squared plus 16. He explains that there are no domain restrictions due to the nature of the denominator, which never equals zero. The derivative is found using the quotient rule, and critical values are identified by setting the numerator equal to zero, yielding x equals plus or minus 4. The professor also notes that the denominator does not contribute to critical values since it has no real zeros.

20:10

📘 Practice Problem and Terminology Clarification

The professor presents a practice problem involving the function x to the one-third times x squared minus 63, encouraging viewers to pause the video and attempt the problem themselves. He then walks through the solution, using the product rule to find the derivative and identifying critical values by setting the numerator equal to zero. The professor also clarifies terminology, explaining the difference between critical numbers, critical values, and critical points, and how to report them depending on the context of the problem.

Mindmap

Keywords

💡Critical Values

Critical values, also known as critical numbers, are points on the graph of a function where the derivative is either zero or undefined. They are crucial in calculus for identifying potential local maxima or minima. In the video, Professor V explains how to find these values by setting the derivative equal to zero or finding where it does not exist, which is essential for analyzing the function's behavior.

💡Derivative

The derivative of a function measures the rate at which the function's output (or value) changes with respect to changes in its input. It is a fundamental concept in calculus and is used in the video to find critical values. For instance, when Professor V discusses finding critical values, he computes the derivative of functions like f(x) = x^(4/5)(x - 4)^2 and sets it equal to zero or checks where it does not exist.

💡Domain

The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. In the context of the video, Professor V emphasizes the importance of identifying the domain before finding critical values to ensure that the values found are within the valid range of the function. For example, the domain of f(x) = ln(x)/x^4 is all positive real numbers since the natural logarithm is undefined for non-positive values.

💡Product Rule

The product rule is a fundamental calculus theorem used to find the derivative of a product of two functions. In the video, Professor V applies the product rule when differentiating the function f(x) = x^(4/5)(x - 4)^2, which is a product of two separate functions. The rule states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function.

💡Quotient Rule

The quotient rule is a calculus theorem that allows for the differentiation of a quotient of two functions. Professor V uses the quotient rule in the video when finding the derivative of the function f(x) = ln(x)/x^4. The rule states that the derivative of a quotient is the derivative of the numerator times the denominator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.

💡Factoring

Factoring is a mathematical process of breaking down a polynomial or expression into a product of its factors. In the video, Professor V uses factoring to simplify expressions derived from applying the product and quotient rules. For example, when simplifying the derivative of f(x) = x^(1/3)(x^2 - 63), factoring helps to identify the critical values more easily by setting the factored numerator equal to zero.

💡Natural Logarithm

The natural logarithm, denoted as ln(x), is the logarithm to the base e (Euler's number, approximately equal to 2.71828). It is used in various mathematical and scientific contexts and appears in the video in the function f(x) = ln(x)/x^4. Professor V discusses the domain restrictions for ln(x), noting that x must be positive since the natural logarithm is undefined for non-positive values.

💡Chain Rule

The chain rule is a method in calculus for differentiating composite functions. Although not explicitly mentioned in the transcript, it is implied when Professor V discusses taking the derivative of (x - 4)^2, which involves differentiating the outer function squared and the inner function x - 4. The chain rule is essential for finding derivatives of complex functions where one function is composed of another.

💡Critical Points

Critical points are the points on the graph of a function where the function has a local maximum, local minimum, or a point of inflection. In the video, Professor V explains that critical values are the x-values where the derivative is zero or undefined, and these x-values can correspond to critical points when the y-values (f(x)) are considered along with them.

💡Rational Function

A rational function is a function that is the ratio of two polynomials. In the video, Professor V examines a rational function f(x) = 16x/(x^2 + 16) and discusses the domain considerations, noting that the denominator cannot be zero. Rational functions are a key topic in calculus, and their derivatives, as shown in the video, can reveal important information about the function's behavior.

Highlights

Introduction to finding critical values or numbers and their importance in calculus.

Explanation of where critical values come from: either where the derivative is zero or does not exist.

Emphasis on ensuring critical values are within the domain of the function.

Domain analysis for the function f(x) = x^(4/5) * (x - 4)^2.

Use of the product rule to find the derivative of a function composed of two smaller functions.

Technique for dealing with negative exponents by rewriting them as positive exponents.

Process of finding critical values by setting the numerator of the derivative equal to zero.

Identification of critical values where the derivative does not exist, by setting the denominator equal to zero.

Example of finding critical values for the function f(x) = ln(x) / x^4, including domain analysis.

Use of the quotient rule to find the derivative of a function with a quotient of two expressions.

Critical value determination for the function f(x) = ln(x) / x^4, with consideration of the domain.

Example of a rational function f(x) = 16x / (x^2 + 16) and its domain analysis.

Application of the quotient rule to find the derivative of a rational function.

Identification of critical values for a rational function by setting the numerator to zero.

Final example with function f(x) = x^(1/3) * (x^2 - 63), including domain and derivative calculation.

Clarification on terminology differences between critical numbers, critical values, and critical points.

Transcripts

Browse More Related Video

Math 11 - Section 3.1

finding the critical numbers of a rational function

How to find Critical Numbers (Worked Examples)

Find the critical numbers of 2cos(x)+sin^2(x)

Finding Absolute Extrema (Max/Min) on a Closed Interval [a, b]

Calculus 1: Relative Extrema Examples

Related Tags

Calculus Tutorial Critical Values Derivative Mechanics Product Rule Quotient Rule Math Education Critical Points Function Analysis Educational Content Professor V