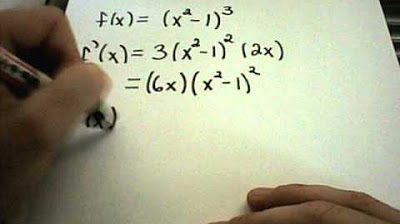Finding Critical Numbers

The Organic Chemistry Tutor
2 Mar 201821:19
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concept of critical numbers in functions, illustrating how to identify them through visual examples and step-by-step mathematical procedures. It explains that critical numbers occur where the derivative is zero or undefined, using local maxima, minima, and cusp points as examples. The script also covers cases where the function is not differentiable due to a zero in the denominator. Various examples are worked out, demonstrating the process of finding the first derivative, setting it to zero, and solving for x to determine the critical numbers. The importance of understanding the behavior of functions at these points is emphasized, as it is crucial for analyzing the function's overall structure and properties.

Takeaways
  • 📈 Critical numbers are values of 'x' where a function has a local maximum or minimum, or a point that is not differentiable.
  • 🤔 To find critical numbers, calculate the first derivative of the function and set it equal to zero, then solve for 'x'.
  • 🌟 At critical points, the function may have a horizontal tangent line, a cusp, or an abrupt change in slope.
  • 📚 If the function is a fraction, setting the numerator equal to zero can yield critical numbers where there's a horizontal tangent line.
  • 🔍 When dealing with a fraction, setting the denominator equal to zero gives critical numbers where the function is not differentiable.
  • 🛠️ For absolute value functions, the critical number occurs at the point where the inside of the absolute value is zero.
  • 📊 When working with trigonometric functions, use the chain rule and consider the periodic nature of the functions when finding critical numbers.
  • 🧩 For product rule functions, factor out the greatest common factor (GCF) before setting the numerator and denominator equal to zero.
  • 🔢 When solving for critical numbers, consider the domain of the function and discard solutions that fall outside of it.
  • 📐 Critical numbers are essential for understanding the behavior of a function, including its turning points and inflection points.
  • 🎓 Understanding critical numbers helps in analyzing the graph of a function, which is crucial for various applications in mathematics and its related fields.
Q & A

  • What are critical numbers in the context of a function?

    -Critical numbers are the values of the independent variable (usually x) within the domain of a function where the function has a local maximum, local minimum, or a point of non-differentiability such as a cusp or a horizontal tangent line.

  • How do you determine critical numbers for a given function?

    -To determine critical numbers, you first find the first derivative of the function. Then, you set this derivative equal to zero and solve for the independent variable (x). Additionally, you check for points where the derivative does not exist, as these points are also considered critical numbers.

  • What is the significance of a horizontal tangent line in a function?

    -A horizontal tangent line indicates a point where the slope of the function is zero. This can correspond to a local maximum, local minimum, or a point of inflection. The x-value at which this occurs is considered a critical number.

  • How does the numerator of a fraction become a critical number?

    -The numerator of a fraction becomes a critical number when it is set to zero, which can result in a horizontal tangent line on the graph of the function. This is because setting the numerator to zero can lead to a situation where the function has a zero in the numerator and a non-zero denominator, leading to a horizontal tangent line.

  • What happens when the denominator of a fraction is set to zero?

    -When the denominator of a fraction is set to zero, the function is not differentiable at that point. However, this x-value is still considered a critical number because it represents a point of discontinuity or a vertical tangent line on the graph of the function.

  • What is the role of the greatest common factor (GCF) in simplifying derivatives?

    -The GCF plays a crucial role in simplifying derivatives by allowing us to factor out common terms from both the numerator and the denominator. This simplification can make it easier to identify critical numbers by setting the simplified expression equal to zero and solving for the variable.

  • How do you find critical numbers for a function with an absolute value?

    -For a function with an absolute value, critical numbers occur at the points where the inside of the absolute value is equal to zero, as this is where the function is not differentiable. The slope of the function changes abruptly at these points, and the function has a vertical tangent line or a cusp.

  • What is the process for finding critical numbers in a function involving a square root?

    -To find critical numbers in a function involving a square root, you first differentiate the function using the appropriate rules (such as the product rule). Then, you set the derivative equal to zero and solve for the variable. For the denominator, you check for values that make the expression under the square root equal to zero, as these are the points of non-differentiability.

  • How do you handle trigonometric functions when finding critical numbers?

    -For trigonometric functions, you use the chain rule and the derivatives of the trigonometric functions (sine and cosine) to find the first derivative. Then, you set the derivative equal to zero and solve for the variable, keeping in mind the domain restrictions of the trigonometric functions.

  • What are the critical numbers for the function f(x) = |5x + 8|?

    -The critical number for the function f(x) = |5x + 8| is x = -8/5, as this is the value for which the inside of the absolute value equals zero, indicating a point of non-differentiability and a change in the slope of the function.

  • In the context of the video, what is the critical number for the function f(x) = 4x^3 - 15x^2 + 36x + 10?

    -The critical numbers for the function f(x) = 4x^3 - 15x^2 + 36x + 10 are x = 2 and x = 3, which are obtained by setting the first derivative f'(x) = 0 and solving for x.

Outlines
00:00
📈 Introduction to Critical Numbers

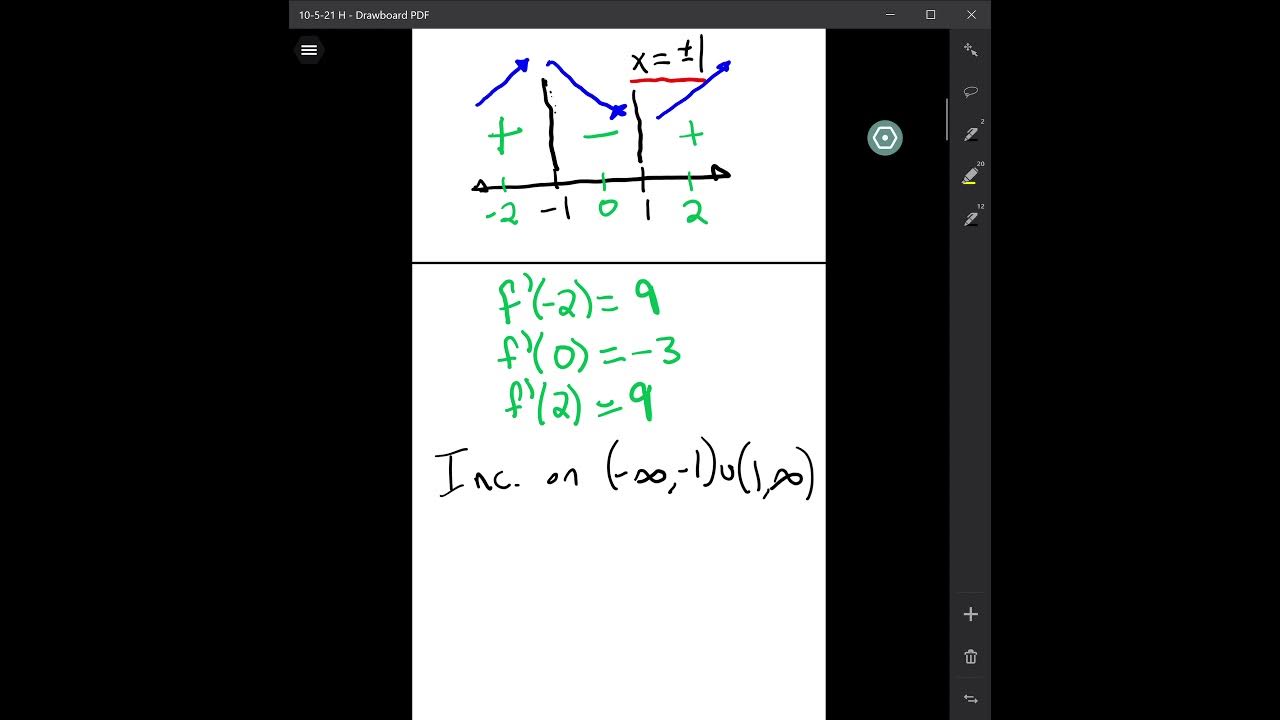
This paragraph introduces the concept of critical numbers in the context of a function. It explains that critical numbers are points where the function has a local maximum or minimum, a horizontal tangent line, or a cusp where the function is not differentiable. The importance of understanding critical numbers is emphasized, as they can indicate potential turning points or areas of interest in the function. The paragraph also touches on the topic of functions with zero in the denominator, where setting the numerator equal to zero yields a critical number with a horizontal tangent line, while setting the denominator to zero indicates a point of non-differentiability but still a critical number.

05:00
🧮 Solving for Critical Numbers

This paragraph delves into the process of finding critical numbers by calculating the first derivative of a function and setting it equal to zero. It provides a step-by-step explanation of how to find the derivative of a given function, using constant multiple rules and the power rule. The paragraph then illustrates this process with two examples, showing how to set up and solve equations to find the critical numbers. It emphasizes the importance of factoring out common factors and understanding how to deal with fractions in the context of derivatives.

10:02
📊 Working with Absolute Value and Trigonometric Functions

This paragraph focuses on identifying critical numbers in functions involving absolute values and trigonometric functions. It explains that the critical number for an absolute value function occurs at the point where the function is not differentiable, which is the middle of the 'V' shape. The process of finding critical numbers in such functions is demonstrated by setting the inside of the absolute value equal to zero. For trigonometric functions, the paragraph outlines the use of the chain rule and the importance of considering the function's restrictions, such as the periodic nature of sine and cosine. The examples provided illustrate how to find critical numbers by setting derivatives equal to zero and solving for the variable within the specified intervals.

15:08
🎓 Summary of Finding Critical Numbers

In this final paragraph, the process of finding critical numbers is summarized. It reiterates the importance of finding the first derivative of a function and setting it equal to zero to identify potential critical numbers. The paragraph also serves as a reminder that critical numbers can indicate points of interest in the function, such as local maxima, minima, or points of non-differentiability. The video concludes by encouraging viewers to practice finding critical numbers and to review related mathematical concepts if necessary.

Mindmap
Keywords
💡Critical Numbers
Critical numbers are points on a function where the derivative is either zero or undefined, indicating potential changes in the function's behavior. In the video, critical numbers are used to identify points of local maximum or minimum, as well as non-differentiable points such as cusps. For example, the video explains that at point 'c', there is a local maximum with a horizontal tangent line, and at point 'e', there is a cusp where the function is not differentiable.
💡Derivative
The derivative of a function represents the rate of change or the slope of the function at a given point. It is a fundamental concept in calculus used to analyze the behavior of functions. In the context of the video, finding the derivative of a function is the first step in determining critical numbers, as setting the derivative equal to zero helps identify potential maximum or minimum points.
💡Local Maximum/Minimum
A local maximum or minimum is a point on a function where the function reaches a peak or a trough within a certain interval, but not necessarily the absolute highest or lowest point on the entire function. In the video, these concepts are important for identifying critical numbers where the function's behavior changes from increasing to decreasing or vice versa.
💡Horizontal Tangent Line
A horizontal tangent line is a line that touches a function at a point and is parallel to the x-axis, indicating that the derivative of the function at that point is zero. This signifies a local extremum, where the function changes from increasing to decreasing or vice versa. In the video, the concept is used to explain why certain points are considered critical numbers.
💡Cusp
A cusp is a point on a curve where the function is not differentiable, meaning there is a sharp turn or a self-intersection. Despite being non-differentiable, a cusp is still considered a critical number because it represents a change in the function's behavior. In the video, point 'e' is an example of a cusp, which is a critical number even though its derivative does not exist.
💡Zero in the Denominator
When a function has a zero in the denominator, it implies that the function is not defined at that point, as division by zero is undefined in mathematics. However, this situation can still yield a critical number if the numerator is also zero, resulting in a horizontal tangent line. This is significant in the process of finding critical numbers, as it indicates a potential point of interest on the function.
💡Factoring
Factoring is the process of breaking down a polynomial into its constituent factors, which are simpler expressions that multiply together to give the original polynomial. This technique is crucial in solving equations and finding critical numbers, as it helps in setting the factors equal to zero to find the solutions.
💡Greatest Common Factor (GCF)
The greatest common factor (GCF) is the largest factor that two or more numbers share. In the context of the video, finding the GCF of terms in a polynomial is essential for simplifying expressions and factoring, which in turn helps in identifying critical numbers by setting the simplified expression equal to zero.
💡Power Rule
The power rule is a fundamental rule in calculus that states that the derivative of a function raised to a power is the power multiplied by the function, with the exponent decreased by one. This rule is used extensively in the video to find the derivatives of functions involving monomials, which is a crucial step in identifying critical numbers.
💡Chain Rule
The chain rule is a technique in calculus used to find the derivative of a composite function, which is a function made up of other functions. It involves differentiating the outer function with respect to the inner function and then differentiating the inner function. The chain rule is essential for finding critical numbers in more complex functions involving composite functions.
💡Trigonometric Functions
Trigonometric functions, such as sine and cosine, are mathematical functions that relate angles to real numbers. They are periodic and have specific values at certain angles. In the video, understanding the behavior of trigonometric functions is key to finding the critical numbers of the given function f(x) = sin^2(x) + cos(x) within a specific interval.
Highlights

The concept of critical numbers is introduced as part of understanding the behavior of functions.

Critical numbers are points where the function has a local maximum or minimum, or where it's not differentiable.

A visual illustration is provided to help understand critical numbers at various points of a function.

The importance of knowing critical numbers is emphasized for understanding the function's behavior and its applications.

A method for finding critical numbers is explained, which involves finding the first derivative and setting it equal to zero.

An example is given to demonstrate the process of finding critical numbers for a quadratic function.

The process of finding critical numbers is shown for a cubic function, highlighting the steps of differentiation and solving for x.

A detailed explanation of how to handle critical numbers in the presence of fractions and their impact on differentiability is provided.

The concept of a cusp and its relation to critical numbers is discussed, explaining points of non-differentiability.

The video provides a method for identifying critical numbers in absolute value functions by setting the inside of the absolute value equal to zero.

A comprehensive example involving a function with an absolute value and its critical number identification is presented.

The use of the product rule and chain rule in differentiation is demonstrated for finding critical numbers.

The video includes a step-by-step process for finding critical numbers in trigonometric functions, including the use of the chain rule.

The practical application of trigonometric functions and their critical numbers are discussed, with specific examples provided.

The video concludes by summarizing the method for finding critical numbers, reinforcing the importance of understanding the function's behavior.

Transcripts

Browse More Related Video

Relative Extrema

Finding Local Maximum and Minimum Values of a Function - Relative Extrema

3.1 - Using First Derivatives to Classify Max and Min Values

Finding Relative Extrema

Relative Maxima/Minima Examples

Increasing/Decreasing + Local Max and Mins using First Derivative Test

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsCalculusDerivativesCritical NumbersLocal ExtremaTrigonometryFunction AnalysisEducational ContentMath TutorialMathematics Education