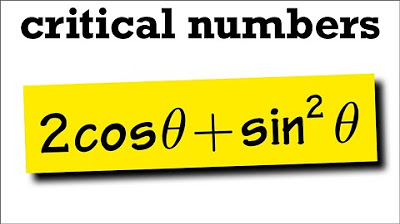Critical Points: Trigonometric Function

Laura Watkins
29 Mar 202113:37
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script guides viewers through the process of finding critical points of the function f(theta) = 2cos(theta) + sin(2theta). It explains the importance of considering where the derivative equals zero or is undefined. The script demonstrates how to derive the function and simplify it using trigonometric identities to solve for theta. It concludes by identifying critical points within a specific interval and extending the findings to the entire domain, providing a clear and concise explanation suitable for students learning calculus.

Takeaways
  • 🔍 The task is to find the critical points of the function f(θ) = 2cos(θ) + sin(2θ).
  • 📝 Critical points occur where the derivative of the function is zero or undefined.
  • 👉 The derivative of f(θ), f'(θ), is calculated as -2sin(θ) + 2cos(2θ).
  • 🚫 The derivative is defined for all real numbers, so there are no points where it is undefined.
  • 🧐 The focus shifts to finding θ where the derivative equals zero: -2sin(θ) + 2cos(2θ) = 0.
  • 🔄 A trigonometric identity is used to rewrite the equation in terms of a single trigonometric function.
  • 📈 The equation is simplified to 2sin²(θ) + sin(θ) - 1 = 0 by using the identity cos(2θ) = 1 - 2sin²(θ).
  • 🔢 The quadratic equation in terms of sin(θ) is factored to (2sin(θ) - 1)(sin(θ) + 1) = 0.
  • 📌 Two possible solutions for sin(θ) are derived: sin(θ) = 1/2 and sin(θ) = -1.
  • 📍 The critical points within the interval [0, 2π] are θ = π/6, 5π/6, and 3π/2.
  • 🌐 For the entire domain, the critical points are θ = π/6 + 2nπ, 5π/6 + 2nπ, and 3π/2, where n is an integer.
Q & A

  • What are critical points of a function?

    -Critical points of a function are the points where the derivative of the function equals zero or where the derivative is undefined.

  • What is the given function in the script?

    -The given function is f(theta) = 2cos(theta) + sin(2theta).

  • What is the derivative of f(theta)?

    -The derivative of f(theta), denoted as f'(theta), is -2sin(theta) + 2cos(2theta).

  • Why is it unnecessary to consider where the derivative is undefined for this function?

    -The derivative is defined for all real numbers since the function involves sines and cosines, which are defined for all real numbers.

  • How does the script approach solving the equation f'(theta) = 0?

    -The script uses a trigonometric identity to rewrite the equation in terms of a single trigonometric function, making it easier to solve.

  • Which trigonometric identity is used to simplify the equation involving cos(2theta)?

    -The identity used is cos(2theta) = 1 - 2sin^2(theta).

  • What is the resulting equation after applying the trigonometric identity?

    -The resulting equation is -2sin(theta) + 2(1 - 2sin^2(theta)) = 0.

  • How is the quadratic equation in terms of sine(theta) factored?

    -The quadratic equation 2sin^2(theta) + sin(theta) - 1 = 0 is factored into (2sin(theta) - 1)(sin(theta) + 1) = 0.

  • What are the solutions for theta when sin(theta) = 1/2?

    -The solutions for theta when sin(theta) = 1/2 are theta = pi/6 and theta = 5pi/6 within the interval from 0 to 2pi.

  • What is the critical point when sin(theta) = -1?

    -The critical point when sin(theta) = -1 is theta = 3pi/2 within the interval from 0 to 2pi.

  • How can the critical points be extended to the entire domain of f(theta)?

    -The critical points can be extended to the entire domain by adding integer multiples of 2pi to the critical points found within the interval from 0 to 2pi.

Outlines
00:00
📚 Introduction to Finding Critical Points

This paragraph introduces the concept of finding critical points of a function. It explains that critical points occur where the derivative of the function is zero or undefined. The function in focus is f(theta) = 2cos(theta) + sin(2theta). The speaker emphasizes that the derivative of the function, f'(theta), must be calculated first, which is done by differentiating each term and applying the chain rule where necessary. The derivative is found to be -2sin(theta) + 2cos(2theta). The paragraph concludes by stating that since the derivative is a trigonometric function, it is defined for all real numbers, thus the focus shifts to finding where the derivative equals zero.

05:00
🔍 Solving for Critical Points Using Trigonometric Identities

The speaker proceeds to solve for the critical points by setting the derivative equal to zero. They face a challenge due to the presence of both sine and cosine functions in the derivative. To simplify the equation, the speaker uses a trigonometric identity to express cos(2theta) as 1 - 2sin^2(theta), transforming the equation into one involving only sine of theta. The resulting equation is simplified and factored to yield two separate equations: 2sin(theta) - 1 = 0 and sin(theta) + 1 = 0. The solutions to these equations are then found within the interval from 0 to 2pi, leading to the identification of the critical points.

10:01
📈 Determining the Critical Points for the Given Interval

In this paragraph, the speaker identifies the specific critical points of the function f(theta) within the interval from 0 to 2pi. They find that sin(theta) = 1/2 corresponds to theta = pi/6 and theta = 5pi/6, and sin(theta) = -1 corresponds to theta = 3pi/2. These points are the critical points within the specified interval. The speaker then extends the discussion to the entire domain of the function, noting that the critical points will repeat every 2pi radians due to the periodic nature of trigonometric functions. The critical points on the entire domain are given as pi/6 + 2npi, 5pi/6 + 2npi, and 3pi/2, where n is an integer, representing the full rotations around the unit circle.

Mindmap
Keywords
💡Critical Points
Critical points are values of the variable where the derivative of a function is either zero or undefined. In the context of the video, the critical points of the function f(theta) are sought to understand the behavior of the function, such as its maxima or minima. The script discusses finding these points by setting the derivative equal to zero and solving for theta.
💡Derivative
The derivative of a function represents the rate at which the function's value changes with respect to its variable. In the video, the derivative of f(theta) is calculated to find critical points. The derivative is given by f'(theta) = -2sin(theta) + 2cos(2theta), and the focus is on where this equals zero.
💡Trigonometric Functions
Trigonometric functions, such as sine and cosine, are mathematical functions of an angle. In the video, the function f(theta) = 2cos(theta) + sin(2theta) involves both sine and cosine functions. These functions are fundamental in the analysis of the derivative and solving for critical points.
💡Undefined
In mathematics, a function is said to be undefined at certain points where it does not have a value. The script mentions checking for values of theta where the derivative is undefined, but since the derivative involves sine and cosine, it is defined for all real numbers, and no such points exist for this function.
💡Chain Rule
The chain rule is a fundamental principle in calculus used to compute the derivative of composite functions. In the video, it is applied to find the derivative of sin(2theta), where the derivative of the outer function (sin) is multiplied by the derivative of the inner function (2theta), resulting in 2cos(2theta).
💡Cosine of Two Theta
The term 'cosine of two theta' refers to the cosine function applied to twice the angle theta. In the video, it is part of the original function and its derivative. The script also discusses rewriting this term using trigonometric identities to simplify the equation and solve for critical points.
💡Trigonometric Identity
A trigonometric identity is an equation that holds true for all values of the variables involved and relates different trigonometric functions. The video uses the identity cos(2theta) = 1 - 2sin^2(theta) to rewrite the derivative and simplify the equation to a form that can be factored and solved.
💡Quadratic Equation
A quadratic equation is a polynomial equation of degree two. In the script, after applying the trigonometric identity and simplifying, the equation becomes quadratic in terms of sine(theta). The quadratic formula or factoring can be used to solve for theta, which is done in the video by factoring.
💡Factoring
Factoring is the process of breaking down a polynomial into a product of its factors. In the video, the quadratic equation in terms of sine(theta) is factored to (2sin(theta) - 1)(sin(theta) + 1) = 0, which allows for finding the critical points by setting each factor equal to zero.
💡Unit Circle
The unit circle is a circle with a radius of one, centered at the origin of a coordinate system. It is used in trigonometry to define sine and cosine functions in terms of angles. The video references the unit circle when determining the values of theta for which sine(theta) equals one-half or negative one.
Highlights

Introduction to finding critical points of a function by considering where the derivative equals zero or is undefined.

Derivative of the function f(theta) = 2cos(theta) + sin(2theta) is calculated as -2sin(theta) + 2cos(2theta).

The derivative is defined for all real numbers, indicating no undefined values.

Focus shifts to finding where the derivative equals zero.

Equation -2sin(theta) + 2(1 - 2sin^2(theta)) = 0 is derived from the derivative.

Use of trigonometric identity to simplify the equation to a single trigonometric function.

Rewriting the equation to involve only sine of theta terms.

Factoring the quadratic equation in terms of sine of theta.

Solving for sine of theta = 1/2 to find critical points.

Identifying critical points at theta = pi/6 and 5pi/6 within the interval [0, 2pi].

Considering the entire domain, critical points occur at pi/6 + 2npi and 5pi/6 + 2npi for integer n.

Critical point at theta = 3pi/2 is identified for the interval [0, 2pi].

Explaining the significance of adding 2pi to critical points to find all possible values on the entire domain.

Final critical points listed for the entire domain of f(theta).

Hope expressed for the helpfulness of the explanation provided.

Transcripts

Browse More Related Video

Critical Points: Square Root Function

Find the critical numbers of 2cos(x)+sin^2(x)

finding the critical numbers of a rational function

Find and classify critical points

How to Find Critical Values/Critical Numbers (Calculus 1) | Math with Professor V

Extrema on an Interval

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryCalculusCritical PointsDerivativeSine FunctionCosine FunctionChain RuleTrigonometric IdentityQuadratic EquationUnit Circle