Lecture 24: Calculus Everywhere
TLDRThis lecture celebrates the profound impact of calculus on our understanding of the world, highlighting its two fundamental concepts: the derivative and the integral. Originating from everyday observations, these ideas have evolved into a versatile tool for analyzing change and optimizing systems. The speaker illustrates the breadth of calculus applications, from the physical dynamics of a car to financial models and architectural structures. The video emphasizes the power of abstraction in calculus, showcasing how it offers a dynamic perspective on static objects and the intellectual conquest over infinity through limits and infinite processes. It concludes by recognizing the ongoing exploration and development of calculus, standing on the giants' shoulders of the past.
Takeaways
- 📚 Calculus is a fundamental and influential tool for quantitatively studying change and the relationship between parts and the whole.
- 🚗 The two main ideas of calculus, the derivative and the integral, were motivated by everyday observations such as a car moving on a road.
- 🛠️ Calculus is not a static subject; it continues to evolve with ongoing developments and applications in various fields.
- 🔍 The power of calculus lies in its ability to provide specific tools and a philosophy for interpreting the world through the lens of change.
- 🌡️ The heat equation, a differential equation, has broad applications, including in understanding engines and financial models.
- 💡 Infinite processes are central to calculus, as seen in the definitions of derivatives and integrals through the concept of limits.
- 📉 Infinite series allow for the representation of complex functions, like sine and cosine, as infinite polynomials, simplifying their manipulation.
- 🌟 The story of calculus can be viewed as the intellectual conquest of infinity, dealing with concepts like infinitesimals and limits.
- 🔄 Fractals, geometric shapes that are self-similar at different scales, challenge traditional calculus concepts by being nowhere differentiable.
- 🌐 Calculus has widespread applications across various disciplines, from physics and engineering to biology and finance.
- 👣 The development of calculus is an incremental exploration, building upon the work of past giants in the field, reflecting the ongoing nature of mathematical discovery.
Q & A
What are the two fundamental ideas of calculus?
-The two fundamental ideas of calculus are the derivative and the integral.
Why is calculus considered so effective in studying change?
-Calculus is effective in studying change because it provides the ability to quantitatively analyze how parts combine to make a whole and how things evolve over time.
How does calculus relate to the physical motion of a car's engine pistons?
-Calculus can be used to analyze the physical motion of a car's engine pistons through optimization problems associated with optimal fuel consumption and differential equations that describe the heating and cooling system.
What is the heat equation and how is it applied in various contexts?
-The heat equation is a differential equation that describes how heat dissipates through a medium, such as a rod or an engine block. It helps understand the way an engine works and has applications in various fields, including financial models like the Black-Scholes model for evaluating the cost of financial instruments.
How can calculus be applied to optimize the design of a dam?
-Calculus can be applied to determine the hydrostatic force on the wall of a dam and to solve optimization problems related to power generation, such as how to partition water among different turbines to maximize energy production.
What is an example of a calculus-based optimization problem in architecture?
-An example of a calculus-based optimization problem in architecture is determining the shape of a beam cut from a round log that will have maximum strength, by considering the relationship between the width and height of the beam.
How is calculus used in rocket science to optimize satellite placement?
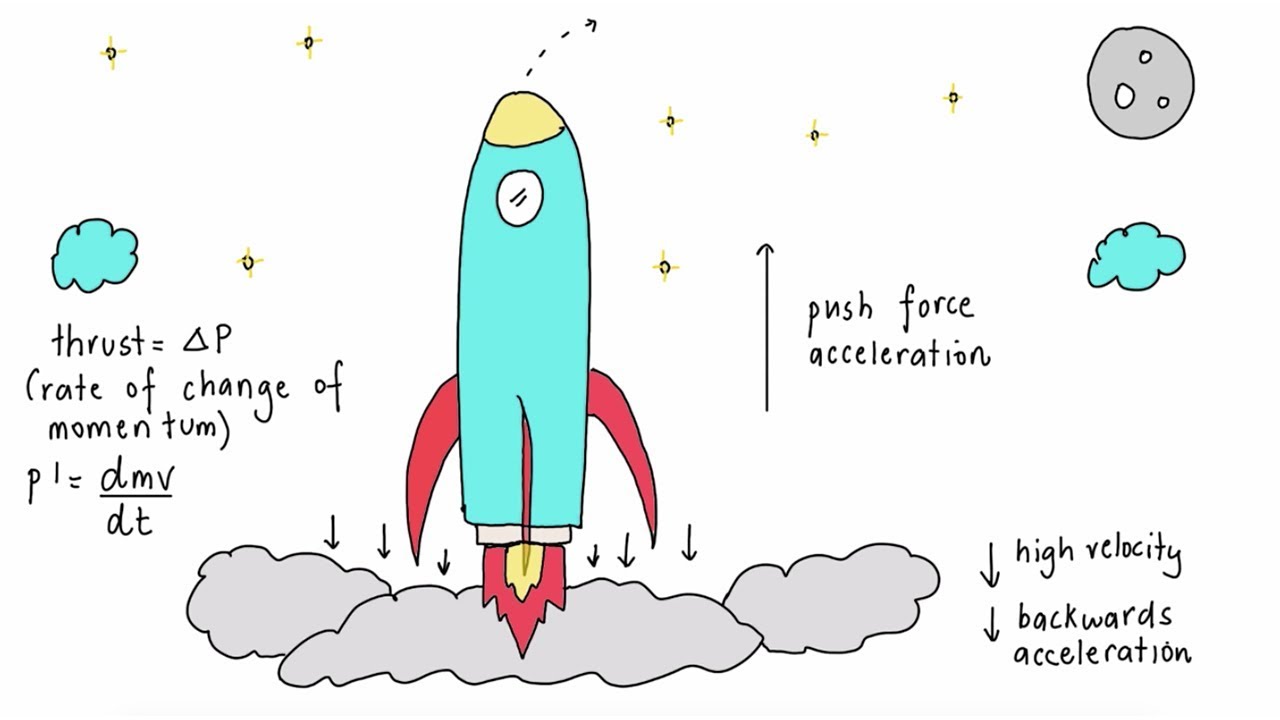
-In rocket science, calculus is used to optimize the division of fuel and the timing of jettisoning stages to minimize the mass of the rocket while achieving the desired velocity to get a satellite into orbit.
What is the significance of the limit concept in calculus?
-The limit concept is significant in calculus as it allows for the understanding of infinity and the resolution of paradoxes, such as Zeno's paradoxes, by taking snapshots at specific moments in time and combining them using a limit process.
How does calculus relate to the idea of infinite processes?
-Calculus is deeply connected to infinite processes through the use of limits, infinite series, and the concept of magnification to understand the behavior of functions and curves at an infinitesimal level.
What is a fractal and how does it challenge the traditional concepts of calculus?
-A fractal is a mathematical concept where objects look the same at every magnification level. Fractals challenge traditional calculus concepts because they can be nowhere differentiable, meaning they do not appear smooth upon magnification, which contradicts the fundamental premise of calculus that differentiable functions look like straight lines when magnified.
How did the development of calculus take thousands of years to mature?
-The development of calculus took thousands of years to mature because it required the accumulation of knowledge and the resolution of philosophical and mathematical challenges related to the concept of infinity and the development of rigorous mathematical techniques.
Outlines
📚 The Power and Evolution of Calculus
The speaker begins by emphasizing the profound impact calculus has had on our understanding and analysis of the world. They highlight the two foundational concepts of calculus: the derivative and the integral, which are derived from everyday observations but took centuries to fully develop. The speaker also points out that calculus is not a stagnant subject; it continues to evolve with new applications and extensions. The discussion then delves into specific applications of calculus, such as analyzing a car's motion, the physical workings of a car's engine, optimization problems related to fuel consumption, and the use of differential equations in understanding heating and cooling systems. The speaker also touches on how calculus has been applied to financial models, showcasing the versatility and ongoing relevance of calculus in various fields.
🔌 Applications of Calculus in Engineering and Science
This paragraph explores further applications of calculus in various fields, starting with electric circuits and moving on to hydrostatic force calculations for dam structures. The speaker discusses optimization problems, such as maximizing power generation from a dam with different turbines, and how calculus is essential in solving such problems. The summary also includes the use of calculus in determining optimal architectural structures, like suspension bridges and the strength of beams, through the optimization of shapes and materials. Product design is another area where calculus plays a crucial role, as seen in the example of minimizing material in a soda can while maintaining its function. The paragraph concludes by emphasizing the power of abstraction in calculus, which allows the same techniques to be applied across a wide range of disciplines.
🌐 The Dynamic Perspective of Calculus
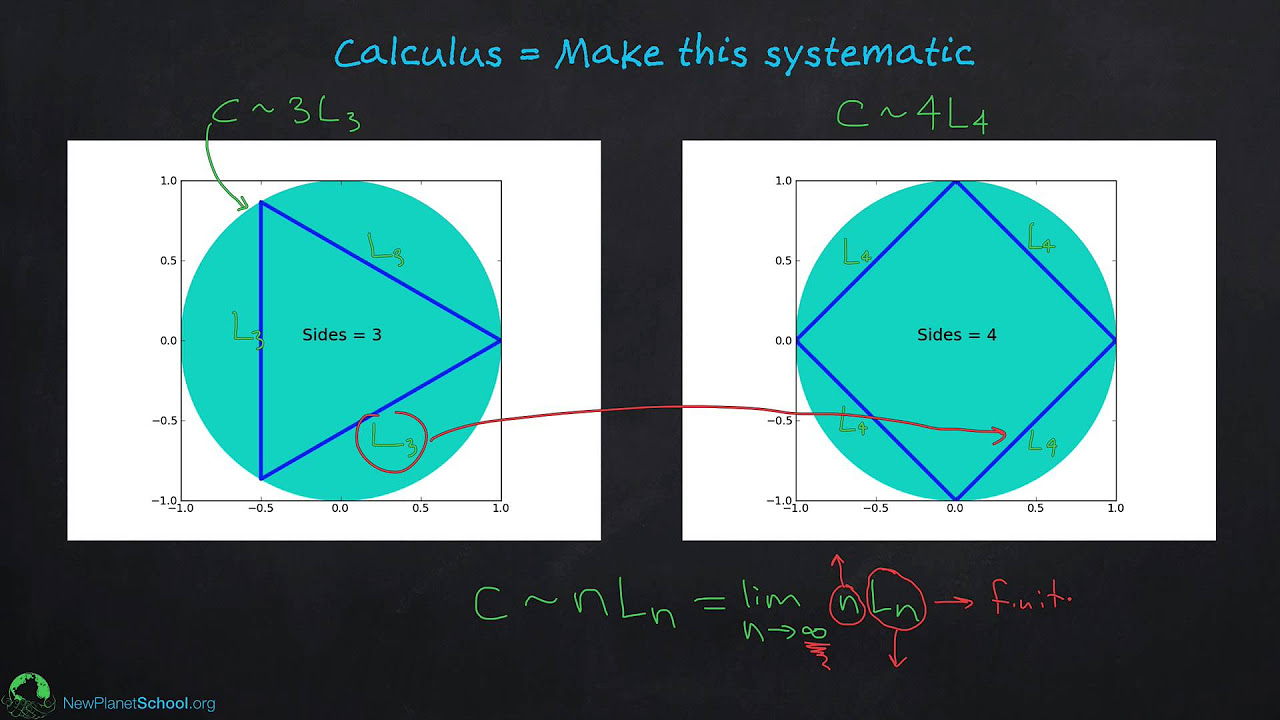
The speaker discusses the dynamic viewpoint that calculus offers, allowing us to analyze static objects as if they were evolving. This approach is used to examine the volume of different structures, such as a cube, by considering them as dynamic entities. The paragraph also touches on the philosophical aspect of calculus, suggesting that it provides not just specific tools like differentiation and integration but also a broader way of interpreting the world. The speaker encourages looking at problems from a calculus perspective to gain new insights. The narrative then shifts to the historical development of calculus, describing it as a conquest of infinity, which is central to understanding the derivative and the integral. The concept of limits and infinite processes are highlighted as key to resolving paradoxes and developing a deeper understanding of calculus.
🔍 The Infinitesimal Nature of Calculus
The focus of this paragraph is on the infinitesimal aspects of calculus, starting with the definition of the derivative, which involves taking the limit as delta t approaches zero. The integral is also discussed as a sum of infinitesimally small pieces, represented by f times dx. The speaker then introduces infinite series as a method for simplifying complex functions into polynomials, which are easier to work with. Examples of functions like the sine function are given to illustrate how they can be represented as infinite polynomials. The concept of exponential functions is also explored, showing how they too can be expressed as infinite series. The paragraph concludes by emphasizing the importance of the limiting process in understanding and applying calculus.
🌟 The Exploration of Infinity in Calculus
This paragraph delves deeper into the concept of infinity in calculus, discussing how it is used in infinite series and the solutions to differential equations. The speaker explains how direction fields can be used to visualize the solutions to differential equations by considering the slope at each point in the plane. The idea of magnifying a graph of a differentiable function to the point where it appears as a straight line is also discussed, highlighting the fundamental principles of calculus. The paragraph then introduces the concept of fractals, which are objects that look the same at every magnification and are not smooth, challenging the traditional ideas of calculus. Examples of fractals, such as the Koch curve and the Devil's Staircase, are given to illustrate these non-smooth, infinitely complex shapes.
🌱 The Ongoing Legacy and Future of Calculus
The final paragraph reflects on the legacy of calculus and its ongoing development. The speaker quotes Isaac Newton, emphasizing the idea that our understanding of calculus is just the beginning of a much larger exploration of knowledge. The paragraph discusses the continuous evolution of calculus, with thousands of papers being written about it and its applications in various fields. The speaker encourages the view that our exploration of calculus is standing on the shoulders of giants, building upon the work of great thinkers like Newton, Leibniz, and Archimedes. The paragraph concludes by celebrating the conceptual development of calculus as a significant milestone in human thought and its continued influence on our understanding of the world.
Mindmap
Keywords
💡Calculus
💡Derivative
💡Integral
💡Optimization
💡Differential Equations
💡Heat Equation
💡Hydrostatic Force
💡Product Design
💡Architectural Structures
💡Infinite Series
💡Fractals
💡Infinity
Highlights
Calculus is a fundamental tool for quantitatively studying change and the combination of parts to form a whole.
Derivative and integral are the two foundational ideas of calculus, motivated by everyday observations.
Calculus is not a static subject; it continues to evolve with ongoing development and application.
The wealth of ideas in calculus is vast, with each concept being just the tip of the iceberg.
The derivative and integral were developed from observing a car's motion on a road.
Calculus is extensively used in understanding the inner workings of a car, such as engine pistons and fuel optimization.
Differential equations, like the heat equation, are used to understand heat dissipation in engines and financial models.
The heat equation has applications beyond heat, such as in financial models like the Black-Scholes model.
Calculus can be applied to various physical concepts and conceptual contexts, including economic and financial issues.
Optimization problems, such as power generation from dams, are ideally suited for calculus.
Calculus aids in determining optimal architectural structures, like the strength of beams cut from a log.
The same optimization techniques used in product design can be applied to rocket science for satellite orbit placement.
The power of abstraction in calculus allows the same techniques to be used across various fields.
Calculus enables a dynamic view of static objects, aiding in analyzing the volume of different structures.
The story of calculus can be seen as the intellectual conquest of infinity, dealing with infinite processes.
The concept of limits is central to calculus, resolving Zeno's paradoxes by understanding infinitesimals.
Infinite series allow for the representation of complex functions as simple polynomials extended to infinity.
Differential equations can be solved using infinite processes to find smooth solutions.
The idea that differentiable functions look like straight lines when magnified is a fundamental aspect of calculus.
The exploration of infinity in calculus led to the discovery of functions that are continuous but nowhere differentiable.
Fractals are mathematical objects that look the same at every magnification and are not smooth like traditional calculus curves.
The Devil's Staircase is an example of a continuous function that is flat almost everywhere yet gets from zero to one.
Calculus is part of an ongoing exploration, with thousands of papers written about it and its extensions.
The study of calculus represents standing on the shoulders of giants, building upon the work of great thinkers.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: