Continuity vs Partial Derivatives vs Differentiability | My Favorite Multivariable Function

Dr. Trefor Bazett
14 Jun 202009:11
EducationalLearning
32 Likes 10 Comments

TLDRThis calculus video explores the complexities of differentiability in multivariable functions, contrasting it with single-variable calculus. It introduces a function that appears discontinuous yet possesses partial derivatives, challenging the conventional rule that discontinuity implies non-differentiability. The script uses this function to illustrate the need for a refined definition of differentiability in higher dimensions, which will be addressed in a subsequent video, sparking curiosity about the forthcoming mathematical concepts.

Takeaways
  • 📚 The script discusses the definition of differentiability in multivariable calculus, highlighting the complexity beyond partial derivatives.
  • 🔍 It emphasizes the importance of continuity and its relationship with partial derivatives in multivariable functions.
  • 🤔 The need for a new concept of differentiability, separate from partial derivatives, is introduced due to the limitations of the single-variable calculus analogy.
  • 📉 The script uses the example of a step function to illustrate the relationship between continuity and differentiability in single-variable calculus.
  • 📈 A multivariable function is introduced that superficially resembles the single-variable step function but behaves differently in higher dimensions.
  • 🚫 The function is shown to be discontinuous at the origin (0,0), as limits along different paths yield different values.
  • 🧐 Despite discontinuity, the script demonstrates that the partial derivatives of the multivariable function exist and are equal to zero.
  • 📌 The existence of partial derivatives does not guarantee continuity, challenging the direct analogy from single-variable calculus.
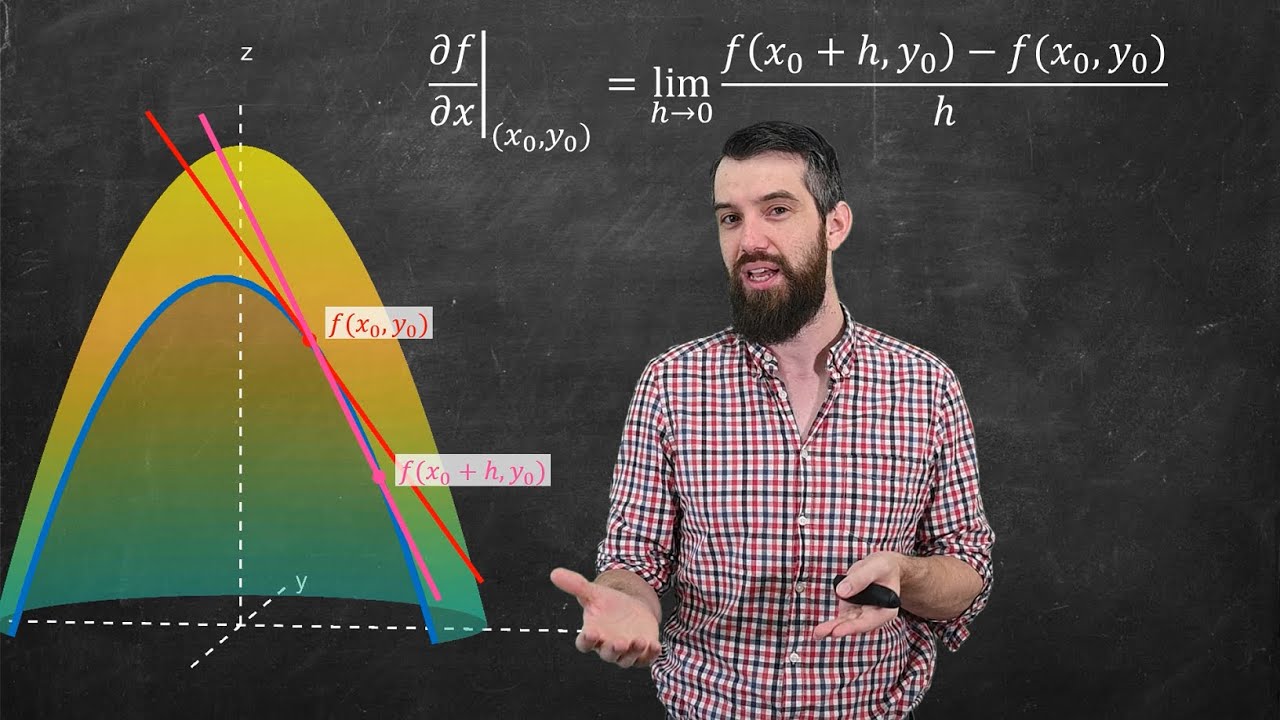
  • 💡 The partial derivative with respect to X is computed, showing that it sees only the constant value of the function along the x-axis.
  • 📏 Similarly, the partial derivative with respect to Y is calculated, revealing the same result of zero due to the function's behavior along the y-axis.
  • 🔑 The script concludes by motivating the need for a refined definition of differentiability in multivariable calculus, which will be addressed in a subsequent video.
Q & A

  • What is the main focus of the video script?

    -The main focus of the video script is to explore the concept of differentiability in multivariable calculus, particularly why partial derivatives alone are not sufficient to define differentiability and the need for a new concept.

  • Why is the relationship between continuity and differentiability in multivariable calculus different from single variable calculus?

    -In single variable calculus, a discontinuous function is not differentiable. However, in multivariable calculus, a function can have partial derivatives and still be discontinuous, as illustrated in the script with a specific example.

  • What is the example used in the script to illustrate the difference between single variable and multivariable calculus?

    -The example used is a function that is zero when either X or Y is not zero and one when X and Y are both zero, which superficially resembles a step function in single variable calculus but behaves differently in multivariable calculus.

  • What property of functions is continuity, and why is it important?

    -Continuity is a property where the limit of a function as it approaches a certain point equals the function's value at that point. It is important because it is a prerequisite for differentiability in single variable calculus and helps in understanding the behavior of functions at specific points.

  • How does the script demonstrate that the given multivariable function is not continuous?

    -The script demonstrates discontinuity by showing that the limit of the function along different paths (e.g., along the x-axis and along the line y=x) yields different values, indicating that the limit does not exist and thus the function is not continuous at the origin.

  • What is the definition of a partial derivative, and how is it computed?

    -A partial derivative is a derivative that measures how a multivariable function changes with respect to one variable while holding the other variables constant. It is computed using the limit definition, where the function is evaluated at points with a small change in the variable of interest as that change approaches zero.

  • Why do the partial derivatives of the given function exist even though the function is discontinuous?

    -The partial derivatives exist because, when considering changes only along the x-axis or y-axis, the function behaves like a constant function (which has a derivative of zero), and thus the partial derivatives along these axes are zero.

  • What does the script suggest we need to define differentiability in multivariable calculus?

    -The script suggests that we need a new concept that goes beyond just having partial derivatives to define differentiability in multivariable calculus, as the relationship between continuity and differentiability is more complex in higher dimensions.

  • What is the significance of the function's behavior along the x-axis and y-axis in determining its partial derivatives?

    -The significance is that the function's behavior along these axes, where it acts as a constant function, allows the partial derivatives to exist and be zero, despite the function being discontinuous at the origin.

  • What does the script imply about the relationship between partial derivatives and the function's value at a point?

    -The script implies that the existence of partial derivatives does not necessarily guarantee that the function is continuous or differentiable at a point, as the function's value and the limit may not be equal.

  • What is the next step proposed in the script to further understand differentiability in multivariable calculus?

    -The next step proposed is to introduce a new concept of differentiability in the subsequent video of the multivariable calculus series, which will provide a more comprehensive understanding of the topic.

Outlines
00:00
📚 Introduction to Multivariable Differentiability

This paragraph introduces the concept of differentiability in multivariable calculus, contrasting it with the simpler notion of partial derivatives. It sets the stage for a deeper exploration by discussing the importance of continuity and the relationship between continuity and partial derivatives. The speaker uses the example of a step function to illustrate the idea that a function must be continuous to be differentiable in single-variable calculus, and then extends this to a multivariable context, highlighting the need for a new concept beyond partial derivatives to fully understand differentiability in higher dimensions.

05:00
🔍 Discontinuity and Partial Derivatives in Multivariable Functions

The second paragraph delves into the complexities of multivariable calculus by examining the partial derivatives of a specific function that is discontinuous at the origin. Despite the function's discontinuity, it is shown that the partial derivatives with respect to both variables exist and are equal to zero. This surprising result challenges the straightforward relationship from single-variable calculus, where discontinuity implies non-differentiability. The paragraph uses visual arguments and limit computations to demonstrate that the function's behavior along different paths can lead to different conclusions about continuity, thus necessitating a more nuanced definition of differentiability in the context of multivariable functions.

Mindmap
Keywords
💡Differentiability
Differentiability in the context of multivariable calculus refers to the ability of a function to have a linear approximation at a given point. It is a key concept that extends the idea of a derivative from single-variable calculus to functions of multiple variables. In the video, differentiability is explored as a property that may not be fully captured by the existence of partial derivatives alone, as illustrated by the function that is discontinuous but has partial derivatives.
💡Partial Derivatives
Partial derivatives are the rate at which a multivariable function changes with respect to one variable, while holding the other variables constant. They are analogous to derivatives in single-variable calculus but operate in higher dimensions. The video uses partial derivatives to examine the function's behavior along different axes, revealing that even though the function is not continuous, it has partial derivatives that are zero.
💡Continuity
Continuity in calculus is a property of a function that guarantees that the function's limit exists at a point and is equal to the function's value at that point. The video discusses continuity as a prerequisite for differentiability in single-variable calculus and contrasts it with the multivariable case, where a function can have partial derivatives but not be continuous.
💡Discontinuity
Discontinuity occurs when a function is not defined at a certain point or when the limit of the function as it approaches a point is not equal to the function's value at that point. The video script uses the example of a step function to illustrate discontinuity and explores how it differs in multivariable functions, where discontinuity does not necessarily imply the absence of partial derivatives.
💡Limit
In calculus, a limit is the value that a function or sequence approaches as the input or index approaches some value. The concept of limits is central to defining continuity and differentiability. The video discusses limits in the context of multivariable functions, showing that different paths to a point can yield different limit values, indicating discontinuity.
💡Multivariable Function
A multivariable function is a function that depends on several independent variables. The video script delves into the complexities of differentiability for such functions, contrasting them with single-variable functions and highlighting the need for a refined definition of differentiability beyond partial derivatives.
💡Tangent Line
A tangent line is a straight line that touches a curve at a single point without crossing it. In the context of derivatives, the slope of the tangent line at a point on a curve represents the derivative of the function at that point. The video uses the concept of a tangent line to explain the difficulty of differentiating the step function at the point where it jumps.
💡Secant Line
A secant line is a straight line that intersects a curve at two or more points. It is used to approximate the tangent line and derivative as the points on the curve come closer together. The video script describes how the secant line between two points on a horizontal line has a slope of zero, which is used to explain the partial derivatives of the given function.
💡Function Value
The function value is the result produced by a function for a particular input or set of inputs. In the context of continuity and differentiability, the function value at a point is crucial. The video script discusses how the function value at a point must equal the limit of the function as it approaches that point for the function to be continuous.
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its independent variable. It is a fundamental concept in understanding the behavior of functions, especially in terms of slopes and rates of change. The video script refers to derivatives in the context of single-variable calculus and contrasts this with the more complex scenario of multivariable functions.
💡Higher-Dimensional Analog
A higher-dimensional analog is a concept or function that extends to multiple dimensions from a concept originally defined in fewer dimensions. In the video, the script discusses how the properties of single-variable functions, such as continuity and differentiability, do not directly translate to multivariable functions, necessitating new concepts and definitions.
Highlights

Differentiability in multivariable functions requires more than just partial derivatives.

A function being differentiable in single-variable calculus implies continuity.

In single-variable calculus, if a function is discontinuous, it is not differentiable.

Example of a step function in single-variable calculus showing discontinuity and non-differentiability.

Multivariable analog of the step function looks like a cross above the axes where x = 0 or y = 0.

Continuity means the limit exists and equals the function value.

Evaluating limits along different paths can show whether a function is continuous.

Example of evaluating the limit along the x-axis (y = 0) for the multivariable step function.

Different paths can yield different limit values, indicating discontinuity.

Partial derivatives can exist even if the function is not continuous.

Definition of partial derivatives involves taking limits while keeping one variable fixed.

Partial derivatives with respect to x and y both exist and are equal to 0 at the point (0,0) for the example function.

Visual interpretation of partial derivatives as slopes of secant lines between points.

The example illustrates that discontinuity does not preclude the existence of partial derivatives.

A new, more robust notion of differentiability is needed for multivariable functions.

Transcripts

Browse More Related Video

What is differentiability for multivariable functions??

BusCalc 16 Continuity and Differentiability

AP Calculus AB: Lesson 2.5 Differentiability

Continuity and Differentiability

Calculus 3: Tangent Planes and Linear Approximation (Video #14) | Math with Professor V

Calculus 1 Lecture 2.1: Introduction to the Derivative of a Function

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Multivariable CalculusDifferentiabilityPartial DerivativesContinuityLimit ConceptsFunction AnalysisHigher DimensionsMath EducationEducational VideoMath ConceptsCalculus 3