College Physics 1: Lecture 17 - Weight, Apparent Weight, and Normal Force
TLDRThis lecture from 'College Physics 1' explores the concepts of weight, apparent weight, and normal force. It clarifies the difference between mass and weight, with mass being a measure of inertia and weight being the gravitational force exerted on an object, measured in newtons. The lecture delves into the relationship between weight and mass, apparent weight during acceleration, and the sensation of weightlessness during free fall. It also covers the normal force, which is the force exerted by a surface in response to pressure, and provides examples to illustrate these concepts, including the behavior of forces in an elevator and on an inclined plane.
Takeaways
- 📚 The lecture introduces the concepts of weight, apparent weight, and normal force within the context of physics.
- 🔍 It clarifies that mass and weight are not the same; mass is a measure of inertia and is scalar, while weight is the gravitational force exerted on an object and is a vector.
- 🌍 The difference between mass and weight is illustrated by considering how an object's weight changes on different planets due to varying gravitational forces.
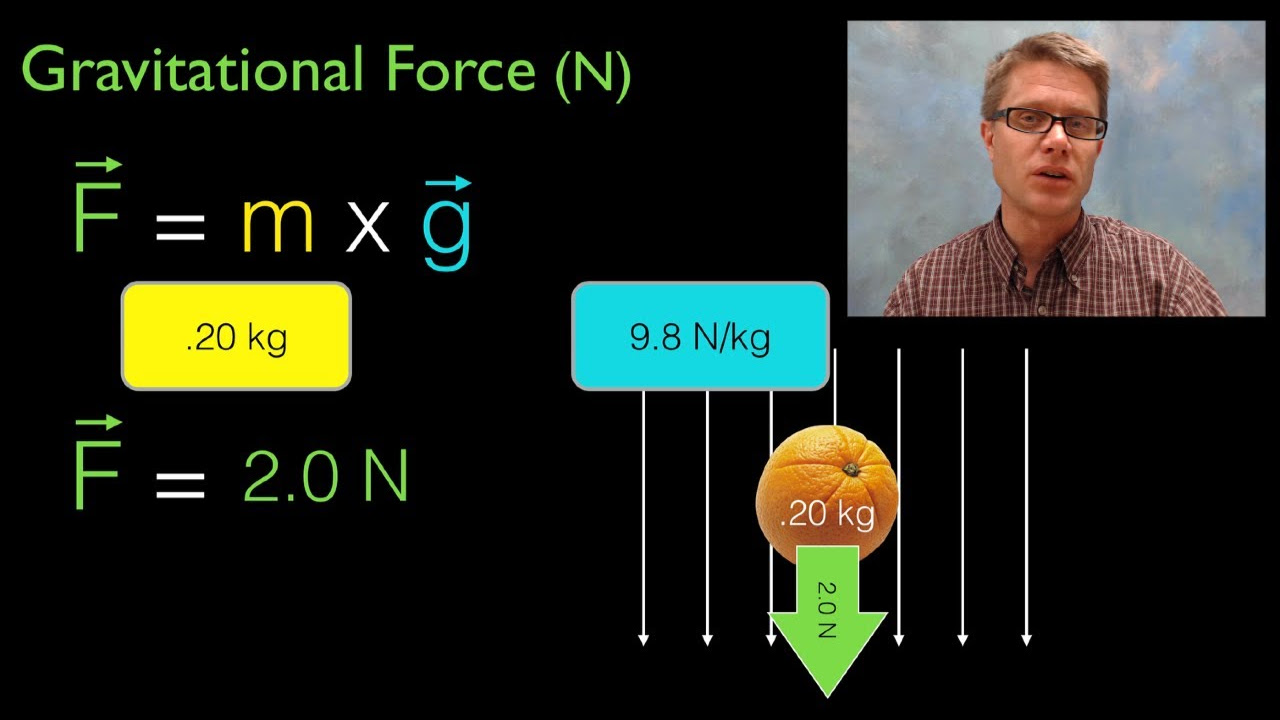
- 🧭 Weight is calculated as the product of an object's mass and the acceleration due to gravity (weight = mass * gravity).
- 🚀 Apparent weight is the force that an object feels due to contact forces, which can differ from actual weight during acceleration, such as in a roller coaster or an elevator.
- 📉 In situations of equilibrium, such as when at rest or moving at a constant speed, the apparent weight equals the actual weight.
- 📈 The sensation of weightlessness occurs when there is no support force acting on an object, as in free fall, even though gravity still acts on the object.
- 🤔 The lecture uses an elevator scenario to explain how the normal force and apparent weight change with the elevator's acceleration.
- 📐 Normal force is always perpendicular to the surface an object is on and adjusts to balance the force exerted on the surface.
- 📚 The lecture concludes with an example problem involving a skier on a slope to demonstrate the application of Newton's second law and the calculation of acceleration.
- 🔑 Key equations introduced include the relationship between weight and mass (weight = mass * gravity) and the acceleration of an object on an incline (acceleration = gravity * sine of the incline angle).
Q & A
What are the key differences between mass and weight?
-Mass is a scalar quantity measured in kilograms that describes an object's inertia, or its resistance to acceleration. Weight, on the other hand, is a vector force measured in newtons and represents the gravitational force exerted on an object by a planet or other massive body. While mass remains constant regardless of location, weight varies depending on the gravitational pull of the environment.
How is weight related to mass and the acceleration due to gravity?
-Weight is directly proportional to mass and the acceleration due to gravity. The relationship can be expressed by the equation: weight (W) equals mass (m) times the acceleration due to gravity (g), or W = m * g. On Earth, g is approximately 9.8 m/s².
Why do astronauts appear to 'bob' around on the surface of the Moon?
-Astronauts on the Moon exhibit a 'bobbing' motion because the Moon's gravity is much lower than Earth's. This reduced gravitational influence results in a lower weight, making it easier for astronauts to move around, which gives the appearance of bobbing.
What is the concept of apparent weight, and how does it differ from actual weight?
-Apparent weight is the weight that an individual feels, which is the magnitude of supporting contact forces, such as the normal force from a surface. It differs from actual weight in that apparent weight can change based on the acceleration experienced by the individual. For example, during a roller coaster ride or in an accelerating elevator, one might feel heavier or lighter than their actual weight due to changes in acceleration.
How can the normal force be described in terms of an object's interaction with a surface?
-The normal force is the force exerted by a surface that is always perpendicular to the surface and equal in magnitude and opposite in direction to the force pressing down on it. It adjusts in strength depending on the force applied to the surface, ensuring that the object remains in contact with the surface.
What happens to a person's apparent weight when they are in an elevator accelerating upwards?
-When an elevator accelerates upwards, a person's apparent weight increases. This is because the normal force, which is what the person feels as their weight, must be greater than the actual weight to provide the necessary upward force to accelerate the person along with the elevator.
How can you determine if an elevator is moving upward or downward based on the scale reading and the person's actual weight?
-If the scale reading (apparent weight) is greater than the actual weight, it indicates that the normal force is greater than the weight, suggesting an upward net force and therefore an upward acceleration. Since the elevator is slowing down, the direction of motion must be opposite to the direction of acceleration, indicating that the elevator is moving downward.
What is the experience of weightlessness, and how can it be achieved?
-Weightlessness is the sensation of having no weight, which occurs when there is no normal force acting on a person, such as when they are in free fall. It can be experienced during activities like skydiving, on roller coasters, or in special aircraft that perform parabolic flight paths to simulate zero-gravity conditions.
How does the normal force change when an object is on an inclined surface?
-On an inclined surface, the normal force remains perpendicular to the surface, but its direction is adjusted relative to the object's tilted axes. The angle between the normal force and the object's weight vector is the same as the angle of the incline, requiring the use of trigonometric functions to calculate the components of the weight acting along and perpendicular to the surface.
What is the acceleration of a skier sliding down a slope, and how can it be calculated?
-The acceleration of a skier sliding down a slope can be calculated using Newton's second law, taking into account the components of the skier's weight along the slope (using sine of the angle of the slope) and the normal force perpendicular to the slope (using cosine of the angle). The acceleration along the slope is given by a = g * sine(theta), where g is the acceleration due to gravity and theta is the angle of the slope.
Outlines
📚 Introduction to Weight and Apparent Weight
This paragraph introduces the concepts of weight and apparent weight, emphasizing the distinction between mass and weight. Mass, measured in kilograms, is defined as a scalar quantity that describes an object's inertia or resistance to acceleration. Weight, on the other hand, is a vector force measured in newtons, representing the gravitational pull exerted by a massive body like Earth. The paragraph also explains how an object's weight can vary depending on the gravitational force of different planets, using the example of an astronaut's experience on the Moon to illustrate the concept of weightlessness. The relationship between mass and weight is established through Newton's second law, highlighting that weight (W) is the product of mass (m) and the acceleration due to gravity (g).
🔍 The Concept of Apparent Weight
The second paragraph delves into the idea of apparent weight, which is the weight that an individual feels due to contact forces. It explains that we do not directly sense gravity but rather the contact forces that support us, such as the normal force from a chair or the floor. The concept is further explored through the example of a roller coaster, where passengers may feel lighter or heavier than their actual weight due to the accelerations experienced. The paragraph also uses the example of an elevator to illustrate how apparent weight changes with acceleration, and introduces the formula for apparent weight (W_apparent = W_true + ma), where 'm' is mass, 'a' is acceleration, and 'W_true' is the true weight of the object.
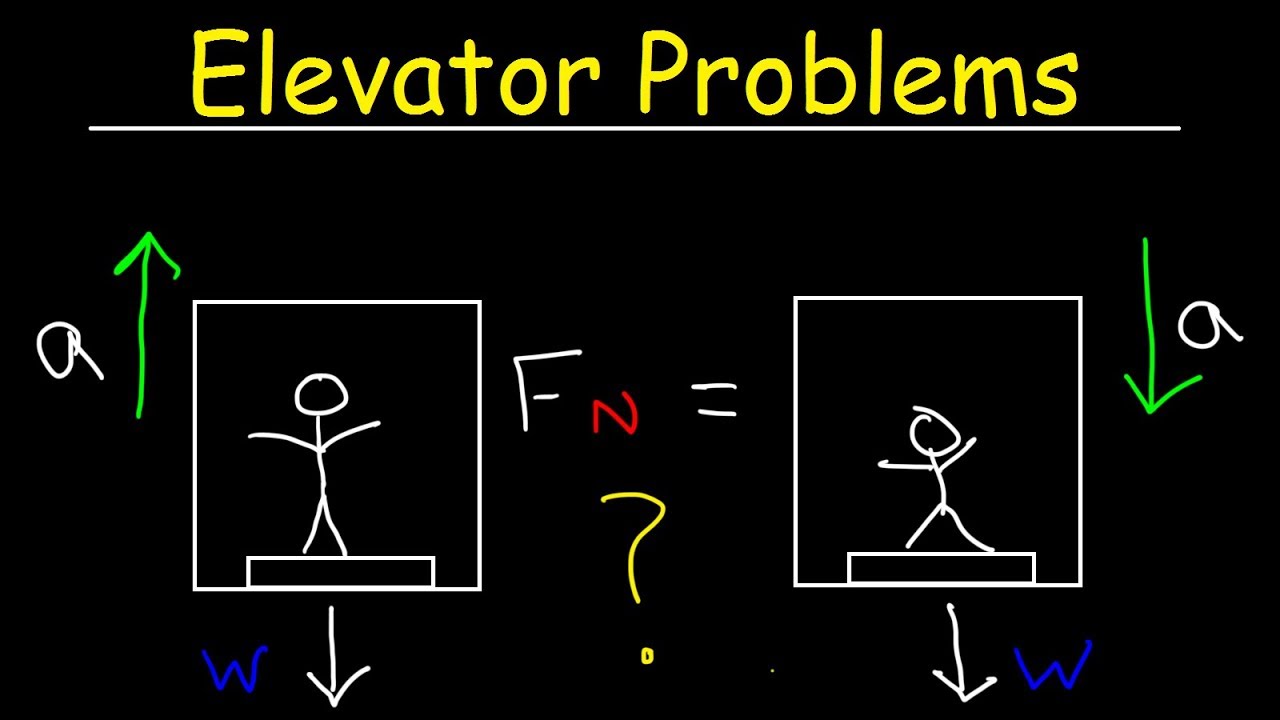
📉 Apparent Weight in Elevator Scenarios
This paragraph presents a scenario involving a person named Anje in an elevator to discuss the concept of apparent weight in more detail. It describes how the scale in the elevator would read 750 newtons as the elevator slows to a stop, indicating Anje's apparent weight. The paragraph uses this example to explain the difference between actual weight and apparent weight, and how the latter can be greater than the former due to the normal force being larger than the gravitational force acting on the person. The explanation involves a free body diagram and Newton's laws, leading to the conclusion that the elevator must have been moving downward when the scale reading was taken.
🚀 Understanding Free Fall and Weightlessness
The fourth paragraph discusses the experience of free fall and weightlessness. It explains that when there is no support, such as in a free-falling elevator, individuals do not feel their weight due to the absence of a normal force. The paragraph clarifies that weightlessness does not mean the absence of weight; rather, it is the lack of a supporting force that results in the sensation of weightlessness. It also mentions a plane that can simulate the experience of weightlessness by performing a maneuver that causes passengers to feel as if they are floating in space.
🛑 The Normal Force and Its Interaction with Surfaces
This paragraph introduces the normal force, which is the force exerted by a surface that is perpendicular to the object in contact with it. It explains that the normal force adjusts to balance the force applied to the surface, increasing in strength as the applied force increases. The paragraph also discusses the importance of considering the normal force when dealing with inclined surfaces, as it requires the use of trigonometry to resolve the weight vector into components parallel and perpendicular to the surface. An example of a skier sliding down a slope is used to illustrate how to calculate the skier's acceleration using Newton's second law and the components of the weight vector.
📐 Newton's Laws and the Skier's Acceleration
The sixth paragraph continues the discussion on the skier's acceleration, focusing on the application of Newton's second law in the context of inclined surfaces. It describes how to set up the problem by drawing a free body diagram and resolving the weight vector into its components along and perpendicular to the slope. The paragraph explains that the skier's acceleration is due to the component of the weight acting parallel to the slope and that the acceleration can be calculated by canceling out the mass from the equation involving the normal force, weight, and acceleration. The example concludes with the calculation of the skier's acceleration as 4.4 meters per second squared.
🚶♂️ Apparent Weight in Elevator Motion
The seventh paragraph presents a series of questions related to apparent weight in the context of elevator motion. It explains that when an elevator accelerates upward, the normal force, and thus the apparent weight, is greater than the actual weight. Conversely, when an elevator is in free fall, there is no normal force, and the apparent weight is zero, resulting in a sensation of weightlessness. The paragraph emphasizes the importance of understanding the relationship between acceleration, the normal force, and apparent weight, and how these concepts apply to different scenarios, such as a box in an accelerating elevator or a person in an elevator with a broken cable.
🏗️ Conclusion and Future Topics
The final paragraph concludes the lecture by summarizing the key points discussed, including the concepts of weight, apparent weight, and the normal force. It also mentions that future lectures will cover other forces such as friction and drag. The paragraph ends with a note of thanks to the viewers for watching and a wish for a great day, highlighting the educational nature of the content and the intention to continue exploring physics concepts in subsequent sessions.
Mindmap
Keywords
💡Weight
💡Mass
💡Free Body Diagram
💡Equilibrium
💡Apparent Weight
💡Normal Force
💡Acceleration
💡Free Fall
💡Incline
💡Newton's Second Law
Highlights
Lecture 17 focuses on the concepts of weight, apparent weight, and normal force.
Mass and weight are distinct; mass is a scalar measured in kilograms and weight is a vector force measured in newtons.
Weight is the gravitational force exerted by a planet or massive object and is direction-dependent.
The relationship between weight (W) and mass (m) is given by W = m * g, where g is the acceleration due to gravity.
Apparent weight is the weight felt by an individual and is influenced by contact forces.
Gravity cannot be felt directly; the sensation of weight comes from contact forces like the normal force.
In situations of equilibrium, apparent weight equals actual weight.
During acceleration, apparent weight can differ from actual weight, as experienced on a roller coaster or in an elevator.
The normal force is always perpendicular to the surface and adjusts to balance the force applied to it.
When an object is in free fall, it experiences weightlessness due to the lack of supporting contact forces.
Free body diagrams are essential for visualizing forces acting on an object and setting up Newton's laws.
On an incline, the normal force and weight vector components must be considered using trigonometric functions.
Example problem: Determining the skier's acceleration down a slope involves using Newton's second law and trigonometry.
The skier's acceleration formula ax = g * sine(theta) is derived and related to motion on a ramp problems.
In an elevator accelerating upward, the normal force on an object is greater than the object's weight.
When an elevator cable breaks and the elevator is in free fall, the scale would read zero newtons due to the sensation of weightlessness.
The lecture concludes with a discussion on the importance of understanding weight, apparent weight, and normal force in various contexts.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: