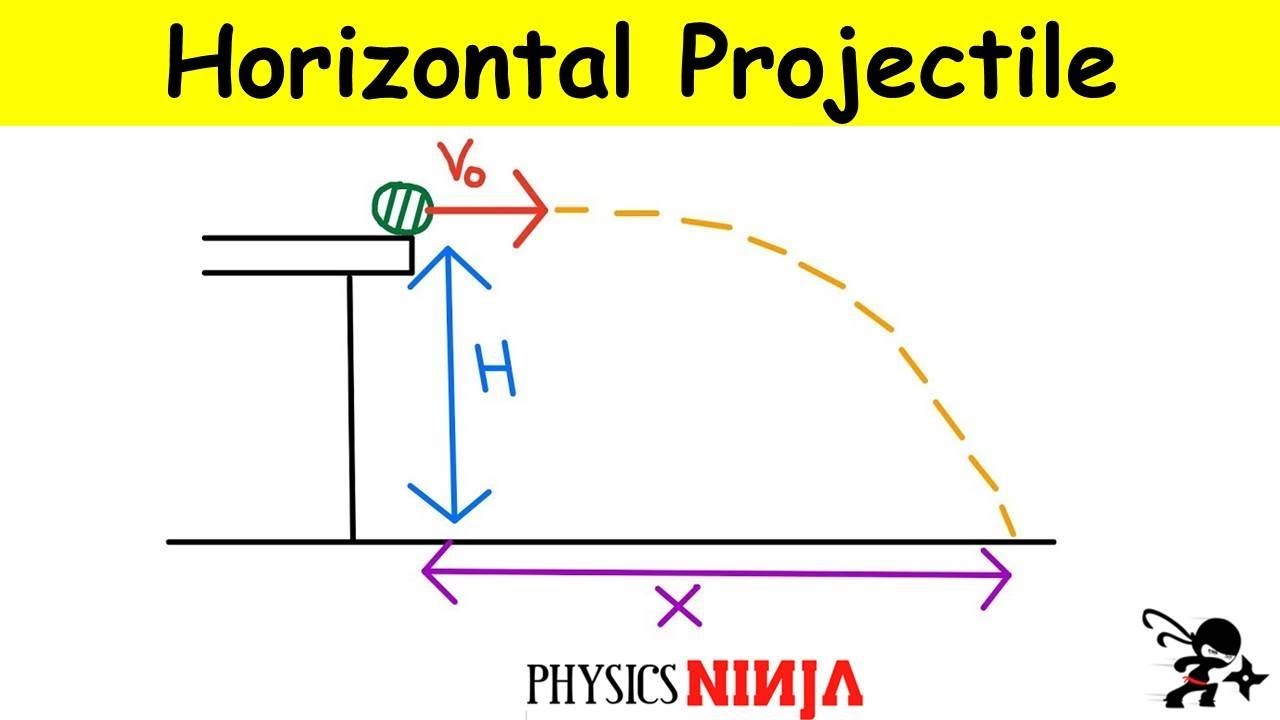
Vertical Projectile Motion: Introduction and Terminology

This paragraph introduces the concept of vertical projectile motion, emphasizing the definitions of 'projectile' and 'free fall'. A projectile is defined as an object that is launched and moves solely under the influence of gravity. Free fall is described as the motion of an object where gravity is the only force acting upon it. The concept of gravitational acceleration is introduced, stating that objects affected only by gravity fall at 9.8 meters per second squared downwards. The paragraph also discusses the assumption of ignoring air resistance in these calculations, which is based on the premise that resistance is proportional to velocity and affected by the object's area.

This section delves into the characteristics of objects in free fall. It explains that all objects in free fall will experience the same acceleration, regardless of their mass or size, which is the gravitational acceleration of 9.8 meters per second squared downwards. The concept of time symmetry is introduced, highlighting that the time taken to reach the maximum height is equal to the time taken to return to the initial position. The paragraph also discusses the principle that the magnitude of velocity at the same point during upward and downward motion will be equal, although their directions will differ.

This paragraph focuses on the behavior of an object's velocity when launched vertically. It explains that at the maximum height, the object's velocity is zero, and the motion exhibits time symmetry, meaning the time taken to ascend to the maximum height is equal to the time taken to descend back to the initial position. The concept of magnitude of velocity is reiterated, emphasizing that while the magnitudes of velocity at the same point during upward and downward motion are equal, their directions are opposite. The paragraph also introduces the idea of vector quantities and how they relate to velocity, with positive and negative values depending on the chosen reference direction.

This section revisits the equations of motion previously learned in grade 10 but adapts them for vertical projectile motion. The equations VF = vi + aΔt, VF^2 = vi^2 + 2aΔy, Δy = viΔt + 0.5Δt^2, and Δy = (vi + vf)/2 × Δt are presented, with the reminder that 'a' represents gravitational acceleration (9.8 m/s^2) which always acts downwards. The paragraph clarifies that while the equations remain the same, the context has shifted from horizontal (grade 10) to vertical motion (grade 12), changing the variable from Δx to Δy. It also mentions that these are vector calculations and that vector concepts will be further explored in subsequent videos.

The paragraph concludes the discussion on vertical projectile motion and sets the stage for future lessons. It mentions that upcoming exercises and examples will help make sense of the concepts introduced. The video ends with a note that the object in the example did not return to the thrower's hand but passed it and hit the ground at a velocity greater than when it was released, reiterating the principle that the final velocity is greater than the initial due to the acceleration caused by gravity.