Inflection points (graphical) | AP Calculus AB | Khan Academy

Khan Academy
26 Jul 201603:20
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script explains the concept of inflection points in the context of a differentiable function 'g' defined over the interval from -4 to 4. Inflection points are characterized by changes in concavity, where the function transitions from concave up to concave down or vice versa. The script uses a visual approach to identify these points by observing changes in the slope of the function's graph. The speaker describes the behavior of the function's slope, moving from increasing to decreasing and back again, and identifies three visible inflection points on the graph of 'g' within the given interval.

Takeaways
  • 📚 The function g is differentiable over the closed interval from -4 to 4.
  • 📈 The graph of g is provided visually to aid in understanding the concept of inflection points.
  • 🔍 Inflection points are defined as points where the concavity of a curve changes.
  • 📉 A curve can transition from concave upwards to concave downwards or vice versa at an inflection point.
  • 📶 The slope of the curve is a key indicator of concavity, with increasing or decreasing slopes signaling changes in concavity.
  • 🚀 At the start, the curve has a high slope that decreases, indicating a change from steep to less steep.
  • 📊 The slope reaches zero and becomes negative, suggesting a further change in concavity.
  • 📉 The slope decreases and becomes more negative, indicating continued concavity changes.
  • 🔄 There is a transition point where the slope starts to increase again, signaling another potential inflection point.
  • 📈 The slope approaches zero and then begins to decrease, indicating yet another change in concavity.
  • 🔢 The graph of g has at least three visible inflection points over the interval.
  • 👀 The identification of inflection points is based on visual analysis of the graph's slope and concavity changes.
Q & A

  • What is the definition of an inflection point in the context of a graph?

    -An inflection point is a point on a curve at which the concavity changes. It is where the graph transitions from being concave up to concave down or vice versa.

  • How does the slope of a curve relate to its concavity?

    -The concavity of a curve is related to the behavior of its slope. A curve is concave up when the slope is increasing, and concave down when the slope is decreasing.

  • What is the significance of the slope's behavior in identifying inflection points?

    -The slope's behavior is crucial in identifying inflection points because it indicates a change in concavity. Inflection points occur where the slope transitions from increasing to decreasing or decreasing to increasing.

  • What is the closed interval mentioned in the script?

    -The closed interval mentioned in the script is from negative four to four, indicating that the function g is defined over this range, including the endpoints.

  • How does the script describe the initial behavior of the slope of the graph of g?

    -The script describes the initial behavior of the slope as very high and steep, indicating a curve that starts off with a high slope that is decreasing.

  • What happens to the slope of the graph of g as it moves from left to right according to the script?

    -The slope starts off high and decreasing, reaches zero, becomes negative, and then decreases further. It then begins to increase again, becoming less negative, and eventually becomes positive and continues to increase.

  • How many inflection points does the script suggest are visible on the graph of g?

    -The script suggests that there are at least three inflection points visible on the graph of g over the interval.

  • What is the relationship between the concavity and the second derivative of a function?

    -The concavity of a function is directly related to the sign of its second derivative. A positive second derivative indicates concave up, while a negative second derivative indicates concave down.

  • What is the mathematical definition of concavity?

    -Concavity refers to the curvature of a function. A function is concave up if its second derivative is positive over an interval, and concave down if its second derivative is negative over an interval.

  • How can one determine the inflection points of a function algebraically?

    -One can determine the inflection points of a function algebraically by finding where the second derivative changes sign, which indicates a change in concavity.

  • What does the script imply about the function g being differentiable over the given interval?

    -The script implies that the function g has a derivative at every point in the interval from negative four to four, which is a prerequisite for having inflection points.

Outlines
00:00
📈 Understanding Inflection Points

The paragraph begins with a voiceover explaining the concept of inflection points, which are points on a graph where the concavity changes. This is illustrated by describing the transition from concave upwards to concave downwards or vice versa. The speaker also explains this in terms of the slope of the curve increasing or decreasing. The paragraph sets the stage for analyzing the graph of the function g to identify its inflection points.

Mindmap
Keywords
💡Differentiable function
A differentiable function is a function whose derivative exists at all points in its domain. In the context of the video, 'g' is described as a differentiable function defined over a specific interval, which implies that its rate of change (slope) can be calculated at any point within that interval. This is crucial for identifying inflection points, as the derivative provides information about the slope of the function.
💡Closed interval
A closed interval in mathematics is an interval that includes its endpoints. In the video, the interval from negative four to four is mentioned, indicating that the function 'g' is being considered within these two specific boundary points. This interval sets the scope for the analysis of the function's behavior, including the search for inflection points.
💡Graph
The graph of a function is a visual representation of the function's relationship between its inputs and outputs. In the video, the graph of 'g' is used to visually identify inflection points. The graph is a key tool for understanding the function's concavity and slope changes, which are essential for identifying inflection points.
💡Inflection points
An inflection point is a point on a curve at which the concavity changes. It's where the function goes from being concave upwards to concave downwards, or vice versa. In the video, the concept of inflection points is central to the discussion, as the speaker is trying to determine how many such points exist on the graph of 'g'. The identification of these points is based on changes in the function's concavity, which is inferred from the graph's shape.
💡Concavity
Concavity refers to the curvature of a function's graph. A graph is said to be concave up if the curve bends upwards like a U, and concave down if it bends downwards. In the video, the speaker discusses changes in concavity as the function 'g' transitions from one type of curvature to another, which is indicative of an inflection point.
💡Slope
Slope, in the context of a function's graph, refers to the steepness or gradient of the curve at a particular point. It is directly related to the derivative of the function. The video discusses how the slope of the function 'g' changes from increasing to decreasing and vice versa, which is a key indicator of inflection points.
💡Increasing slope
An increasing slope indicates that the steepness of the curve is getting steeper as one moves along the curve. In the video, the speaker describes how the slope of 'g' starts high and decreases, then later increases, which is a significant observation for identifying inflection points where the concavity changes.
💡Decreasing slope
A decreasing slope means that the steepness of the curve is becoming less steep. This is a critical observation in the video, as the speaker notes when the slope of 'g' transitions from decreasing to increasing, which is indicative of an inflection point where the function's concavity changes.
💡Transition point
A transition point is a term used in the video to describe a location on the graph where there is a significant change in behavior, such as a change in concavity or slope. The identification of transition points is essential for determining inflection points, as they mark the spots where the function's curvature changes direction.
💡Zero slope
A zero slope on a graph indicates a horizontal tangent at that point. In the video, the speaker notes moments where the slope of 'g' approaches zero, which can be a clue to an inflection point, especially if the slope changes from positive to negative or vice versa as it passes through zero.
💡Positive slope
A positive slope means that the graph of the function is inclined upwards to the right. In the context of the video, the speaker discusses how the slope of 'g' becomes positive after being negative, which signifies a change in the direction of the curve's incline and could indicate an inflection point.
💡Negative slope
A negative slope indicates that the graph of the function is inclined downwards to the right. The video describes how the slope of 'g' becomes more negative, which corresponds to a steeper descent. Changes from a negative to a positive slope, or vice versa, are key to identifying inflection points.
Highlights

The graph of the differentiable function g is analyzed for inflection points over the closed interval from negative four to four.

Inflection points are defined as the points where the concavity of a function changes.

A graphical representation is used to illustrate the concept of concavity changing from upwards to downwards or vice versa.

The slope of the function is described as initially high and steep, indicating a rapid increase.

The slope is observed to decrease, becoming less positive, which means the curve is becoming flatter.

At a certain point, the slope reaches zero before becoming negative, indicating a change in the direction of the curve.

The slope continues to decrease, becoming more negative, which suggests the curve is becoming steeper in the downward direction.

An inflection point is identified where the slope transitions from increasing to decreasing, marking a change from concave upwards to concave downwards.

Another inflection point is noted where the slope transitions from decreasing to increasing, indicating a change from concave downwards to concave upwards.

The slope is observed to increase, becoming less negative, which signifies a shift from a steeper to a less steep curve.

The slope reaches zero again, indicating a potential change in the rate of change of the function.

After reaching zero, the slope becomes positive, suggesting an upward shift in the curve.

The slope continues to increase, becoming more positive, indicating a steeper upward curve.

The analysis concludes that there are three visible inflection points on the graph of g over the given interval.

The importance of understanding the slope's behavior in relation to concavity is emphasized for identifying inflection points.

Graphical analysis is key to visualizing and identifying the changes in concavity and slope.

The concept of inflection points is crucial for understanding the overall shape and behavior of a function's graph.

The process of identifying inflection points involves observing the changes in the slope and concavity of the function.

Transcripts

Browse More Related Video

Worked example: Inflection points from first derivative | AP Calculus AB | Khan Academy

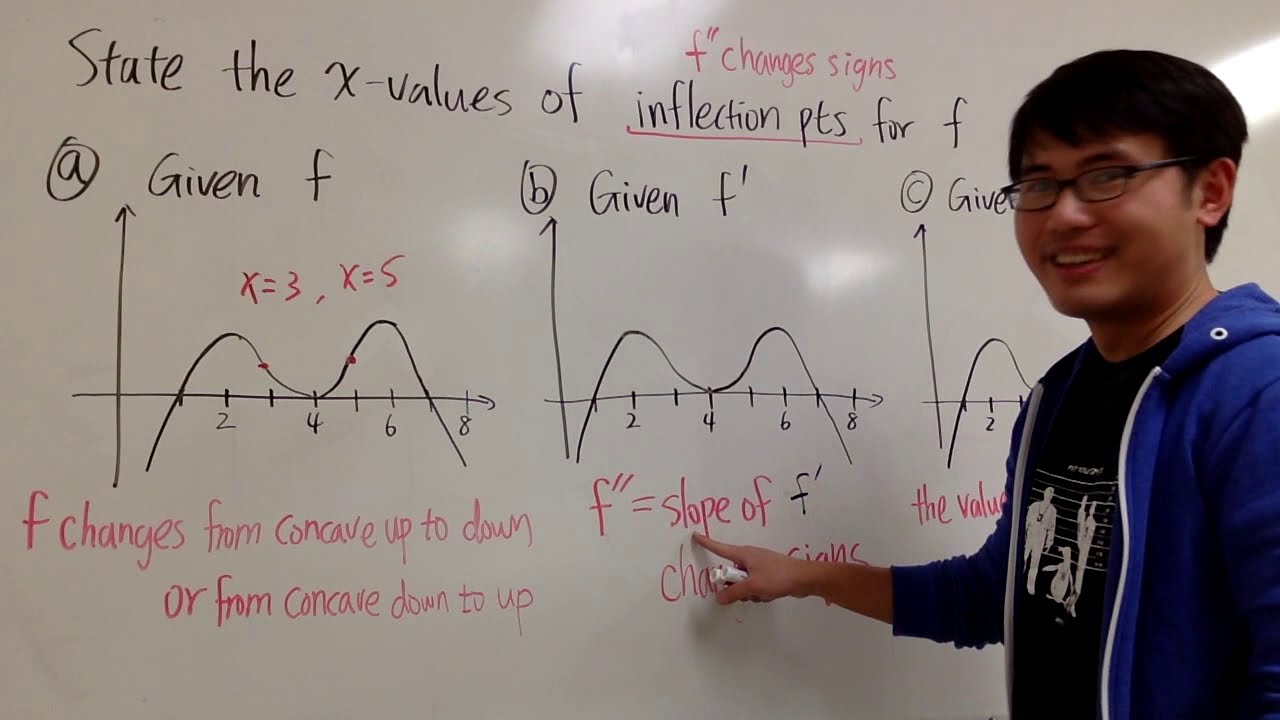
Points of inflection from the graphs of f, f' or f''

What the Second Derivative Tells You about a Graph

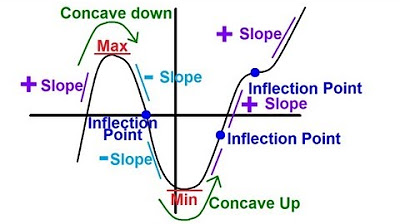
Calculus - Slope, Concavity, Max, Min, and Inflection Point (1 of 4) Trig Function

How to Find Inflection Points

Concavity and the 2nd derivative

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Inflection PointsCalculusGraph AnalysisSlope ChangesConcavityDifferentiableClosed IntervalFunction GraphVisual MathEducational Content