Calculating Sample Size

NREF

9 Sept 201417:56

EducationalLearning

32 Likes 10 Comments

TLDRThe transcript outlines the critical process of calculating sample size for various types of studies, emphasizing the importance of efficiency and resource management. It discusses factors influencing sample size, such as significance level, power, prevalence of factors, and test efficiency. The speaker simplifies complex statistical concepts and provides formulas for calculating sample sizes in different scenarios, including qualitative and quantitative data. The transcript also highlights the significance of confidence intervals and the impact of sample size on study power. Finally, it introduces a software tool, G*Power, to simplify the sample size calculation process.

Takeaways

🔍 The importance of calculating an adequate sample size in a study is to ensure efficiency and avoid wasting resources, as well as to prevent retrospectively realizing that the study was underpowered.
💰 The cost per patient and the total budget are critical factors in determining the sample size, as they directly influence the number of participants that can be included in a study.
📉 Significance level (alpha) is inversely related to sample size; a lower alpha requires a larger sample size to maintain statistical power.
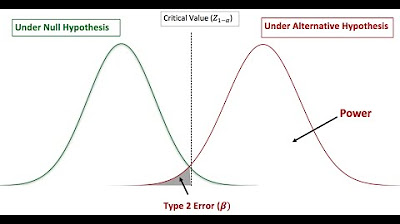
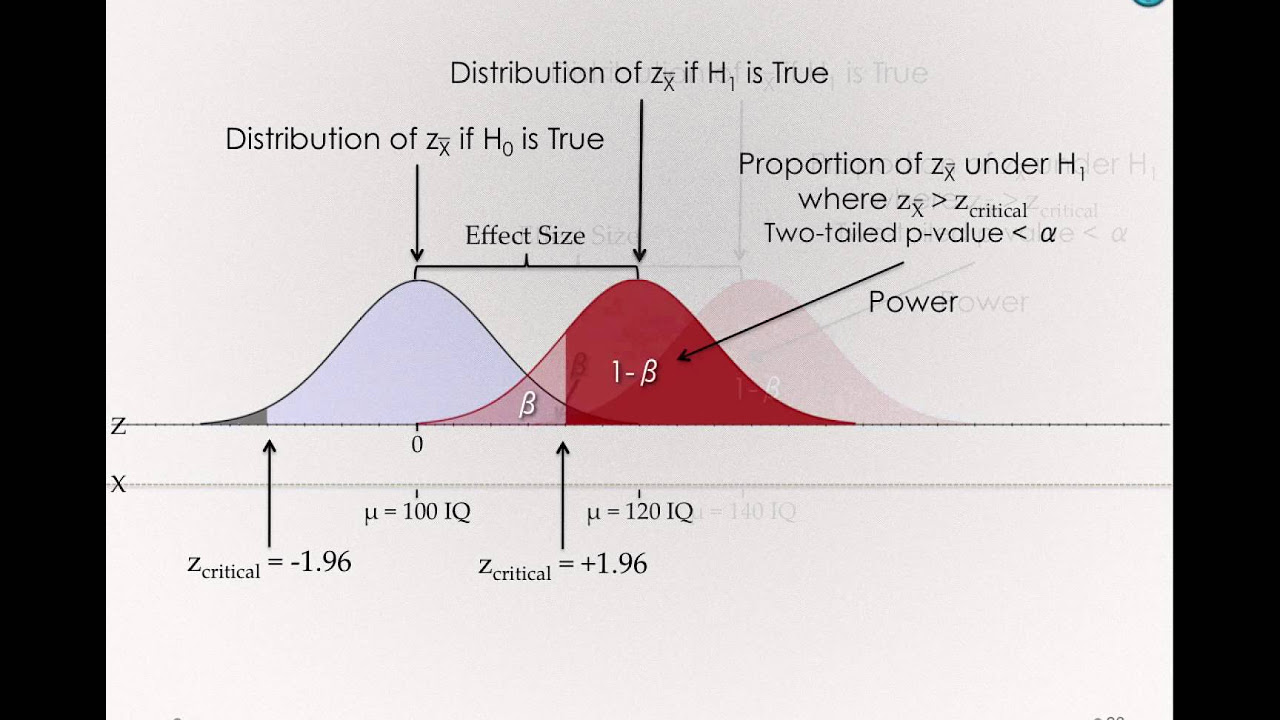
⚖️ Statistical power (1 - beta) is directly related to sample size; increasing power requires a larger number of patients to detect an effect.
📊 The expected prevalence of the factor of interest affects sample size; more common factors require fewer patients, while rarer factors necessitate more patients.
🧬 Test efficiency is crucial; selecting a test that can simplify data and include all necessary variables can reduce the number of samples needed.
📚 Study design is pivotal; considering primary and secondary outcomes, as well as factors like attrition rates and compliance, is essential for accurate sample size calculations.
🔢 The type I error (alpha) and type II error (beta) are key values that dictate the required sample size for a certain power level in a study.
📈 Confidence intervals and their width can impact the perceived significance of results and, by extension, the sample size needed to achieve those results.
📉 The relative risk and its confidence interval are calculated based on the incidence rates in different groups, and a narrower confidence interval indicates a more precise estimate.
🛠️ There are various formulas for calculating sample size depending on the type of data (qualitative or quantitative) and the statistical test being used (e.g., T-test, ANOVA).
💻 Software like G*Power simplifies the process of calculating sample size by allowing users to input specific parameters and obtaining the required sample size without complex calculations.

Q & A

Why is it necessary to calculate the sample size for a study?
-Calculating the sample size is crucial because it helps ensure that the study is efficient and cost-effective. It prevents the waste of resources and the risk of retrospectively realizing that there were not enough participants to draw meaningful conclusions from the study.
What is the relationship between sample size and significance level?
-As the sample size increases, the significance of the results also increases because the findings are more generalizable to the population, reducing random error. Conversely, a higher significance level (smaller alpha) requires a larger sample size to maintain statistical power.
How does the power of a study relate to its sample size?
-The power of a study, which is 1 minus the probability of a Type II error (beta), typically increases with a larger sample size. More patients are usually needed to increase the power of the study and detect an effect if it exists.
What is the impact of the expected prevalence of factors of interest on the sample size?
-If the factor of interest is more common, fewer patients are needed in the study. However, if the factor is rarer, more patients are required to ensure that the study has enough instances of the factor to analyze.
Can you explain the concept of test efficiency in the context of sample size calculation?
-Test efficiency refers to selecting a test that can simplify the data collection process. An efficient test can handle multiple variables or require fewer tests to achieve the necessary sensitivity, thus potentially reducing the number of patient samples needed.
What factors should be considered when calculating the sample size for a study?
-Factors to consider include significance level, power, expected prevalence of factors of interest, test efficiency, study design, primary and secondary outcomes, attrition rate, compliance, and response rates from different populations.
What is the significance of the beta error in the context of sample size calculation?
-Beta error represents the probability of making a Type II error, which is failing to detect an effect when there is one. The power of the study is 1 minus beta, so increasing the power requires a larger sample size to reduce the chance of a beta error.
How does the confidence interval affect the sample size required for a study?
-A smaller confidence interval, which indicates greater precision, requires a larger sample size. As the sample size increases, the confidence interval narrows, increasing the confidence in the study's results.
Can you provide an example of how to calculate the sample size for a study involving two proportions?
-To calculate the sample size for a study involving two proportions, you can use a formula that takes into account the average of the two proportions, the desired difference, and the confidence level. For instance, if you're looking for a 4% difference in the incidence of hypertension between two groups with an average proportion of 0.5, you would calculate the sample size accordingly.
What is G*Power and how can it assist in sample size calculation?
-G*Power is a software tool that simplifies the process of calculating the required sample size for a study. Users can input parameters such as effect size, alpha level, power, and test type to quickly determine the number of samples needed without manually working through mathematical formulas.

Outlines

00:00

🔍 Importance of Sample Size in Research Studies

The speaker discusses the critical role of calculating sample size in various types of studies, such as cohort, case-control, and randomized trials. The aim is to obtain a sample that can effectively represent the larger population, allowing for the testing of hypotheses and generalizable conclusions. The speaker emphasizes the balance between efficiency and resource allocation, highlighting the importance of not underestimating the required sample size to avoid wasting resources. The discussion includes the factors that determine sample size, such as significance level, power, and expected prevalence of factors of interest. The speaker also engages with the audience to explore the relationships between sample size, significance level, and power, using examples to illustrate how these factors influence the number of participants needed in a study.

05:01

📊 Understanding the Impact of Significance Level and Power on Sample Size

This paragraph delves deeper into the relationship between sample size, significance level, and power. The speaker explains that as the sample size increases, so does the significance of the results, making them more generalizable. The discussion contrasts different significance levels (alpha values) and their impact on the required sample size, with higher significance levels necessitating larger samples. The concept of power is also explored, with the speaker clarifying that increasing the power of a study (reducing the chance of a type II error) requires a larger sample size. The speaker uses interactive questioning with the audience to clarify these concepts and their practical implications for study design.

10:03

🧬 Factors Influencing Sample Size Calculation

The speaker continues the discussion by examining additional factors that influence sample size calculation, such as the expected prevalence of factors of interest and test efficiency. It is explained that more common factors require fewer participants, while rarer factors necessitate larger samples. The importance of selecting efficient tests that can simplify data analysis is also highlighted, with examples provided to illustrate the point. The speaker also touches on the importance of study design, considering primary and secondary outcomes, and learning from previous studies to account for factors like attrition rates and compliance. The paragraph concludes with a detailed explanation of how to calculate sample size using a 2x2 table, emphasizing the significance of type I and type II errors in determining sample size.

15:05

📚 Practical Examples and Tools for Sample Size Calculation

In this paragraph, the speaker provides practical examples of how to calculate sample size for different clinical scenarios, considering both qualitative and quantitative data. Four formulas are presented for different scenarios, and the speaker walks through each example, demonstrating how to apply the formulas to calculate the required sample size. The importance of understanding the type of data (qualitative or quantitative) and the analysis method (e.g., one-sided T-test, two-sided T-test, ANOVA) is emphasized. The speaker also introduces a software tool called G*Power, which simplifies the process of calculating sample size by allowing users to input specific parameters and obtain the required sample size for various types of tests. The paragraph concludes with a demonstration of how to use G*Power to streamline the sample size calculation process.

Mindmap

Keywords

💡Population Size

Population size refers to the total number of individuals in a group that is being studied or from which a sample is drawn. In the context of the video, it is crucial for determining the adequate number of subjects needed for a study to ensure the results can be generalized to the larger population. The script mentions that we can't test the whole population, so we aim to obtain a representative sample size to test a hypothesis and draw conclusions.

💡Sample Size

Sample size is the number of subjects or observations included in a study. It is a critical aspect of research design, as it impacts the power of the study and the generalizability of the results. The script emphasizes the importance of calculating an adequate sample size to avoid wasting resources and to ensure the study has enough power to detect meaningful effects.

💡Efficiency

In the context of the video, efficiency pertains to the optimal use of resources such as time, money, and effort in conducting a study. The script discusses the trade-off between the amount of money available for a study and the cost per sample, highlighting the need to avoid retrospectively realizing that not enough participants were involved.

💡Significance Level

The significance level, often denoted by alpha (α), is the probability of rejecting the null hypothesis when it is true. In the script, it is mentioned that as the sample size increases, the significance of the results increases, reducing random error and making the findings more generalizable. A lower significance level (e.g., 0.01) requires a larger sample size to achieve the same level of confidence in the results.

💡Power

Power is the probability that a study will detect an effect if there is one (1 - β, where β is the probability of a type II error). The script explains that increasing the power of a study, such as aiming for 80% or 95%, typically requires a larger sample size to ensure that a true effect can be detected with confidence.

💡Prevalence

Prevalence refers to the proportion of a particular feature or condition in a population. The script mentions that the expected prevalence of factors of interest affects the sample size needed. If a factor is more common, fewer patients are needed in the study, whereas a rarer factor would require a larger sample size.

💡Test Efficiency

Test efficiency refers to the effectiveness and simplicity of a test or measurement tool used in a study. The script uses the example of a pregnancy test being highly sensitive and efficient compared to a more complex gene chip analysis, which may require multiple tests to achieve the same level of sensitivity.

💡Study Design

Study design encompasses the structure and approach of a research study, including the selection of participants, the measurement of variables, and the analysis plan. The script notes that study design is important for calculating sample size, as it involves considering primary and secondary outcomes, as well as factors like attrition rates and response rates.

💡Type I and Type II Errors

Type I error (α) is the incorrect rejection of a true null hypothesis (a 'false positive'), while Type II error (β) is incorrectly failing to reject a false null hypothesis (a 'false negative'). The script explains that increasing the power of a study reduces the chance of a Type II error, and understanding these errors is crucial for determining sample size and interpreting study results.

💡Confidence Interval

A confidence interval provides a range of values within which the true population parameter is likely to fall, with a certain level of confidence. The script illustrates how the width of the confidence interval changes with the sample size, affecting the precision of the study's estimates and the power to detect an effect.

💡Relative Risk

Relative risk is a measure of the risk of an event occurring in an exposed group compared to an unexposed group. In the script, the calculation of relative risk is demonstrated using a 2x2 table, showing how the risk of an event is 1.5 times higher in one group compared to another, which is a key metric in understanding the impact of a particular exposure or intervention.

Highlights

The importance of calculating an adequate sample size in a study to ensure efficiency and avoid wasting resources.

The concept that larger sample sizes increase the generalizability of results and reduce random error.

The relationship between significance level and sample size, where a higher significance level requires a larger sample size.

The impact of study power on sample size, with higher power typically necessitating more patients in the study.

The consideration of expected prevalence of factors of interest in determining the number of patients needed.

The role of test efficiency in sample size determination, with more efficient tests potentially requiring fewer samples.

The significance of study design, including primary and secondary outcomes, in calculating sample size.

The importance of considering attrition rates and compliance in the planning phase of a study.

The use of the 2x2 table and statistical concepts like type one and type two errors in sample size calculations.

The impact of confidence intervals on power and sample size, with narrower intervals indicating higher confidence.

Different formulas for calculating sample size based on the type of data (qualitative or quantitative).

The example of using Z-scores to determine sample size for different confidence levels.

The application of ANOVA for calculating sample size in studies comparing the effects of two drugs.

The calculation of sample size for detecting a specific difference in proportions between two groups.

The use of software like G*Power to simplify the process of calculating sample sizes for various types of studies.

The necessity of understanding the type of variable (qualitative or quantitative) before starting the sample size calculation.

The practical application of sample size calculation in clinical scenarios to answer specific research questions.

Transcripts

Browse More Related Video

Power and Sample Size Calculation

Sample Size Calculation Made Easy - Case Control Study Design -HeDaL

Sample Size Justification by Daniel Lakens

Power & Effect Size

Power Analysis and Sample Size Decisions

Factors Affecting Power - Effect size, Variability, Sample Size (Module 1 8 7)