2022 AP Calculus AB Exam FRQ #2
TLDRIn this video, the presenter tackles an area and volume problem from the 2022 Calculus AB exam. They begin by defining functions f(x) and g(x), and identifying their intersection points, including one at x = b, where b is greater than zero. The presenter calculates the area enclosed by the graphs of f and g, finding it to be approximately 3.604 square units. They then determine that the vertical distance between the graphs, represented by h(x), is decreasing at x = -0.5. Next, the video explores the volume of a solid with square cross-sections, which are perpendicular to the x-axis, and calculates this to be approximately 5.340 cubic units. Finally, the presenter addresses the rate of change of the area of a cross-section above a vertical line moving at a constant speed of seven units per second, concluding with a rate of approximately -9.272 square units per second. The video is both informative and well-structured, providing step-by-step solutions to complex calculus problems.
Takeaways
- 📈 The video discusses a problem from the 2022 Calculus AB exam, which is an area and volume problem.
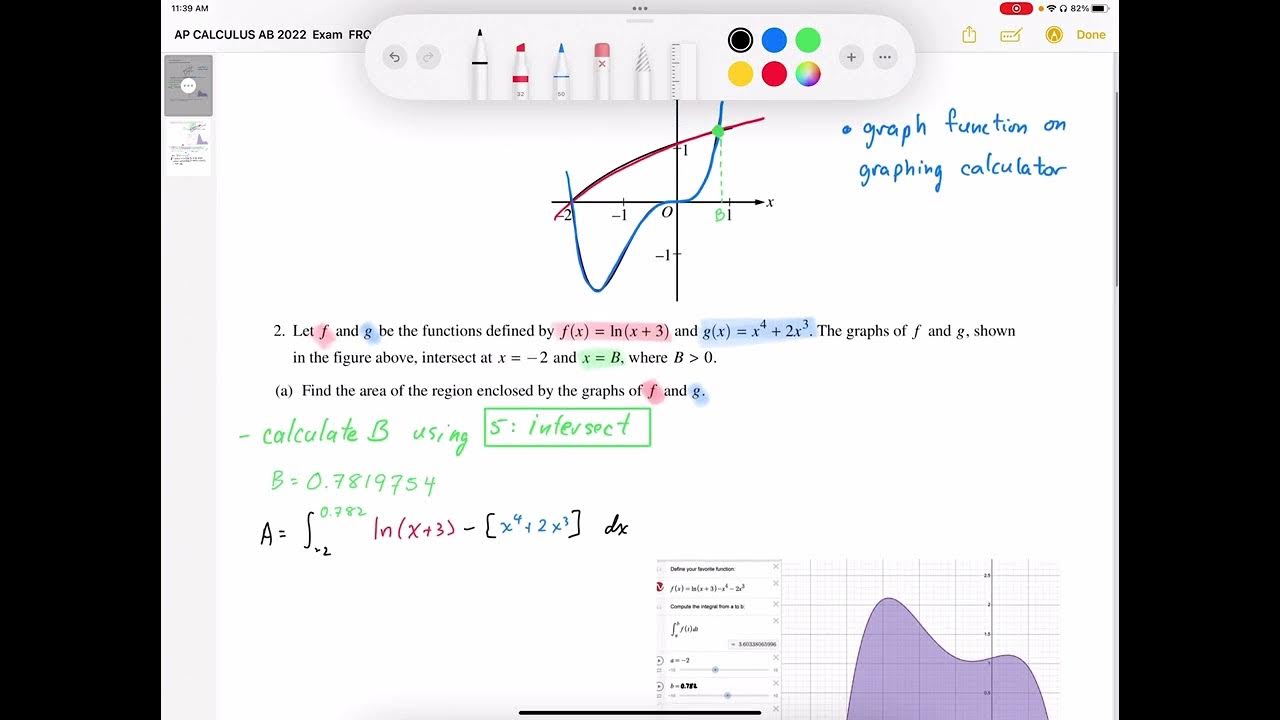
- 🔍 Two functions, f(x) = ln(x) + 3 and g(x) = x^4 + 2x^3, are defined and their graphs intersect at x = -2 and x = b, where b > 0.
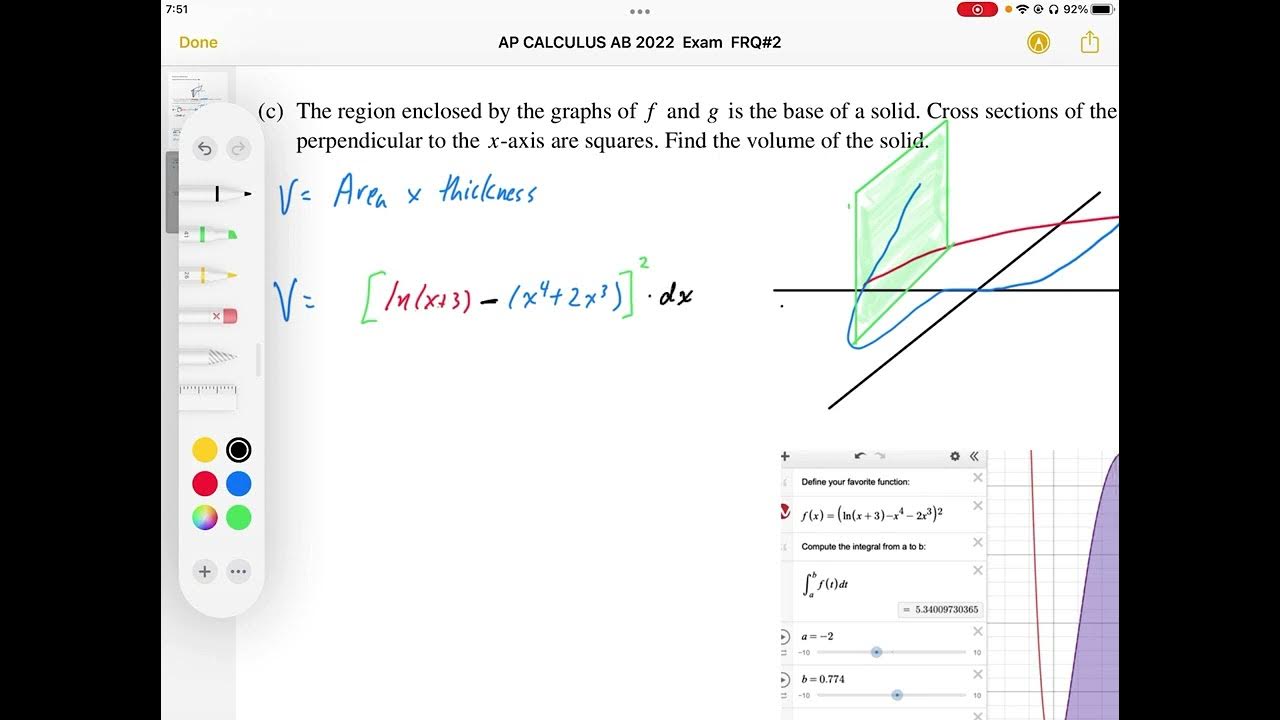
- 🧮 The first task is to find the area enclosed by the graphs of f and g, which is done by calculating the integral from -2 to b of f(x) - g(x).
- 📐 The intersection at x = b is found to be approximately 0.781975, which is used throughout the problem.
- 📊 The area under the curve is calculated to be approximately 3.604 square units using a calculator.
- 📉 The function h(x) represents the vertical distance between the graphs of f and g, and it is determined that h(x) is decreasing at x = -0.5 by finding the derivative h'(x).
- 🔢 The derivative h'(-0.5) is found to be exactly -0.6, indicating a decreasing vertical distance at that point.
- 🟠 The volume of a solid with cross sections that are squares, based on the region between f and g, is calculated by integrating the square of the difference of the functions from -2 to b.
- 🚀 The volume calculation results in approximately 5.340 cubic units, using the stored value of b from the area calculation.
- ⏱ When considering a vertical line moving at a constant rate of seven units per second, the rate of change of the area of the cross section above the line at x = -0.5 is found using the chain rule.
- 📌 The rate of change of the area with respect to time (da/dt) at x = -0.5 is calculated to be approximately -9.272 square units per second.
- 📚 The video concludes with a promise to return for more problems, wishing viewers good luck and hoping they found the explanation helpful.
Q & A
What is the main topic of the video?
-The video is about solving a calculus problem from the 2022 calculus AB exam, which involves finding area, volume, and analyzing the behavior of functions f(x) and g(x).
What are the functions f(x) and g(x) defined as in the video?
-The function f(x) is defined as the natural logarithm of x plus 3, and g(x) is defined as x to the fourth power plus 2x cubed.
At what x-values do the graphs of f and g intersect?
-The graphs of f and g intersect at x equals -2 and at x equals approximately 0.781975, which is stored as b in the calculator.
How is the area enclosed by the graphs of f and g calculated?
-The area is calculated by integrating the top function (f(x)) minus the bottom function (g(x)) from x = -2 to x = b.
What is the approximate area enclosed by the graphs of f and g?
-The approximate area enclosed by the graphs of f and g is 3.604 square units.
How is the derivative of h(x) found in the video?
-The derivative of h(x), denoted as h'(x), is found by calculating the derivative of the difference between the functions f(x) and g(x).
What does the sign of h'(-0.5) indicate about the function h(x) at that point?
-The sign of h'(-0.5) being negative indicates that the function h(x) is decreasing at x equals -0.5.
What is the shape of the cross-sections of the solid formed by the graphs of f and g?
-The cross-sections of the solid are squares, with the side length being the vertical distance between the graphs of f and g.
How is the volume of the solid with known cross-sections calculated?
-The volume is calculated by integrating the square of the difference between f(x) and g(x) from x = -2 to x = b.
What is the approximate volume of the solid with the described cross-sections?
-The approximate volume of the solid is 5.340 cubic units.
What is the rate of change of the area of the cross section above a vertical line moving at a constant rate of seven units per second when the line is at x equals -0.5?
-The rate of change of the area of the cross section with respect to time (da/dt) at x equals -0.5 is approximately negative 9.272 square units per second.
What is the significance of the domain warning when taking the derivative of the natural logarithm function?
-The domain warning signifies that the domain of the derivative function might be different and smaller than the domain of the original function, since the natural logarithm requires its argument to be positive.
Outlines
📈 Calculating Area Between Two Functions
The video begins with an introduction to solving a problem from the 2022 Calculus AB exam, focusing on an area-volume query. The functions f(x) = ln(x) + 3 and g(x) = x^4 + 2x^3 are defined, and their graphs intersect at x = -2 and x = b (where b > 0). The first task is to find the area enclosed by these functions. The presenter graphs the functions, identifies the intersection points, and uses these to calculate the area under the top function f(x) minus the area under the bottom function g(x) between the interval [-2, b]. The integral calculation results in an area of approximately 3.604 square units.
📊 Analyzing the Behavior of a Function
The second part of the video deals with the vertical distance h(x) between the graphs of f and g. The presenter determines whether h(x) is increasing or decreasing at x = -0.5. By calculating the derivative h'(x) and evaluating it at x = -0.5, the presenter finds that h'(-0.5) is negative, indicating that h(x) is decreasing at that point. This conclusion is important for understanding the behavior of the function in question.
Mindmap
Keywords
💡Natural Logarithm
💡Graph Intersection
💡Area Calculation
💡Volume of Solid
💡Derivative
💡Integral
💡Vertical Distance
💡Cross Section
💡Rate of Change
💡Chain Rule
💡Solid of Revolution
Highlights
Introduction to solving an area and volume problem from the 2022 Calc AB exam, focusing on functions f(x) and g(x).
Explanation of the functions f(x) = ln(x) + 3 and g(x) = x^4 + 2x^3, their intersection points, and the use of a graphing calculator to determine these points.
Identification of intersection points at x = -2 and x = b, with b approximated and stored in the calculator for further calculations.
Calculation of the area enclosed by the graphs of f and g, using integration from x = -2 to b of the top function minus the bottom function.
Result of the area calculation approximating to 3.604 using integral computation on a calculator.
Introduction of the function h(x) representing the vertical distance between the graphs of f and g for the interval from -2 to b.
Analysis of whether the function h(x) is increasing or decreasing at x = -0.5 using derivative h'(x) calculated via calculator.
Determination that h'(x) at x = -0.5 is negative, indicating that the vertical distance is decreasing.
Introduction to the concept of a solid with cross-sections perpendicular to the x-axis, where each cross-section is a square, to calculate volume.
Explanation of computing volume by integrating the area of square cross-sections along the x-axis from -2 to b.
Result of volume calculation approximating to 5.340, with emphasis on consistency in decimal precision.
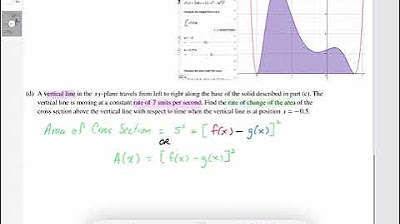
Scenario setup where a vertical line travels left to right through the region, impacting calculations related to the movement rate and area changes.
Explanation of how the movement of the vertical line (dx/dt = 7) affects the rate of change of the area of the cross-section at a specific point.
Use of the chain rule to find the rate of change of the area with respect to time, calculating dA/dt.
Final calculation of dA/dt at x = -0.5, yielding a result of approximately -9.272, indicating the rate at which the cross-sectional area is changing as the line moves.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: