2022 AP Calculus AB Free Response #2
TLDRThe video script is a detailed walkthrough of a calculus problem involving the functions f(x) = ln(x + 3) and g(x) = x^4 + 2x^3. The presenter guides viewers through finding the area enclosed by the graphs of these functions, identifying the bounds of integration by plotting the intersection points of the functions. They then calculate the area using the integral of f(x) - g(x) from -2 to 0.78, resulting in an area of 3.604 square units. The presenter also explores whether the vertical distance between the graphs, h(x), is increasing or decreasing by finding its derivative at a specific point, concluding that it is decreasing. Finally, the video addresses the volume of the solid formed by the cross-section of the graphs and the rate of change of the cross-sectional area with respect to time as a vertical line moves along the base of the solid at a constant rate. The presenter uses the derivative to find the rate of change of the area, resulting in a value of -9.272 square units per second.
Takeaways
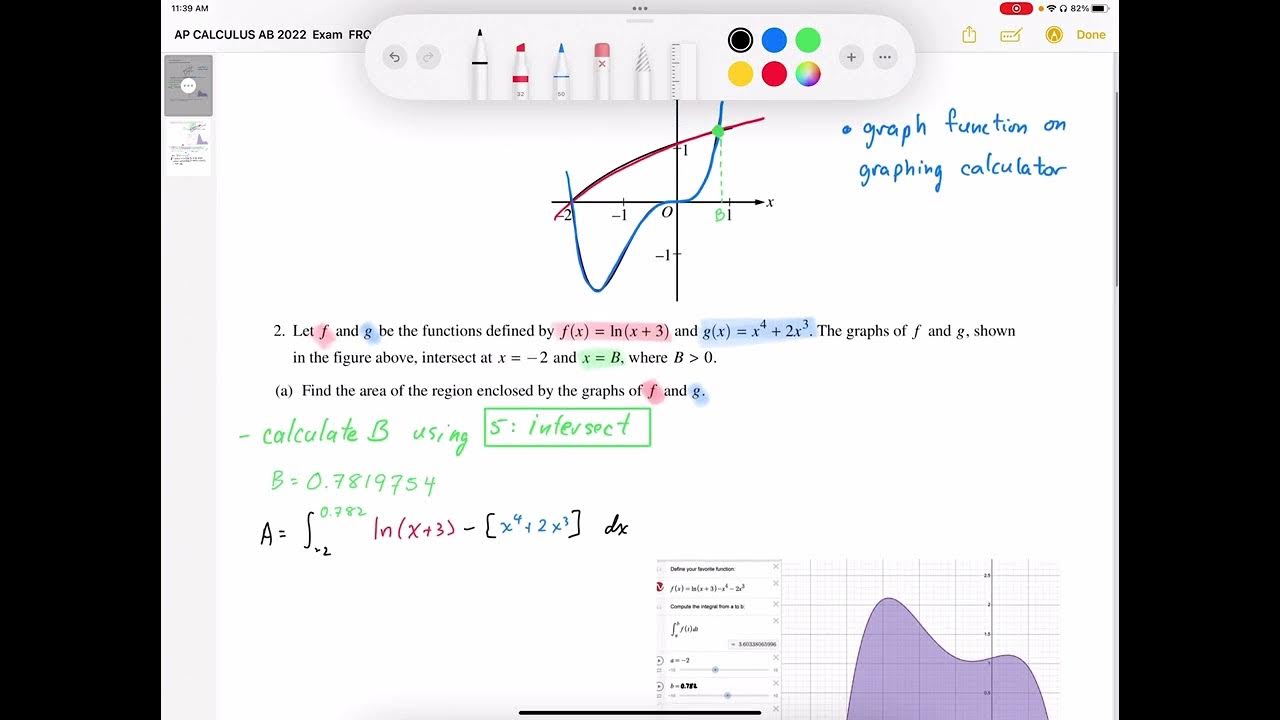
- 📊 The problem involves finding the area enclosed by two functions, f(x) and g(x), and their graphs are provided for reference.
- 🧮 The area is calculated by integrating the difference between the functions, f(x) - g(x), over the bounds where they intersect.
- 📌 The bounds of integration are determined by setting f(x) equal to g(x) and solving for x, which gives the intersection points of the two graphs.
- 🔍 The intersection points are approximately -2 and 0.78, which are used as the limits of integration.
- 📐 The vertical distance between the graphs of f and g, denoted as h(x), is used to determine whether the function h is increasing or decreasing.
- ⛏ The volume of the solid formed by the cross-section of the graphs is found by integrating the square of the vertical distance h(x) over the same bounds.
- 📉 To determine if h(x) is increasing or decreasing, the derivative h'(x) is evaluated at a specific point, in this case, x = -0.5.
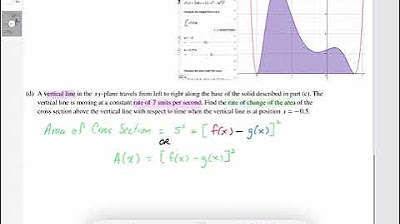
- ⏱ The rate of change of the area of the cross-section with respect to time is calculated when a vertical line moves along the base of the solid at a constant rate.
- 🔢 The rate of change is found using the derivative of the area with respect to time, considering the rate of change of x (dx/dt) is given as 7 units per second.
- 📍 The final calculation for the rate of change of the area involves substituting the function values and their derivatives at the specific point x = -0.5 into the derived formula.
- 📈 The result of the calculation for the rate of change of the area with respect to time is -9.272 square units per second, indicating a decrease in area over time.
Q & A
What is the function f(x) defined by in the script?
-The function f(x) is defined as the natural logarithm function, specifically ln(x) + 3.
What is the function g(x) in the given context?
-The function g(x) is defined as x to the fourth power plus two times x cubed, or x^4 + 2x^3.
What is the purpose of finding the area enclosed by the graphs of f and g?
-The area enclosed by the graphs of f and g is sought to understand the space between the two functions within a given interval.
How is the height of the representative rectangle determined in the script?
-The height of the representative rectangle is determined by the difference between the functions f(x) and g(x), which is f(x) - g(x).
What is the method used to find the bounds where f(x) and g(x) intersect?
-The bounds are found by setting f(x) equal to g(x) and solving for x, which gives the points of intersection.
What is the integral that represents the area between the curves of f and g?
-The integral representing the area is the integral from negative 2 to 0.78 of (f(x) - g(x)) dx.
What does the derivative of h(x) indicate about the function?
-The derivative of h(x), where h(x) = f(x) - g(x), indicates whether h(x) is increasing or decreasing.
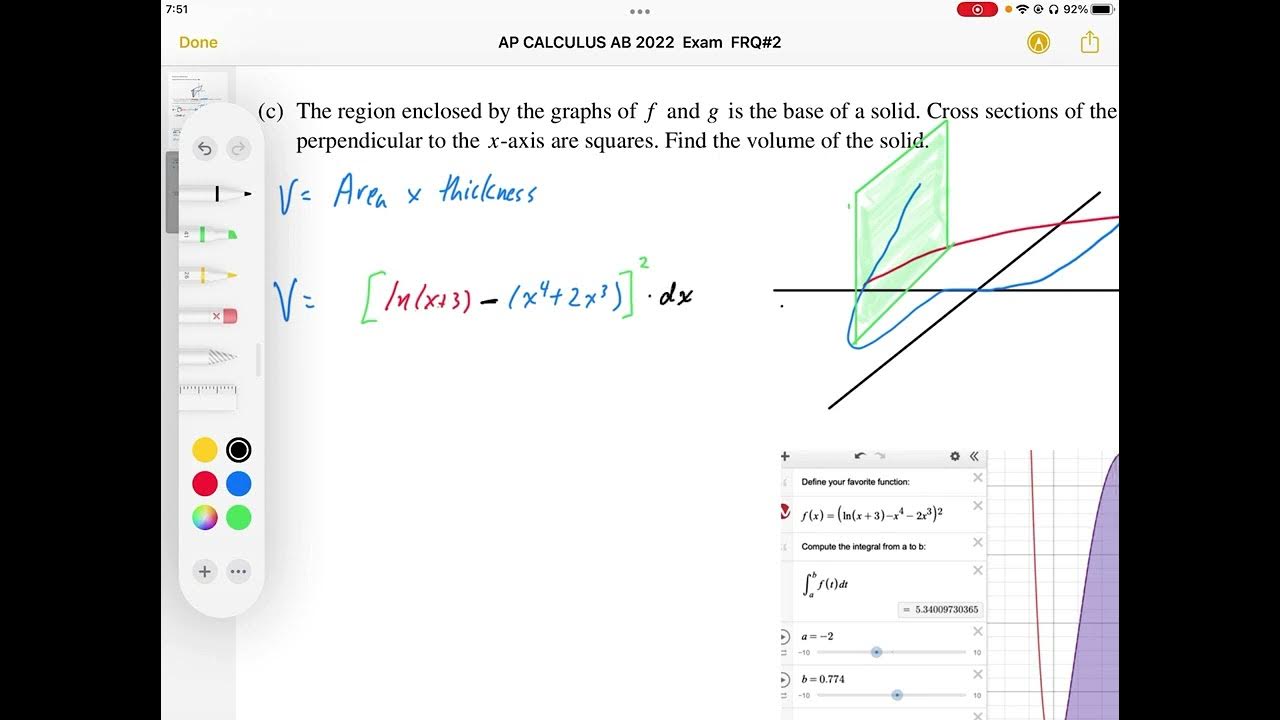
How is the volume of the solid determined in the script?
-The volume of the solid is determined by integrating the square of the vertical distance between the graphs of f and g (h(x)^2) over the bounds from negative 2 to 0.78.
What is the rate of change of the area of the cross section with respect to time when a vertical line moves at a constant rate?
-The rate of change of the area with respect to time is found by differentiating the area function a(x) = f(x) - g(x)^2 with respect to time, using the chain rule and given dx/dt, and evaluating it at x = -0.5.
What is the given rate at which the vertical line travels along the base of the solid?
-The given rate at which the vertical line travels along the base of the solid is seven units per second.
What does the final calculated rate of change of the area represent?
-The final calculated rate, negative 9.272 square units per second, represents the rate of change of the cross-sectional area of the solid with respect to time as the vertical line moves at the given constant rate.
What is the significance of the negative result in the rate of change calculation?
-A negative result indicates that the area of the cross section above the vertical line is decreasing over time as the line moves to the right.
Outlines
📊 Calculating the Area Enclosed by Two Functions
The first paragraph introduces a calculus problem involving functions f and g, defined by ln(x) + 3 and x^4 + 2x^3, respectively. The task is to find the area enclosed by the graphs of these functions. The approach involves creating a representative rectangle with the height f(x) - g(x) and integrating this expression over the bounds where the functions are equal. The intersection points of the functions are identified by plotting and calculation, which are approximately -2 and 0.78. The integration yields an area of 3.604. The paragraph also discusses whether the vertical distance h(x) = f(x) - g(x) is increasing or decreasing, concluding it is decreasing at x = -0.5. Finally, the volume of the solid formed by the cross-section of the enclosed region is calculated by integrating h(x)^2 over the bounds from -2 to 0.78, resulting in a volume of 5.340.
🚀 Rate of Change of Cross Section Area with Respect to Time
The second paragraph addresses a dynamic scenario where a vertical line moves along the base of the previously described solid at a constant rate of seven units per second. The goal is to find the rate of change of the area of the cross section above this moving line with respect to time. The area of the cross section is given by the square of the vertical distance between the graphs of f and g, a function of x. Knowing the rate of change of x (dx/dt) as seven, the paragraph uses the chain rule to find the rate of change of the area (da/dt), which involves derivatives of f and g. The final calculation, substituting x = -0.5, yields a rate of change of -9.272 square units per second.
Mindmap
Keywords
💡Functions f and g
💡Integration
💡Bounds
💡Graphs
💡Vertical Distance
💡Derivative
💡Solid of Revolution
💡Rate of Change
💡Chain Rule
💡Power Rule
💡Natural Logarithm (ln)
Highlights
The transcript discusses a calculus problem involving functions f and g, with f(x) being ln(x) + 3 and g(x) being x^4 + 2x^3.
The problem requires finding the area enclosed by the graph of f(g(x)) using integration.
A representative rectangle is used to visualize the integration process, with the height being f(x) - g(x).
The bounds for integration are determined by setting f(x) equal to g(x) and solving for x.
The intersection points of f(x) and g(x) are identified as -2 and approximately 0.78.
The area enclosed by the graphs is calculated to be 3.604 using definite integration from -2 to 0.78.
The vertical distance between the graphs f and g is denoted as h(x), which is f(x) - g(x).
The derivative of h(x) at x = -0.5 is calculated to determine if h is increasing or decreasing.
The result of the derivative shows that h(x) is decreasing because h'(-0.5) is less than 0.
The volume of the solid with the region enclosed by f and g as the base is found using the area times the thickness method.
The area for the volume calculation is h(x)^2, and the bounds are from -2 to 0.78.
The volume of the solid is calculated to be 5.340 using the given bounds and the area function h(x)^2.
A vertical line moving at a constant rate of seven units per second along the base of the solid is considered in the next part of the problem.
The rate of change of the area of the cross-section above the moving vertical line with respect to time is to be found.
The relationship between the area (a) and x is used to apply the power rule and chain rule to find da/dt.
The rate of change of the area with respect to time (da/dt) is evaluated at x = -0.5, with dx/dt given as 7 units per second.
The final calculation yields a rate of change of -9.272 square units per second for the area of the cross-section.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: