Leaning Ladder Equilibrium Problem: Find Minimum Angle

Physics Ninja

22 Sept 201923:52

EducationalLearning

32 Likes 10 Comments

TLDRIn this engaging physics problem, the speaker, known as the Physics Ninja, explores the concept of equilibrium in relation to a ladder leaning against a wall with a painter on it. The video script delves into the minimum angle at which the ladder can be set up safely for the painter to work. By drawing a Freebody diagram and applying Newton's laws, the speaker outlines the forces at play, including the weight of the ladder and the painter, the normal forces, and the static friction force. The analysis involves calculating the torque due to these forces and setting up equations to solve for the minimum angle. The speaker simplifies the problem by assuming the mass of the painter equals the mass of the ladder and provides a final calculation for the minimum angle, which is approximately 55.6 degrees. The video concludes with a discussion on the implications of varying the coefficient of static friction, demonstrating how the minimum angle would change with different frictional forces. This summary encapsulates the essence of the script, highlighting the application of physics principles to a real-world scenario.

Takeaways

🎨 The video discusses a physics problem related to the stability of a ladder leaning against a wall while a painter is working on a house trim.
🧍 The scenario involves a painter standing on a ladder at a certain distance from the wall, which is used to explore the concept of equilibrium in physics.
📐 The presenter defines an angle (θ) between the ladder and the ground, which is crucial for determining the minimum safe angle for the ladder to be set up.
🚨 A ladder set up at a very small angle (θ) is unstable and poses a risk of falling, while a ladder at a very large angle is steep and can be difficult to climb.
🤔 The goal is to find the minimum angle θ that the ladder can be set up at before it starts to slip, ensuring safety during use.
📉 The ladder's weight and the painter's weight are considered as forces acting on the ladder, which must be balanced for equilibrium.
⚖️ The coefficient of static friction between the ladder and the ground is a key factor in the problem, with a value given as 0.4 in the example.
📐 Freebody diagrams are used to illustrate all the forces acting on the ladder, including the normal forces and frictional force.
⚙️ Newton's first law (equilibrium condition) is applied to set up equations for the forces in the x and y directions and the torque about a pivot point.
🔢 The solution process simplifies the equations by substituting known values and using the relationship between static friction and the normal force.
👨‍🔧 An assumption is made that the painter's mass equals the ladder's mass to simplify calculations, resulting in a minimum angle of 55.6 degrees for the ladder.
💡 The video concludes with a sanity check by considering the limits of the coefficient of static friction to ensure the physical plausibility of the results.

Q & A

What is the main problem that the Physics Ninja is trying to solve in the script?
-The main problem is to find the minimum angle at which a painter can safely set up a ladder to paint the trim on a house without the risk of it slipping or falling.
What are the forces acting on the ladder that need to be considered for equilibrium?
-The forces acting on the ladder that need to be considered are the weight of the ladder (Mg), the weight of the painter (Mg), the normal force from the wall (N1), the normal force from the ground (N2), and the static frictional force (Ff).
What is the significance of choosing a coordinate system when solving this problem?
-Choosing a coordinate system is significant because it helps to systematically analyze the forces acting on the ladder in the horizontal (X) and vertical (Y) directions, as well as to calculate the torques that could cause rotation.
How does the position of the painter on the ladder affect the minimum angle calculation?
-The position of the painter on the ladder affects the minimum angle calculation because it determines the location of the forces acting on the ladder, specifically the weight of the painter, which influences the torque and the equilibrium conditions.
What is the role of the coefficient of static friction in this problem?
-The coefficient of static friction is crucial as it determines the maximum force of static friction that can act between the ladder and the ground, which in turn affects the stability of the ladder and the minimum angle at which it can be safely used.
Why does the Physics Ninja assume the coefficient of static friction between the ladder and the wall to be zero?
-The Physics Ninja assumes the coefficient of static friction between the ladder and the wall to be zero to simplify the problem. Including this friction would add another force to the Freebody diagram and complicate the calculations without significantly altering the main outcome related to the minimum angle.
What is the minimum angle calculated for the ladder when the mass of the painter is equal to the mass of the ladder?
-When the mass of the painter is equal to the mass of the ladder, the minimum angle calculated for the ladder is approximately 55.6 degrees.
How does the total mass of the system affect the calculation of the normal force N2?
-The total mass of the system (the painter plus the ladder) multiplied by the acceleration due to gravity (g) gives the total weight of the system, which is equal to the normal force N2 acting upwards from the ground to support the ladder.
What happens to the minimum angle if the coefficient of static friction approaches zero?
-If the coefficient of static friction approaches zero, indicating very little friction between the ladder and the ground, the minimum angle would approach 90 degrees. This is because there would be insufficient friction to prevent the ladder from slipping, even at a near-vertical position.
What happens to the minimum angle if the coefficient of static friction is very large?
-If the coefficient of static friction is very large, indicating a lot of friction between the ladder and the ground, the minimum angle would approach 0 degrees. This is because the increased friction would allow the ladder to be placed at a very shallow angle without slipping.
What is the assumption made by the Physics Ninja when taking limiting cases to check the physics of the problem?
-The Physics Ninja assumes that the mass of the painter is equal to the mass of the ladder to simplify the expression and to take limiting cases to check if the physics of the problem holds true under extreme conditions of low and high coefficients of static friction.

Outlines

00:00

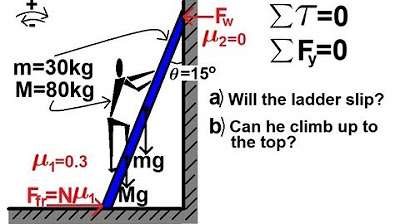
🎨 Introduction to the Ladder Stability Problem

The video begins with the Physics Ninja introducing a real-life physics problem involving a ladder used for painting a house. The ladder is positioned against a wall, and the challenge is to determine the minimum angle at which the ladder can be safely used without slipping. The narrator sets up the problem by defining the angle theta, which the ladder makes with the ground, and discusses the implications of both very small and very large angles in terms of stability and safety.

05:01

📐 Setting Up the Freebody Diagram and Forces

The narrator creates a Freebody diagram to analyze the forces acting on the ladder. The forces considered include the weight of the ladder, the weight of the painter, the normal force exerted by the wall, and the static friction force between the ladder and the ground. The coefficient of static friction is given as 0.4. The video explains that friction between the ladder and the wall is not considered in this simplified model. The forces are then broken down into components, and Newton's first law is applied to establish equilibrium conditions in both the horizontal and vertical directions, as well as in terms of torque.

10:02

🔍 Calculating Torques and Applying Newton's Law

The video continues by calculating the torque produced by each of the forces acting on the ladder. The narrator places a pivot point and calculates the torque due to the weight of the painter, the weight of the ladder, the normal force, and the frictional force. The torques are summed up, and the equation is set to equal zero to represent the ladder's equilibrium. The maximum force of static friction is linked to the normal force, and the narrator simplifies the expression by substituting the total weight of the system into the equation.

15:02

🧮 Solving for the Minimum Angle Using Static Friction

The narrator simplifies the torque equation by substituting the maximum force of static friction and eliminating the normal force n2 with the total weight of the system. The equation is further simplified by dividing through by the cosine of the angle theta, which results in an expression involving the tangent of the angle theta. The coefficient of static friction is then used to isolate and solve for the minimum angle theta, which is found to be 55.6 degrees under the assumption that the mass of the painter is equal to the mass of the ladder.

20:03

🔧 Limiting Cases and Conclusion

The video concludes by examining the limiting cases for the minimum angle. When the coefficient of static friction is very small, the minimum angle approaches 90 degrees, indicating that without friction, the ladder would need to be almost vertical to be stable. Conversely, with a large coefficient of static friction, the minimum angle can be very small, showing that a greater frictional force allows for a steeper and yet stable ladder angle. The narrator emphasizes the importance of understanding the physics behind such problems and thanks the viewers for watching.

Mindmap

Keywords

💡Equilibrium

Equilibrium in physics refers to a state in which all acting forces are balanced, resulting in no net force and no acceleration. In the context of the video, the ladder is in equilibrium when it is leaning against the wall and the painter is safely standing on it. The script discusses setting up equations to ensure the ladder remains in equilibrium to prevent slipping or falling.

💡Freebody Diagram

A freebody diagram is a graphical representation that shows all the forces acting on an object in a given situation. It is a fundamental tool in physics for visualizing and analyzing forces. The video script uses a freebody diagram to illustrate the forces acting on the ladder, including the weight of the ladder and the painter, normal forces, and frictional forces.

💡Normal Force

The normal force is the perpendicular force exerted by a surface that resists the compression of two bodies in contact with each other. In the script, the normal force is depicted as the force exerted by the wall on the ladder and by the ground on the ladder. It is crucial in maintaining the ladder's equilibrium and preventing it from slipping.

💡Friction

Friction is the force that resists the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. The script discusses static friction, which is the friction between two solid objects that are not moving relative to each other. It plays a vital role in keeping the ladder stationary against the wall and the ground.

💡Coefficient of Static Friction

The coefficient of static friction is a dimensionless scalar value that represents the maximum possible frictional force that can be achieved between two contacting surfaces before the relative motion between them begins. In the video, it is given as 0.4 and is used to calculate the maximum static friction force that can act on the ladder.

💡Torque

Torque is the rotational equivalent of linear force. It is a measure of the force that can cause an object to rotate about an axis. The video script discusses the torques acting on the ladder due to the various forces, such as the weight of the painter and the ladder itself, and how these torques must sum to zero for the ladder to remain in equilibrium.

💡Newton's First Law

Newton's first law, also known as the law of inertia, states that an object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force. The script applies this law to ensure that the forces and torques acting on the ladder are balanced, resulting in no acceleration and a stable position.

💡Mass

Mass is a measure of the amount of matter in an object. In the context of the video, the mass of the painter and the ladder are considered when calculating the forces and torques. The script mentions the painter's mass as uppercase M and the ladder's mass as lowercase M, which are used to calculate weights and normal forces.

💡Ladder Length

The length of the ladder (denoted as L in the script) is a critical parameter in the calculations for the forces and torques acting on the ladder. The script specifies that the painter is standing at 2/3 of the total ladder length, which affects the distribution of forces and the calculation of the minimum safe angle for the ladder.

💡Minimum Angle

The minimum angle is the smallest angle at which the ladder can be safely set up against the wall without slipping, given the conditions and forces involved. The video aims to calculate this angle using the principles of physics and the provided parameters. The script concludes that with the given conditions, the minimum angle is approximately 55.6 degrees.

💡Static Equilibrium

Static equilibrium refers to the condition where all forces and torques acting on an object are balanced, resulting in no motion. The entire analysis in the video script is focused on achieving static equilibrium for the ladder to ensure safety while the painter is working on it.

Highlights

The video presents a physics problem involving a ladder leaning against a house, with a painter standing on it.

The problem is to determine the minimum angle at which the ladder can be safely set up to prevent slipping.

Freebody diagrams are used to analyze the forces and torques acting on the ladder.

The ladder's angle with respect to the ground is denoted as theta.

The ladder's weight and the painter's weight are considered as forces acting on the ladder.

The coefficient of static friction between the ladder and the ground is given as 0.4.

The painter is positioned at 2/3 of the ladder's length from the bottom.

Newton's first law of motion is applied to establish equilibrium conditions for the forces and torques.

The total mass of the system (painter plus ladder) is used to calculate the normal force.

Torque calculations involve the perpendicular components of the forces and their distances from the pivot point.

The force of friction is considered to prevent the ladder from sliding and is maximized for the minimum angle calculation.

The minimum angle is found by solving the equation involving the tangent of theta, the total mass, and the coefficient of static friction.

An assumption is made that the mass of the painter equals the mass of the ladder for simplification.

The minimum angle theta is calculated to be approximately 55.6 degrees under the assumption.

Limiting cases are considered to validate the physics, such as when the coefficient of static friction is very small or very large.

The video concludes with a practical understanding of how to solve similar physics problems involving equilibrium and forces.

Transcripts

Browse More Related Video

The Leaning Ladder Problem | Physics with Professor Matt Anderson | M12-22

Physics 15 Torque Example 7 (7 of 7) The Ladder Problem (should be cos(15) at end)

Torque Example #3: Leaning Ladder Problem

Ladder Example for Static Equilibrium

Maximum Speed Around a Banked Curve WITH Friction

Banked Curve with Friction: Finding Maximum and Minimum Speed

Related Tags

Ladder Safety Physics Problem Equilibrium Forces and Torques Static Friction Newton's Laws Freebody Diagram Safety Angle Home Improvement Physical Calculation