The Leaning Ladder Problem | Physics with Professor Matt Anderson | M12-22
TLDRIn this engaging video, Dr. Anderson introduces the Leaning Ladder Problem, a physics scenario involving a ladder leaning against a wall with friction on the floor. The problem explores how far up the ladder a person can climb before it slips and falls. The video script delves into the forces and torques acting on the ladder, using a force diagram to illustrate the static frictional force, the weight of the ladder and person, and the push from the wall. By selecting an axis of rotation at the ground, the video simplifies the torque analysis, considering the lever arms of the ladder's weight, the person's weight, and the wall's push. The challenge is to solve for the unknowns, including the maximum distance 'x' a person can climb, using the given equations and the static friction equation. The video encourages students to tackle the problem and seek help if needed, fostering an interactive learning experience.
Takeaways
- 📏 The Leaning Ladder Problem involves a ladder leaning against a wall with friction on the floor.
- 🧱 The wall is frictionless, and the ladder's stability is affected by how high a person can climb before it slips.
- 🎛️ The ladder has a length (l), and the person is at a distance (x) up the ladder, forming an angle (θ) with the floor.
- 📐 At the base of the ladder, there is a normal force (N), static frictional force (f_s), and the wall exerts a push (P) at the top.
- 🚫 The forces in the (x) direction are (f_s) to the right and the person's weight to the left, which must sum to zero.
- 🚫 The forces in the (y) direction include the normal force (N), the weight of the ladder (m_l ⋅ g), and the person's weight, also summing to zero.
- ⚖️ Torques acting on the ladder are considered about the ground contact point as the axis of rotation.
- ↔️ The weight of the ladder contributes a torque with a lever arm (l/2) times (cos(θ)).
- ↔️ The person's weight contributes a torque with a lever arm (x) times (cos(θ)).
- ↕️ The push (P) from the wall has a lever arm (l) times (sin(θ)) and contributes positively to the torque.
- 🔢 To solve for (x), the maximum height a person can climb, four equations are needed, including the static friction limit (f_s = μ_s ⋅ N).
- 🤔 The problem requires setting up and solving a system of equations involving forces and torques to find the critical climb height.
Q & A
What is the leaning ladder problem?
-The leaning ladder problem involves a ladder leaning against a wall with friction on the floor. The challenge is to determine how far up the ladder a person can climb before the ladder slips and falls.
What are the forces acting on the ladder?
-The forces acting on the ladder include the normal force (N), static frictional force (Fs), the weight of the ladder (m_l * g), the weight of the person (m_p * g), and the push from the wall (P).
What is the significance of choosing an axis of rotation when calculating torques?
-Choosing an axis of rotation simplifies the calculation of torques by eliminating forces that pass through the axis and therefore do not contribute to the torque about that point.
How does the friction on the floor affect the ladder's stability?
-The static friction on the floor helps to keep the bottom of the ladder in place, preventing it from slipping. The coefficient of friction (μs) determines the maximum force of friction that can act.
What is the role of the wall in the stability of the ladder?
-The wall provides a reaction force (push P) at the top of the ladder, which contributes to the torques acting on the ladder and affects its stability.
What is the relationship between the ladder's length, the person's climb, and the angle θ?
-The ladder has a length (l), the person is a distance (x) up the ladder, and the angle between the ladder and the floor is θ. These variables are interconnected in the force and torque equations that determine the ladder's stability.
How do you calculate the torque due to the weight of the ladder?
-The torque due to the weight of the ladder is calculated by multiplying the weight of the ladder (m_l * g) by the lever arm, which is the distance from the axis of rotation to the line of action of the force, in this case, l * cos(θ)/2.
What is the maximum value of static friction that can act on the ladder?
-The maximum static friction (Fs) that can act on the ladder is μs times the normal force (N), where μs is the coefficient of static friction.
What are the equations needed to solve for the maximum distance x a person can climb?
-To solve for x, you need the equations for the sum of forces in the x and y directions to be zero, the torque equation about the axis of rotation to be zero, and the static friction equation.
What is the significance of the lever arm in calculating torques?
-The lever arm is the perpendicular distance from the axis of rotation to the line of action of the force. It determines the effectiveness of the force in producing torque; the longer the lever arm, the greater the torque for a given force.
How does the weight of the person affect the ladder's stability?
-The weight of the person contributes to the torques acting on the ladder and affects its stability. The lever arm for the person's weight is x * cos(θ), and as the person climbs higher (x increases), the torque due to their weight also increases.
What additional information is needed to solve for the unknowns in the problem?
-To solve for the unknowns (fs, p, n, and x), you need the four equations derived from the force and torque balances, along with the static friction equation, and any given values for the ladder's length (l), the person's mass (m_p), the ladder's mass (m_l), and the coefficient of friction (μs).
Outlines
📐 Introduction to the Leaning Ladder Problem
This paragraph introduces the leaning ladder problem, a physics scenario where a ladder of length 'l' leans against a frictionless wall and rests on a floor with friction having a coefficient of friction μs. The problem explores how far up the ladder a person can climb before it becomes unstable and slips. The forces acting on the ladder include the normal force 'N', static frictional force 'f_s', the weight of the ladder 'm_l * g', the weight of the person 'n_p * g', and the push 'P' from the wall. The paragraph sets up the problem by describing the forces and torques involved, choosing a point at the ground as the axis of rotation to simplify the torque analysis.
🔍 Analyzing Forces and Torques on the Ladder
The second paragraph delves into the forces and torques acting on the ladder in more detail. It discusses the equilibrium conditions in the x and y directions, where the sum of forces in both directions must equal zero. The paragraph then focuses on calculating the torques around the chosen axis of rotation. It identifies the torques due to the weight of the ladder (with a lever arm of l/2 * cos(θ)), the weight of the person (with a lever arm of x * cos(θ)), and the push from the wall (with a lever arm of l * sin(θ)). The paragraph concludes by noting that an additional equation, the static friction equation (f_s = μs * N), is needed to solve for the unknowns, including the maximum distance 'x' a person can climb before the ladder slips.
Mindmap
Keywords
💡Leaning Ladder Problem
💡Friction
💡Coefficient of Friction (μs)
💡Normal Force (N)
💡Static Frictional Force (fs)
💡Weight of the Ladder (mlg)
💡Weight of the Person (npg)
💡Push from the Wall (P)
💡Torque
💡Lever Arm
💡Equilibrium
💡Angle Theta (θ)
Highlights
Dr. Anderson introduces the leaning ladder problem, a common scenario involving physics and stability.
The setup includes a floor, a wall, and a ladder leaning against the wall with friction on the floor.
The problem explores how far a person can climb before the ladder slips and falls.
The ladder's length is denoted as 'l', and the person's height on the ladder as 'x'.
The angle between the ladder and the floor is represented as 'theta'.
Forces and torques acting on the ladder are considered, including normal force 'N', static frictional force 'f_s', and the weight of the ladder and person.
The wall exerts a push 'P' on the top of the ladder, which is also a force to consider.
The sum of forces in the x-direction and y-direction must add up to zero for equilibrium.
Torque calculations require choosing an axis of rotation, which is the ground contact point in this case.
The weight of the ladder contributes a torque with a lever arm of l/2 * cos(theta).
The person's weight contributes a torque with a lever arm of x * cos(theta).
The push 'P' from the wall creates a positive torque with a lever arm of l * sin(theta).
The sum of all torques must equal zero for the ladder not to rotate.
Four unknowns (fs, P, n, and x) require four equations for solving.
The static friction equation, f_s = mu_s * N, is the fourth equation needed.
With the four equations, one can solve for 'x' to determine the maximum height a person can climb.
Dr. Anderson offers help to students struggling with the problem and encourages them to visit during office hours.
Transcripts
Browse More Related Video

Torque Example #3: Leaning Ladder Problem

Ladder Example for Static Equilibrium
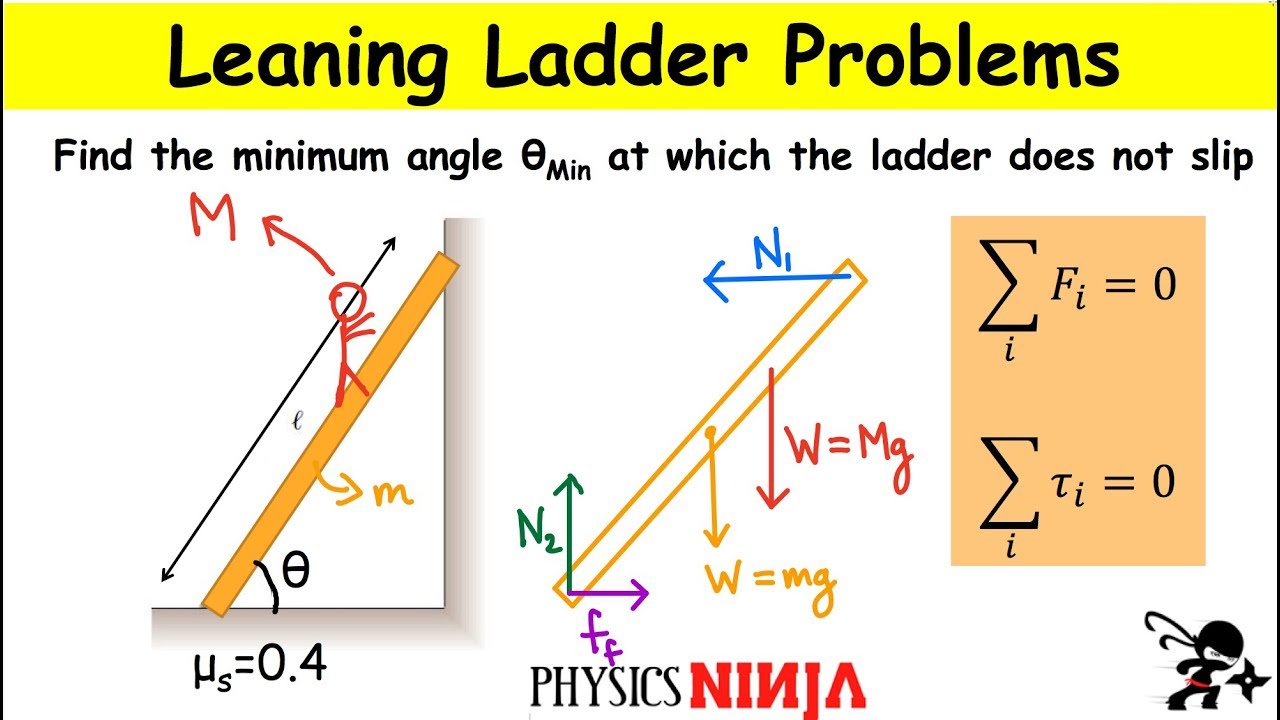
Leaning Ladder Equilibrium Problem: Find Minimum Angle
Physics 15 Torque Example 7 (7 of 7) The Ladder Problem (should be cos(15) at end)
Physics 15 Torque (21 of 25) More Examples: 3 T=? of Cable of Step Ladder

Solving a falling ladder problem using related rates
5.0 / 5 (0 votes)
Thanks for rating: