The Chain Rule for Partial Derivatives — Topic 73 of Machine Learning Foundations

Jon Krohn
27 Oct 202109:23
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the application of the chain rule for partial derivatives in the context of multivariate functions, a concept integral to machine learning. It begins by reviewing the chain rule for full derivatives with nested univariate functions, illustrating how to compute the full derivative (dy/dx) by multiplying the derivatives of the nested functions. The script then transitions to the more complex scenario of multivariate functions, where the chain rule becomes particularly relevant. It explains how to calculate partial derivatives for a function of multiple variables by diagramming the relationships between variables, which simplifies the process of tracing and summing the individual contributions to the overall derivative. The video emphasizes the utility of visual diagrams for understanding and computing partial derivatives, especially in scenarios involving multiple layers of nested functions. The general formula for the complete partial derivative is also presented, highlighting the summation of all individual paths from the output to any given input variable. The script concludes with exercises to reinforce the viewer's understanding of the chain rule.

Takeaways
  • 📚 The chain rule for full derivatives is a fundamental concept covered in the 'Machine Learning Foundation' series, which is essential for understanding how to extend it to partial derivatives.
  • 🔗 In nested univariate functions, the chain rule for full derivatives allows us to calculate the derivative of y with respect to x by multiplying the derivative of y with respect to an intermediate variable u, by the derivative of u with respect to x.
  • 📈 Partial derivatives in the context of univariate functions nested within each other would be identical to the full derivative, given there's only one input variable involved.
  • 🤔 The real utility of partial derivatives emerges when dealing with multivariate functions, where the chain rule becomes more complex and essential for calculations.
  • 📊 Diagrams or 'trees' representing the relationships between variables can greatly simplify the process of understanding and calculating partial derivatives in multivariate functions.
  • 🌐 For a multivariate function g with inputs x and z, which is nested inside another function f yielding y, the chain rule helps to calculate the partial derivatives by breaking down the problem into simpler steps.
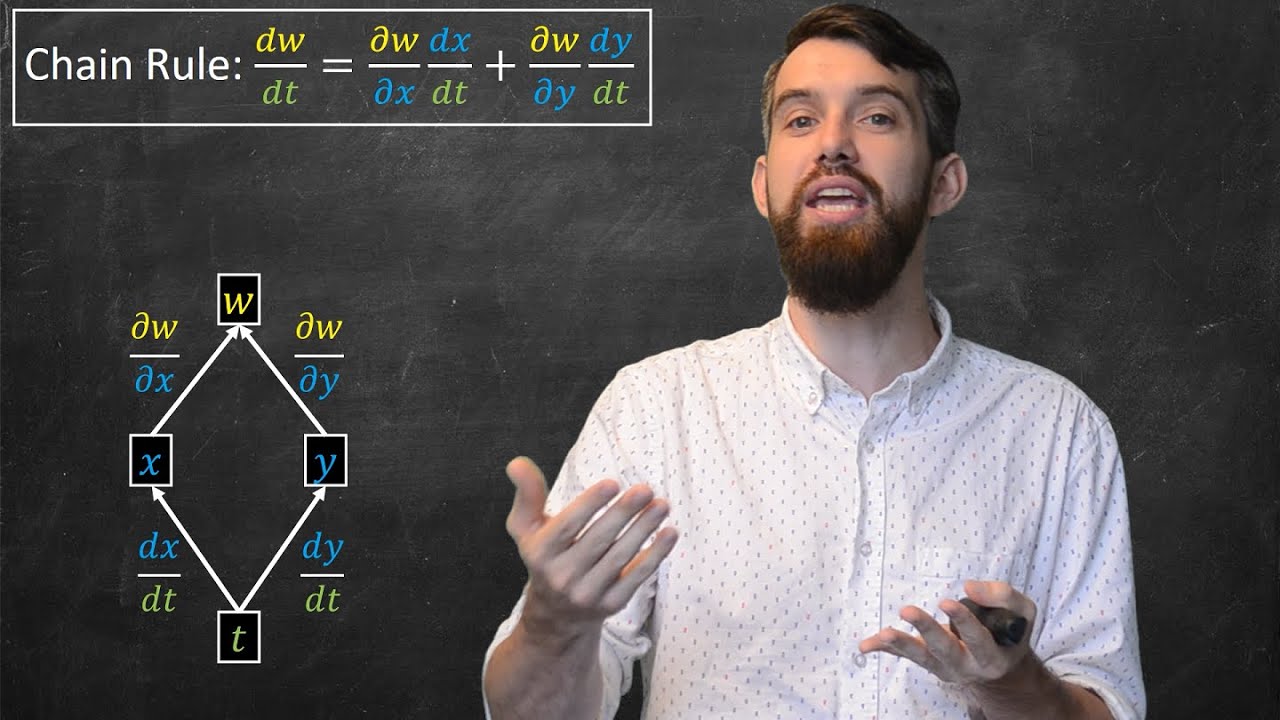
  • 🔍 To find the partial derivative of y with respect to x (del y/del x), one must calculate the partial derivatives of the intermediate steps and then multiply them, summing any contributions from different paths leading to x.
  • 🔁 The process of calculating partial derivatives involves summing the products of the partial derivatives along each path from the output variable back to the input variable of interest.
  • 🌳 A tree diagram helps visualize the dependencies between variables, making it easier to trace the paths needed to calculate the partial derivatives.
  • 🔢 When calculating partial derivatives for a function of multiple variables, one must consider all the paths through which the output variable depends on the input variable of interest.
  • 🧮 The general formula for the complete partial derivative of y with respect to an input xi, involves summing the products of all the partial derivatives along each path from y to xi through any intermediate variables.
  • 📝 Memorizing the general formula is not as crucial as understanding the process and being able to apply it intuitively, which can be facilitated through practice with various examples.
Q & A

  • What is the chain rule for full derivatives?

    -The chain rule for full derivatives allows us to compute the derivative of a composite function. It states that if y is a function of u, and u is a function of x, then the derivative of y with respect to x (dy/dx) can be found by multiplying the derivative of y with respect to u (dy/du) by the derivative of u with respect to x (du/dx), which eliminates the 'u' terms.

  • Why might the partial derivative be the same as the full derivative in a certain situation?

    -In a situation where there is a nested univariate function inside another univariate function, the partial derivative would be identical to the full derivative because there are no other variables involved. This is an unusual case, as partial derivatives are more commonly used with multivariate functions.

  • How does the chain rule for partial derivatives help in machine learning?

    -In machine learning, the chain rule for partial derivatives is crucial for backpropagation, which is a common method for training neural networks. It allows for the calculation of gradients of a loss function with respect to the parameters of the network, even when the function involves many layers or steps.

  • What is the significance of creating a diagram or 'tree' to represent the relationships between variables in a multivariate function?

    -Creating a diagram or 'tree' helps visualize the flow of variables and the dependencies between them. This makes it easier to understand and calculate partial derivatives, especially in complex scenarios where there are multiple layers of nested functions.

  • How do you calculate the partial derivative of y with respect to x (∂y/∂x) when y depends on multiple variables u and v, which are both functions of x and z?

    -To calculate ∂y/∂x, you trace down both the u and v branches of the dependency tree to reach x. You calculate the partial derivatives ∂y/∂u * ∂u/∂x for the u branch and ∂y/∂v * ∂v/∂x for the v branch, and then sum these two contributions to get the overall partial derivative ∂y/∂x.

  • What does the general formula for the partial derivative of y with respect to xi represent?

    -The general formula for the partial derivative of y with respect to xi (∂y/∂xi) represents the sum of all individual contributions to the change in y due to a change in xi. Each contribution is a product of the partial derivative of y with respect to an intermediate variable uj and the partial derivative of that intermediate variable uj with respect to xi.

  • How does the chain rule for partial derivatives apply when there are multiple layers of multivariate functions?

    -When there are multiple layers of multivariate functions, the chain rule for partial derivatives becomes more complex but also more powerful. It allows for the calculation of the overall effect on the output variable y due to changes in any of the input variables xi, taking into account all intermediate steps and dependencies.

  • What is the role of the chain rule in calculating the partial derivatives of nested multivariate functions?

    -The chain rule is essential for breaking down the process of calculating partial derivatives of nested multivariate functions into simpler steps. It allows us to compute the partial derivatives of the outer function with respect to the inner functions and then multiply these by the partial derivatives of the inner functions with respect to the variables of interest.

  • How does the cancellation of intermediate variables (like u) in the chain rule simplify the calculation of partial derivatives?

    -The cancellation of intermediate variables simplifies the calculation by reducing the complexity of the expression. When you multiply the partial derivatives, the intermediate variables (like u) appear in both the numerator and the denominator, and they cancel each other out, leaving a simplified expression that only involves the variables of direct interest.

  • What is the practical application of understanding the chain rule for partial derivatives in the field of mathematics and engineering?

    -Understanding the chain rule for partial derivatives is crucial in fields that involve complex systems with multiple interconnected variables, such as physics, engineering, and economics. It is used to analyze how changes in one part of the system affect other parts and to optimize designs and processes.

  • Can you provide an example of how the chain rule for partial derivatives would be used in a real-world scenario?

    -In meteorology, the chain rule could be used to understand how a change in temperature (x) might affect the formation of a weather pattern (y), which itself depends on factors like humidity (u) and wind speed (v). By applying the chain rule, we can quantify the indirect effect of temperature on the weather pattern through its effects on humidity and wind speed.

  • What is the importance of understanding the chain rule for students learning calculus?

    -Understanding the chain rule is fundamental for students learning calculus as it extends their ability to find derivatives to more complex functions. It is a gateway to solving problems involving composite functions, which are common in higher-level mathematics and applications across various scientific disciplines.

Outlines
00:00
📚 Introduction to Chain Rule for Partial Derivatives

The video begins by assuming the viewer is already familiar with the chain rule for full derivatives, a topic previously covered in another video. It then transitions into an exploration of the chain rule as it applies to partial derivatives of multivariate functions. The presenter explains that while the chain rule for full derivatives is straightforward with nested univariate functions, the real complexity arises when dealing with multivariate functions. The video uses diagrams to illustrate the flow of variables and emphasizes the importance of understanding how to calculate partial derivatives within these complex structures. It concludes by demonstrating how to calculate the partial derivative del y/del x by multiplying the partial derivatives del u/del x and del y/del u, after which the del u terms cancel out.

05:01
🌐 Multivariate Chain Rule and Variable Relationships

This paragraph delves into the multivariate chain rule, focusing on scenarios where a variable, such as y, depends on multiple other variables, u and v, which themselves are functions of x and z. The presenter suggests visualizing the relationships between variables using a tree diagram to simplify the calculation of partial derivatives. The process involves tracing the path from the output variable back to the input variable of interest, summing the contributions from each path. The video provides a general formula for calculating the complete partial derivative of y with respect to any input xi, emphasizing the summation of all individual paths (or 'legs') that connect y to xi through intermediate variables. The presenter also mentions that understanding this concept intuitively is more important than memorizing the formula, and teases upcoming exercises to test the viewer's comprehension of the chain rule.

Mindmap
Keywords
💡Chain Rule
The Chain Rule is a fundamental principle in calculus for finding derivatives of composite functions. It allows the derivative of a function to be found by relating it to the derivatives of its components. In the video, the Chain Rule is extended to partial derivatives of multivariate functions, which is crucial for understanding how changes in one variable affect another in complex, nested functions, as often encountered in machine learning.
💡Full Derivatives
Full derivatives, also known as total derivatives, represent the rate of change of a function with respect to a variable, taking into account all possible ways that variable can change. In the context of the video, full derivatives are initially discussed in the case of univariate functions and later extended to multivariate functions, which is essential for machine learning algorithms that deal with multiple variables.
💡Partial Derivatives
Partial derivatives are a concept from multivariate calculus that measure how a function changes with respect to a single variable while holding the other variables constant. The video emphasizes their importance in machine learning, particularly when dealing with multivariate functions, as they help in understanding the sensitivity of a function's output to each input variable.
💡Multivariate Functions
Multivariate functions are mathematical functions that take multiple variables as inputs and return a single output. The video discusses how to apply the chain rule to these functions, which is a key concept in machine learning where models often depend on multiple input features.
💡Nested Functions
Nested functions refer to functions within functions, where the output of one function is used as an input to another. In the video, nested functions are used to illustrate the application of the chain rule. Understanding nested functions is vital for tracing back through complex machine learning models to understand how changes in input variables propagate through the model to affect the output.
💡Machine Learning Foundation
The term refers to the basic principles and concepts that underpin machine learning. The video is part of a series that covers these foundational topics, with a focus on the mathematical underpinnings necessary for understanding how machine learning algorithms work, particularly in the context of derivatives and function composition.
💡Derivative Calculation
Derivative calculation is the process of finding the derivative of a function, which represents the sensitivity or rate of change of the function with respect to its variables. The video script explains how to calculate derivatives for nested and multivariate functions, which is a fundamental skill for anyone working with machine learning models.
💡Variable Diagrams
Variable diagrams, also known as dependency diagrams, are visual representations that illustrate the relationships between different variables in a function. In the video, these diagrams are recommended for breaking down complex multivariate functions to make calculating partial derivatives easier. They are particularly useful for understanding the chain of dependencies in nested functions.
💡Univariate Functions
Univariate functions are functions with a single input variable. The video script begins with a discussion of univariate functions to introduce the concept of derivatives and the chain rule before moving on to more complex multivariate functions. Univariate functions serve as a simpler case to understand the basic principles that are later extended to multivariate scenarios.
💡Generalization
Generalization in the context of the video refers to the process of extending a concept from a specific case to a broader set of scenarios. The video generalizes the chain rule from simple univariate functions to more complex multivariate functions, which is essential for applying these mathematical concepts to a wide range of problems in machine learning.
💡Exercises
The video script mentions exercises to test comprehension, which are practical applications of the concepts discussed. These exercises are designed to reinforce the viewer's understanding of the chain rule and its application to partial derivatives in multivariate functions, a common practice in educational content to ensure the material is well understood.
Highlights

The video assumes familiarity with the chain rule for full derivatives, which is essential for understanding the extension to partial derivatives of multivariate functions.

The chain rule for full derivatives is extended to partial derivatives, which is crucial for machine learning applications involving nested functions.

Nested univariate functions can be represented as a chain where the full derivative is calculated by multiplying the derivatives of the individual nested functions.

In the case of univariate functions nested within each other, the full derivative is equal to the partial derivative due to the lack of other variables involved.

Partial derivatives are more commonly used with multivariate functions, where the chain rule becomes particularly relevant.

A multivariate function with two inputs x and z is introduced, which is used to calculate the partial derivatives.

The concept of diagramming the flow of variables is emphasized for better understanding and calculation of partial derivatives.

The partial derivative of y with respect to x is calculated by multiplying the partial derivatives of u with respect to x and y with respect to u.

A similar approach is used to calculate the partial derivative of y with respect to z, demonstrating the versatility of the method.

The chain rule becomes more complex with multiple multivariate functions, requiring the creation of a tree to represent the relationships between variables.

The partial derivative of y with respect to x is calculated by summing the contributions from each branch of the variable tree.

The generalization of the chain rule for partial derivatives is presented, showing how to calculate the partial derivative of y with respect to any variable xi.

The importance of understanding the chain rule intuitively is emphasized, rather than memorizing the formula.

Exercises are provided to test the viewer's comprehension of the chain rule for partial derivatives.

The video provides a comprehensive guide to understanding and applying the chain rule for partial derivatives in machine learning.

The chain rule is fundamental for navigating through complex nested functions in machine learning models.

The video demonstrates how to break down chained multivariate functions to simplify the calculation of partial derivatives.

A step-by-step approach is used to calculate partial derivatives, making the process more accessible for learners.

Transcripts

Browse More Related Video

Partial Derivatives - Multivariable Calculus

The Chain Rule for Derivatives — Topic 59 of Machine Learning Foundations

The Multi-Variable Chain Rule: Derivatives of Compositions

Multivariable Chain Rule (Calculus 3)

1.7 - The Chain Rule

The Chain Rule for Derivatives in Calculus - [1-5]

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Chain RulePartial DerivativesMultivariate FunctionsMachine LearningFull DerivativesNested FunctionsDerivative CalculationUnivariate FunctionsVariable DependenciesDiagrammatic AnalysisDerivative Summation