The Product Rule for Derivatives — Topic 57 of Machine Learning Foundations
TLDRThe video script delves into the Product Rule, a fundamental concept in calculus that allows for the differentiation of products of two functions. It explains that when dealing with a product of two variables, such as w and z, the Product Rule can be applied to find the derivative by splitting the computation into two parts: one part involves the derivative of z multiplied by w, and the other part involves z multiplied by the derivative of w. The script illustrates this with a numerical example, where y is a function of the product of 6x^3 (w) and 7x^4 (z). Using the power rule and constant multiple rule, the derivatives of w and z are calculated separately, and then combined using the Product Rule to find dy/dx. The process simplifies to finding the sum of two terms, both involving x to the power of 6, resulting in a final expression of 168x^6 + 126x^6. The script concludes by noting the utility of the Product Rule in simplifying complex calculations and hints at the Quotient Rule, another important differentiation rule.
Takeaways
- 📚 The Product Rule allows us to find the derivative of a product of two functions by differentiating each function separately and combining the results.
- 🔍 If we have two variables, w and z, the Product Rule states that the derivative of their product can be split into two terms: w times the derivative of z and z times the derivative of w.
- ✅ The Product Rule simplifies calculations involving multiple differentiation rules, making complex expressions more manageable.
- 📈 The rule is particularly useful when the product of functions is incalculable before differentiation.
- 🌟 An example given in the script involves the function y as a product of 6x^3 (w) and 7x^4 (z), demonstrating the application of the Product Rule.
- 🧮 Using the Power Rule and Constant Multiple Rule, the derivatives of w and z are calculated as 18x^2 and 28x^3, respectively.
- 📝 The final derivative of y, or dy/dx, is found by applying the Product Rule and substituting the calculated derivatives of w and z.
- 🔢 The calculation results in two terms involving x to the power of 6, which can be combined to yield the final simplified derivative.
- 🤓 The Product Rule is a fundamental concept in calculus that helps in solving a wide range of problems involving the differentiation of products of functions.
- 🔗 The Quotient Rule, mentioned at the end of the script, is another important rule in calculus that is closely related to the Product Rule and is used for differentiating quotients of functions.
- 📌 Memorizing and understanding the Product Rule is crucial for success in calculus, as it is a frequently used tool for solving more complex problems.
Q & A
What is the product rule in calculus?
-The product rule is a formula used to find the derivative of a product of two functions. It states that the derivative of the product of two functions w and z is the derivative of w times z plus w times the derivative of z.
How does the product rule help in simplifying calculations?
-The product rule simplifies calculations by allowing us to compute the derivative of two variables separately, which can make the process more manageable, especially when dealing with complex expressions or multiple different rules.
What are the two terms in the product rule?
-The two terms in the product rule are: (1) the first function (w) multiplied by the derivative of the second function (z) with respect to x, and (2) the second function (z) multiplied by the derivative of the first function (w) with respect to x.
How is the power rule applied in the example given in the transcript?
-In the example, the power rule is used to find the derivatives of w and z separately. For w = 6x^3, the derivative is 18x^2, and for z = 7x^4, the derivative is 28x^3. The power rule states that the derivative of x^n is nx^(n-1).
What is the constant multiple rule, and how is it used in the example?
-The constant multiple rule states that the derivative of a constant times a function is the constant times the derivative of the function. In the example, the constants 6 and 7 are brought in front of the x terms when applying the power rule to find the derivatives of w and z.
What is the final expression for the derivative of y in the given example?
-The final expression for the derivative of y (dy/dx) in the example is 2x^6 + 168x^6, which simplifies to 170x^6 after combining like terms.
How does the product rule apply when the product is incalculable before differentiation?
-The product rule is particularly useful when the product of two functions is incalculable before differentiation, as it allows us to find the derivative by breaking down the product into two separate components and finding their derivatives individually.
What is the quotient rule, and how is it related to the product rule?
-The quotient rule is another differentiation rule used to find the derivative of a quotient of two functions. It is related to the product rule as both deal with operations involving two functions. While the product rule is for multiplying functions, the quotient rule is for dividing them.
Why is it necessary to add the exponents when multiplying terms with the same base in the example?
-When multiplying terms with the same base, the exponents are added according to the laws of exponents. This is a fundamental property that allows us to simplify expressions and find the resulting power after multiplication, as demonstrated in the example with x^3 * x^4 = x^(3+4) = x^7.
How does the product rule help in managing complex derivative calculations?
-The product rule helps manage complex derivative calculations by breaking down the process into simpler steps. It allows us to find the derivatives of individual parts of a product first and then combine them, which can be less daunting and more systematic than trying to find the derivative of the entire product at once.
What is the significance of the product rule in higher-level calculus and mathematical problem-solving?
-The product rule is significant in higher-level calculus and mathematical problem-solving as it is a fundamental tool for differentiating more complex functions, which often involve products of simpler functions. It is a building block for understanding more advanced concepts and solving more intricate problems in calculus.
Can you provide a step-by-step guide on how to apply the product rule?
-To apply the product rule, follow these steps: (1) Identify the two functions being multiplied (w and z). (2) Calculate the derivative of the first function (dw/dx). (3) Calculate the derivative of the second function (dz/dx). (4) Apply the product rule formula: d(wz)/dx = w * (dz/dx) + z * (dw/dx). (5) Substitute the derivatives and any given values into the formula and simplify the expression to find the final derivative.
Outlines
📚 Understanding the Product Rule
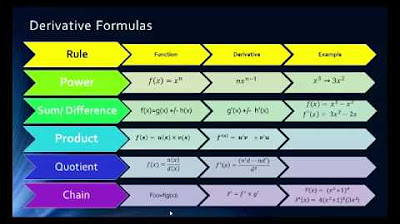
The Product Rule is a mathematical principle that allows us to differentiate the product of two functions. It is particularly useful when dealing with complex expressions that cannot be easily calculated before differentiation. The rule states that the derivative of the product of two variables, w and z, can be broken down into two separate terms: the first term is the derivative of z with respect to x, multiplied by w, and the second term is the derivative of w with respect to x, multiplied by z. This rule simplifies the differentiation process by allowing us to handle each variable independently. For example, if y is a function of the product of 6x^3 (w) and 7x^4 (z), we can find the derivatives of w and z separately using the power rule and constant multiple rule. The derivatives are dw/dx = 18x^2 and dz/dx = 28x^3. By applying the product rule, we can then calculate the derivative of y (dy/dx) as the sum of two terms: (6x^3 * 28x^3) + (7x^4 * 18x^2), which simplifies to 168x^6 + 126x^6, resulting in a final answer of 294x^6.
Mindmap
Keywords
💡Product Rule
💡Derivative
💡Variables
💡Power Rule
💡Constant Multiple Rule
💡Exponents
💡Calculus
💡Differentiation
💡Function
💡Quotient Rule
💡Simplifying
Highlights
The product rule allows for the separate computation of the derivative of two variables.
The rule can be applied when variables w and z are multiplied together.
The product rule is expressed as the sum of w times the derivative of z and z times the derivative of w.
It simplifies calculations involving multiple differentiation rules.
The product rule is especially useful when the product of functions is incalculable before differentiation.
An example is provided to illustrate the application of the product rule.
The function y is defined as the product of 6x cubed (w) and 7x to the power of 4 (z).
Derivatives of w and z are calculated separately using the power rule.
The derivative of w (dw/dx) is found to be 18x squared.
The derivative of z (dz/dx) is calculated to be 28x cubed.
The product rule is then used to find the derivative of y (dy/dx).
The resulting derivative is expressed as a sum of two terms involving w, z, dw/dx, and dz/dx.
The final answer for dy/dx is obtained by combining like terms and simplifying.
The quotient rule is introduced as a related rule to the product rule.
The quotient rule is mentioned as the next topic to be discussed.
The transcript provides a clear, step-by-step explanation of the product rule.
The use of the power rule and constant multiple rule in calculating derivatives is emphasized.
The process of adding exponents when multiplying terms with the same base is explained.
The transcript concludes with a teaser for the quotient rule, suggesting a continuation of the mathematical discussion.
Transcripts
Browse More Related Video

The Quotient Rule for Derivatives — Topic 58 of Machine Learning Foundations

Product Rule | MIT 18.01SC Single Variable Calculus, Fall 2010

Implicit Differentiation: Knowing Dependent and Independent Variables

BusCalc 11 Derivative Product Rule
Math 1325 Lecture 9 7 - Using Derivative Forumulas

Logarithmic Differentiation | Example: x^sinx
5.0 / 5 (0 votes)
Thanks for rating: