Ep12 Flory Huggins Entropy and Enthalpy - UC San Diego - NANO 134 Darren Lipomi

Darren Lipomi

1 May 201746:56

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture delves into the thermodynamics of polymer solutions, contrasting ideal and real-world scenarios. It introduces the Flory-Huggins theory, which accounts for the entropy and enthalpy changes in mixing polymers and solvents. The concept of interaction parameters and their impact on phase separation is explored, highlighting how differing intermolecular forces and increasing molecular weight affect solubility. The lecture promises a continuation with graphical analysis and phase diagrams to illustrate phase behavior in polymer solutions.

Takeaways

🧪 The ideal solution concept assumes molecules of different components have the same size and similar intermolecular forces, leading to no change in enthalpy during mixing.
📚 The Flory-Huggins Theory introduces changes to the ideal solution model by considering a polymer as one of the components, affecting the entropy of mixing and introducing the possibility of phase separation.
🔍 The change to entropy in the Flory-Huggins model is calculated based on the difference in the number of sites available for the polymer chain's center of mass in the pure and mixed phases.
📏 The concept of volume fraction is used instead of mole fraction in the Flory-Huggins Theory to account for the ease of measuring volumes rather than moles.
🔗 The entropy of mixing in the Flory-Huggins model is similar to the ideal solution, but with volume fractions replacing mole fractions.
🔄 The increase in polymer chain length (R) makes the mixing less favorable due to the reduced entropy of mixing, contributing to decreased solubility.
🔄 The Flory-Huggins interaction parameter (χ) is defined as the exchange energy per molecule normalized by thermal energy, indicating the energy cost of mixing unlike molecules.
🌡 The Gibbs free energy equation is used to predict the equilibrium phase behavior of a polymer-solvent mixture, considering both entropy and enthalpy changes.
📈 The total Gibbs free energy expression for the regular solution includes combinatorial entropy and contact dissimilarity terms, which are crucial for understanding phase behavior.
📊 The next class will involve plotting the changes in enthalpy, entropy, and Gibbs free energy to construct phase diagrams, which will help in understanding phase behavior as a function of temperature.

Q & A

What is the main assumption of an ideal solution in terms of molecular size and intermolecular forces?
-An ideal solution assumes that all the molecules of the two components are the same size and that there is no difference in the intermolecular forces between molecules of one interacting with one, one with two, and two with two. This means there is no change in enthalpy when exchanging the nearest neighbors.
Why is the entropy of mixing important in the context of an ideal solution?
-The entropy of mixing is important because it is the only component considered in an ideal solution. It represents the increase in disorder when the components are mixed, and it is the driving force behind the spontaneity of the mixing process in an ideal scenario.
What changes when moving from an ideal solution to a polymer-solvent system?
-When moving from an ideal solution to a polymer-solvent system, two main changes occur: (1) one of the components becomes a polymer, introducing a change to the entropy of mixing, and (2) the introduction of the idea that the intermolecular forces between one and one, and two and two, are different, which can lead to phase separation.
What is the Flory-Huggins Theory and how does it relate to polymer solutions?
-The Flory-Huggins Theory is a model that describes the thermodynamics of mixing polymers with solvents. It takes into account the differences in intermolecular forces and the fact that a polymer chain occupies multiple lattice sites, leading to a different entropy of mixing compared to an ideal solution.
How does the length of a polymer chain (R) affect the entropy of mixing in the Flory-Huggins Theory?
-In the Flory-Huggins Theory, the length of a polymer chain (R) affects the entropy of mixing by reducing the number of possible configurations for the polymer in the mixed phase. As R increases, the volume fraction of the polymer (F2) approaches one, making the entropy of mixing term very small and less favorable, which can lead to phase separation.
What is the significance of the interaction parameter (χ) in the Flory-Huggins Theory?
-The interaction parameter (χ) in the Flory-Huggins Theory represents the extent to which the intermolecular forces between unlike molecules differ from those between like molecules. It is a measure of the unfavorable enthalpy of mixing and is crucial for predicting phase behavior in polymer solutions.
How does the Flory-Huggins Theory account for the enthalpy of mixing in polymer solutions?
-The Flory-Huggins Theory accounts for the enthalpy of mixing by introducing an exchange energy term (ΔW) that represents the difference in interaction energy between unlike molecules (w12) and the average of the interaction energies of like molecules (w11 and w22). This term is used to calculate the change in enthalpy upon mixing.
What is the role of the Gibbs free energy (ΔG) in determining the phase behavior of polymer solutions?
-The Gibbs free energy (ΔG) is used to determine the phase behavior of polymer solutions by considering both the entropy of mixing (favorable) and the enthalpy of mixing (unfavorable). A negative ΔG indicates spontaneous mixing, while a positive ΔG suggests phase separation.
Why do polymers become less soluble as the molecular weight increases according to the Flory-Huggins Theory?
-According to the Flory-Huggins Theory, as the molecular weight of a polymer increases, the entropy of mixing decreases due to the reduced number of configurations available for the polymer in the mixed phase. This makes the mixing less favorable, leading to decreased solubility.
What are block copolymers and how do they relate to phase separation and nanostructures?
-Block copolymers are polymers consisting of two or more covalently linked polymer chains that are chemically different. They can phase separate due to differences in intermolecular forces, but when they do, they can form useful nanostructures with potential applications in microprocessors, filtration membranes, and other technologies.

Outlines

00:00

🔍 Introduction to Ideal and Free Energy in Solutions

The script begins with a review of the concepts of ideal and free energy changes in solutions, focusing on the entropy component due to the assumption of identical molecule sizes and equal intermolecular forces between components. The lecture introduces two developments: considering a polymer as one of the components and acknowledging different intermolecular forces, which can lead to phase separation in polymer solutions. The Flory-Huggins Theory is mentioned as the framework for understanding the entropy of mixing in these systems.

05:10

📚 Transition from Ideal to Regular Solutions with Polymers

This paragraph delves into the transition from ideal to regular solutions, especially when one component is a polymer. It discusses the change in entropy of mixing due to the polymer's size and the assumption that segment size equals solvent size. The concept of volume fraction is introduced to simplify calculations, and the Flory-Huggins Theory's volume fraction-based entropy of mixing is explained, highlighting its relation to the ideal solution case.

10:13

🔗 Entropy Change in Polymer-Solvent Mixing

The script explains the calculation of entropy change during the mixing of polymers and solvents, assuming the same conformational freedom in both pure and mixed phases. It describes the 'quick root' method for estimating entropy change, which involves calculating the difference in available sites for the polymer's center of mass in the pure and mixed states. The paragraph also clarifies the meaning of R, the length of the polymer chain in the model.

15:13

📉 Impact of Polymer Chain Length on Solubility

The lecture discusses how the length of the polymer chain (R) affects solubility, showing that larger R values make mixing less favorable due to the reduced entropy of mixing associated with the polymer component. The connection between the Flory-Huggins entropy of mixing and the ideal solution case is made, with the substitution of mole fractions for volume fractions.

20:15

🔄 Enthalpy of Mixing in Polymer Solutions

This section introduces the enthalpy of mixing, which is no longer zero due to the presence of different intermolecular forces between unlike molecules. It outlines the calculation of enthalpy change, considering the pairwise interactions between molecules and the energy associated with these interactions, known as the interaction energies w11, w12, and w22.

25:15

🔗 Vander Waals Forces and Their Impact on Mixing

The script explores the types of Vander Waals forces, including dipole-dipole, dipole-induced dipole, and London dispersion forces, and their role in the enthalpy of mixing. It emphasizes that hydrogen bonding is a strong case of dipole-dipole interaction and discusses the general attractive nature of these forces, which are crucial for understanding the enthalpy changes in mixing.

30:19

📊 Calculating Enthalpy of Mixing with Interaction Energies

The paragraph focuses on the calculation of the enthalpy of mixing by considering the interaction energies between like and unlike molecules. It introduces the concept of exchange energy and the interaction parameter, which quantifies the energy penalty for mixing unlike molecules. The algebraic simplification to derive the final expression for the enthalpy of mixing is briefly mentioned.

35:22

🌡 Effect of Interaction Parameter on Free Energy and Mixing

This section explains the role of the interaction parameter (Kai) in determining the spontaneity of mixing. It shows that a positive Kai value leads to an unfavorable enthalpy of mixing, which opposes spontaneous mixing. The final expression for the Gibbs free energy of mixing is presented, incorporating both entropy and enthalpy contributions.

40:26

🧩 Phase Behavior Predictions Using Free Energy

The script concludes with a discussion on using the derived expressions for entropy, enthalpy, and free energy to predict phase behavior in polymer-solvent systems. It mentions the upcoming task of plotting these quantities and constructing phase diagrams to understand the conditions for one-phase or two-phase behavior.

45:28

📈 Future Outlook on Polymer Mixing and Phase Segregation

The final paragraph provides an outlook on the next steps of the lecture series, which will involve plotting the mixing energies and constructing phase diagrams. It also touches on the general incompatibility of polymers due to unfavorable enthalpy of mixing and the exceptions to this rule, such as block copolymers, which can form useful nanostructures.

Mindmap

Keywords

💡Ideal Solution

An 'Ideal Solution' is a theoretical construct in thermodynamics where the mixing of two or more components occurs without any change in enthalpy due to the assumption of identical molecular sizes and intermolecular forces. In the video, the concept is introduced as a baseline for understanding more complex solutions, particularly when moving from simple solvents to polymers and considering the effects of different intermolecular forces.

💡Entropy

Entropy is a thermodynamic property that measures the degree of disorder or randomness in a system. In the context of the video, it is a key component in understanding the mixing of ideal solutions, where the change in entropy is solely due to the increased randomness when different components are mixed. The script discusses how the entropy of mixing is calculated and how it changes when considering polymers.

💡Flory-Huggins Theory

The Flory-Huggins Theory is a model used to describe the thermodynamic properties of polymer solutions. It extends the concept of an ideal solution to include the effects of different intermolecular forces and the size of polymer chains. The theory is central to the video's discussion on how the introduction of polymers changes the entropy and enthalpy calculations for solution mixing.

💡Polymer

A 'Polymer' is a large molecule composed of repeating structural units, typically the basis of plastics and other materials. In the script, polymers are used to illustrate how the presence of a component with a high molecular weight affects the thermodynamics of a solution, leading to different entropy and enthalpy changes compared to solutions of smaller molecules.

💡Molar Volume

Molar volume refers to the volume occupied by one mole of a substance. In the video, the molar volume of the polymer is contrasted with that of the solvent to define the relationship between the size of the polymer chains and the solvent molecules, which is crucial for the Flory-Huggins Theory.

💡Volume Fraction

Volume fraction is the ratio of the volume of a component to the total volume of the mixture. The script transitions from mole fraction to volume fraction in the context of the Flory-Huggins Theory to simplify the calculation of entropy changes in polymer solutions, as it is often easier to measure volumes rather than moles.

💡Intermolecular Forces

Intermolecular forces are the forces of attraction or repulsion that act between neighboring molecules. The video discusses how different intermolecular forces between unlike molecules can lead to a non-zero enthalpy change upon mixing, which is a departure from the ideal solution model.

💡Vander Waals Forces

Vander Waals Forces are weak intermolecular forces that include dipole-dipole interactions, dipole-induced dipole interactions, and London dispersion forces. The script explains these forces as the underlying causes of the enthalpy changes in non-ideal solutions, particularly when different types of molecules are mixed.

💡Hydrogen Bonding

Hydrogen bonding is a particularly strong type of dipole-dipole interaction that occurs when a hydrogen atom covalently bonded to a highly electronegative atom interacts with another electronegative atom. The video script mentions hydrogen bonding as a special case of Vander Waals Forces, highlighting its significance in the context of intermolecular forces.

💡Phase Separation

Phase separation refers to the process where two or more distinct phases emerge from a mixture due to differences in solubility or intermolecular forces. The script discusses phase separation in the context of polymer solutions, explaining how differences in intermolecular forces can lead to the separation of phases.

💡Gibbs Free Energy

Gibbs Free Energy is the maximum reversible work that a thermodynamic system can perform at constant temperature and pressure. In the script, the Gibbs Free Energy equation is used to relate the enthalpy and entropy changes to the spontaneity of mixing in polymer solutions, providing a comprehensive view of the thermodynamics involved.

Highlights

Introduction to the derivation of expressions for ideal change and free energy of an ideal solution, emphasizing the assumptions of identical molecular sizes and indistinguishable intermolecular forces.

Transition from an ideal solution to a regular solution model, incorporating a polymer component and unequal intermolecular forces.

Explanation of the Flory-Huggins Theory, which accounts for the entropy of mixing in polymer solutions and the impact of different interaction energies.

Development of the entropy term in the Flory-Huggins Theory, using a lattice model to represent polymer chains and solvents.

Discussion on the concept of volume fraction and its importance in the Flory-Huggins Theory, as opposed to mole fraction.

Calculation of the change in entropy upon mixing, based on the difference in available sites for the polymer chain's center of mass.

Recovery of the ideal solution theory as a special case of the Flory-Huggins Theory when R equals 1, simplifying the model to monomers.

Introduction of the enthalpy of mixing, which is no longer zero due to the consideration of unequal intermolecular forces between different molecules.

Explanation of van der Waals forces, including dipole-dipole, dipole-induced dipole, and London dispersion forces, and their role in mixing enthalpy.

Derivation of the enthalpy of mixing expression, considering the exchange energy and the probability of unlike molecule interactions.

Introduction of the Flory-Huggins interaction parameter, χ, which quantifies the unfavorable mixing due to different intermolecular forces.

Expression of the Gibbs free energy for a regular solution, incorporating both entropy and enthalpy terms, and its implications for phase behavior.

Insight into the reduced solubility of polymers with increasing molecular weight, as explained by the Flory-Huggins Theory.

Discussion on the challenges of mixing two different polymers, highlighting the general avoidance of mixing due to unfavorable enthalpy.

Mention of block copolymers as an exception to the rule of polymer immiscibility, and their unique properties and applications.

Preview of the next class's focus on plotting the mixing properties and constructing phase diagrams to understand phase behavior as a function of temperature.

Transcripts

Browse More Related Video

Ep13 Cloud point and phase diagrams - UC San Diego - NANO 134 Darren Lipomi

Ep14 solubility parameters and gel permeation chromatography - UC San Diego - NANO 134 Darren Lipomi

Polymer Science and Processing 01: Introduction

AP Chemistry Unit 3 Review: Intermolecular Forces and Properties

Introduction to Materials Engineering: CH9

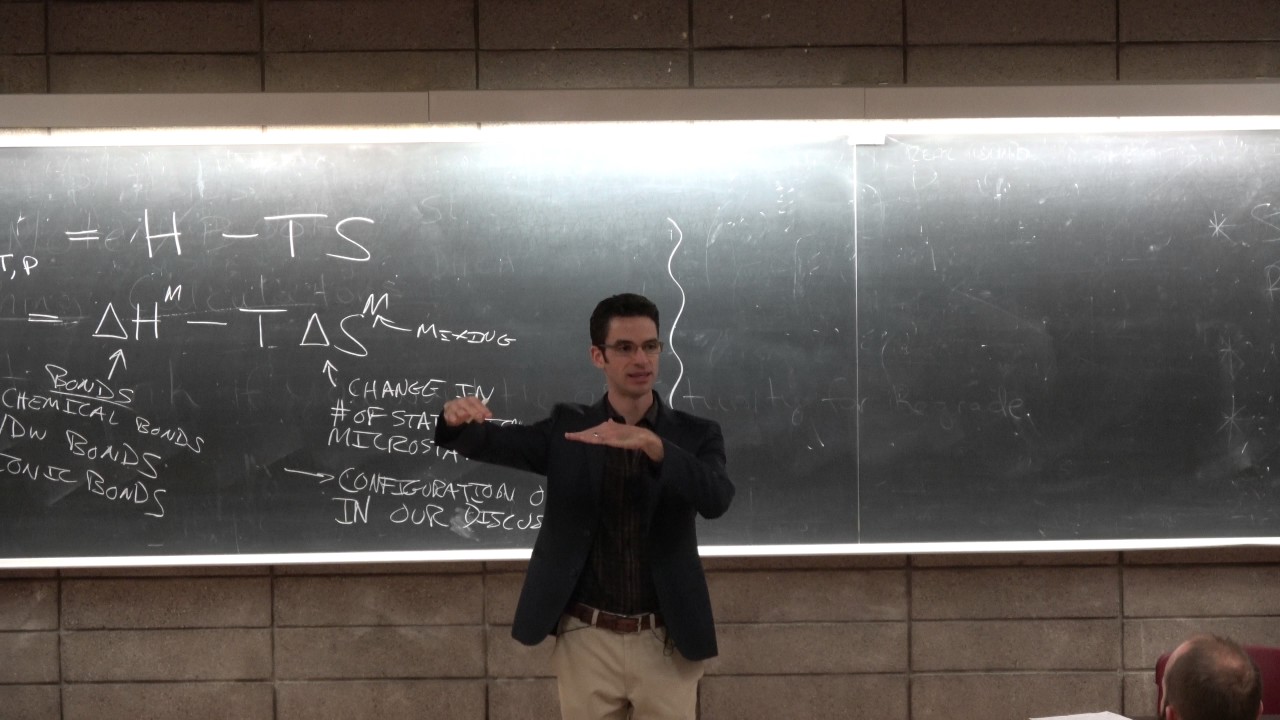
Ep11 Thermodynamics, ideal solutions, entropy - UC San Diego - NANO 134 Darren Lipomi

Related Tags

Polymer Science Phase Separation Flory-Huggins Entropy Mixing Enthalpy Change Intermolecular Forces Solution Theory Polymer Solubility Mixing Entropy Chemical Equilibrium