Chaos Equations - Simple Mathematical Art
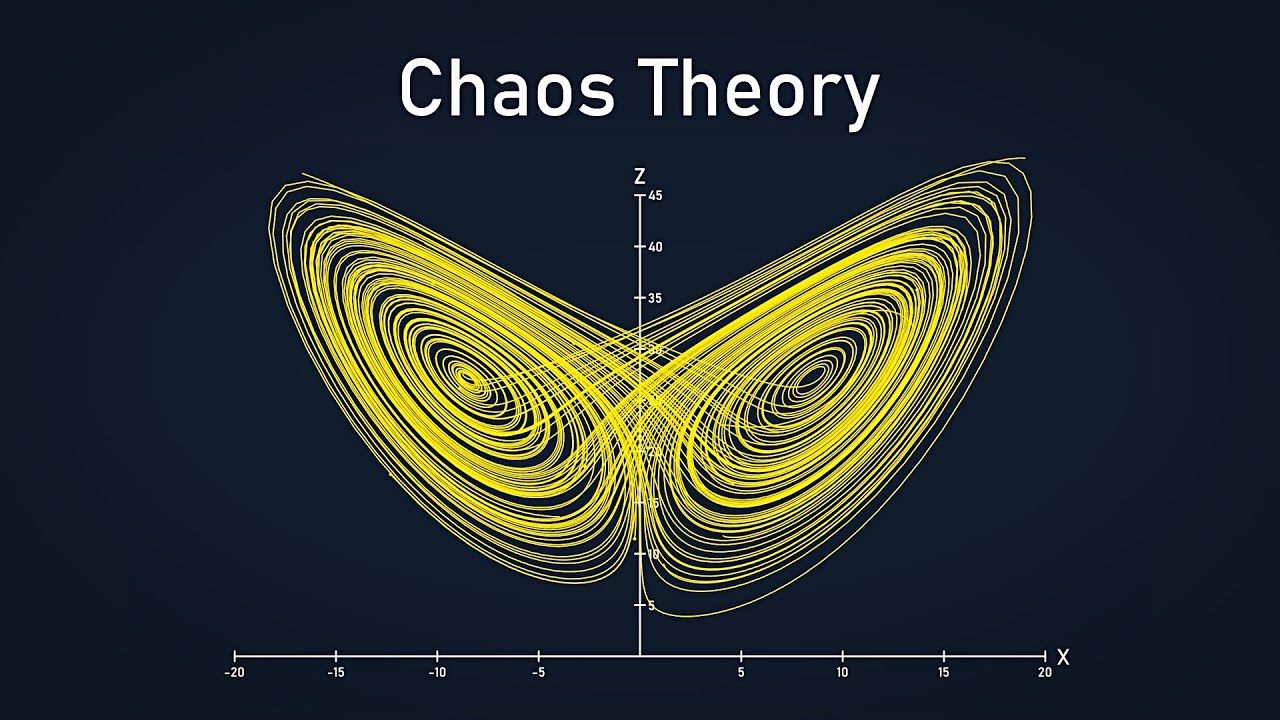
TLDRThe video script introduces a fascinating concept known as 'chaos equations,' which are dynamic systems that evolve over time. These mathematical art pieces are created using simple middle school-level math, without the need for complex concepts like imaginary numbers. The process involves starting with a point, represented by the variable T, and applying random equations to update the point's coordinates. Each updated point is then drawn on screen in a unique color, and the process repeats, creating an ever-changing visual display. The video showcases some of the creator's favorite chaos equation animations, complete with artistic trails and dynamic speed adjustments. The creator also provides a code feature for saving and sharing favorite equations, and offers the program and source code for download. While the creator's younger self discovered this independently, they acknowledge that these chaos equations might have a more formal name, but they liken it to a discrete version of a strange attractor and the flame fractals from Electric Sheep.
Takeaways
- 🎨 The speaker discusses creating mathematical art using what they term 'chaos equations', which are visually appealing and simple to understand.
- 🔍 These chaos equations are based on dynamic systems that evolve over time, represented by the variable T.
- ⏰ Time plays a crucial role in the art, with the value of T starting low and increasing as the animation progresses.
- 📍 The process begins with a point whose coordinates are initialized to T, and an equation is applied to update the point's position.
- 🌈 Unique colors are used to draw each point on the screen, contributing to the visual complexity of the art.
- 🔧 The program uses random equations to update points, and surprisingly, most of these random equations result in aesthetically pleasing patterns.
- 📈 The artist added features like trails and dynamic speed changes to enhance the visual interest of the art.
- 🎵 The script includes a musical component, with the speaker sharing some of their favorite creations set to music.
- 💾 The audience is encouraged to download the program or source code to try creating their own mathematical art.
- 🔗 A six-letter code system is provided to easily save and share favorite equations for the mathematical art.
- 🧐 The speaker acknowledges that while they independently discovered this technique, it may have a formal mathematical name they are unaware of.
- 🔬 The chaos equations are compared to a discrete version of a strange attractor and are reminiscent of the flame fractals used in Electric Sheep, though distinct.
Q & A
What are chaos equations as described in the transcript?
-Chaos equations, as described, are a form of mathematical art created using dynamic systems that change over time. They are generated by starting with a point and applying a simple equation to update its coordinates, then drawing the point on the screen with a unique color. The process is repeated with time represented by the variable T, which increases as the animation progresses.
What level of math is required to understand chaos equations?
-No more than middle school math is required to understand chaos equations, as they do not involve imaginary numbers or other complicated concepts.
How does the time variable T function in the chaos equations?
-In chaos equations, time is represented by the variable T, which starts at a low value and slowly increases as the animation progresses. It is used to initialize the coordinates of the starting point and is updated with each time step.
What is the process for creating a new point in the chaos equation animation?
-A new point is created by starting with a point whose coordinates are initialized to the current value of T. An equation is then applied to update the point's coordinates. The updated point is drawn to the screen with a unique color, and the process is repeated with the new point.
How does the appearance of the chaos equation animation change over time?
-As time changes, represented by the increasing value of T, the points in the chaos equation animation also change. This results in a dynamic and evolving visual pattern.
What additional features were added to enhance the chaos equation animation?
-Fancy trails and dynamic speed changes were added to the chaos equation animation. The speed of the animation is adjusted to speed up when nothing interesting is happening, creating a more engaging visual experience.
How can viewers save and share their favorite chaos equation animations?
-The creator has provided a feature that allows viewers to save and load equations using six-letter codes. This makes it easy for viewers to capture and share their favorite creations or interesting patterns they discover.
Is there a formal mathematical name for the chaos equations presented?
-The creator is unsure if chaos equations have a more formal mathematical name, as they were independently discovered and do not seem to be widely recognized under that specific term.
How do chaos equations relate to other mathematical concepts?
-Chaos equations are a discrete version of a strange attractor and are reminiscent of the flame fractals used in the Electric Sheep project, although they are not identical to that algorithm.
What is the purpose of the six-letter code system in the chaos equation program?
-The six-letter code system simplifies the process of saving and sharing specific chaos equation configurations, allowing users to easily document and communicate their favorite or discovered patterns.
How can one obtain the program or source code for creating chaos equation animations?
-The program or source code can be downloaded from the description provided by the creator, allowing interested individuals to try out and experiment with creating their own chaos equation animations.
What is the significance of the unique color assigned to each point in the chaos equation animation?
-Assigning a unique color to each point helps to distinguish the individual points and contributes to the overall aesthetic of the animation, making the evolving patterns more visually appealing.
What is the role of randomness in the chaos equation animations?
-Randomness is used to select different equations for updating the points' coordinates, which contributes to the unpredictability and variety of the resulting patterns, making each animation unique.
Outlines
🎨 Chaos Equations in Mathematical Art
The speaker introduces the concept of 'chaos equations' in the context of mathematical art. They recount finding old GameMaker projects and being inspired to create a new, polished version of these dynamic systems. The art is created using simple math, with no need for complex concepts like imaginary numbers. The process involves starting with a point at a low value of time variable T and applying random equations to update the point's coordinates. The updated points are then drawn on the screen in a unique color, with the process repeated to create a changing pattern over time. The speaker also mentions adding visual effects like trails and varying the animation speed. They share some of their favorite creations and provide a method for saving and loading preferred equations using six-letter codes. The video concludes with an invitation for viewers to download the program, try it out, and share their creations. The speaker also notes the possibility of these chaos equations having a more formal name, as they are similar to discrete strange attractors and flame fractals.
Mindmap
Keywords
💡Chaos Equations
💡GameMaker
💡Dynamic Systems
💡Variable T
💡Middle School Math
💡Random Equations
💡Unique Color
💡Fancy Trails
💡Speed Control
💡Six Letter Codes
💡Strange Attractor
💡Electric Sheep
Highlights
The creator discusses chaos equations, a mathematical art form, which can be understood with middle school math.
Chaos equations are dynamic systems that evolve over time, represented by the variable T.
The process involves starting with a point and applying an equation to update its coordinates.
Random equations are used in the program, with most producing visually appealing results.
Each updated point is drawn on the screen with a unique color.
The animation speeds up when no interesting changes are occurring.
The creator adds fancy trails and dynamic speed changes for visual enhancement.
A six-letter code system is provided to easily save and share preferred equations.
The program or source code is available for download to allow others to experiment.
The creator acknowledges that chaos equations may have a more formal name but was unable to find one.
The art form is a discrete version of a strange attractor, similar to but distinct from flame fractals.
The creator invites viewers to try the program and share their creations.
The transcript includes a disclaimer about the independent discovery of chaos equations.
The creator expresses enthusiasm to see what others will make using the chaos equations.
Music is used throughout the presentation to enhance the viewing experience.
The creator shares some of their favorite chaos equation animations.
The simplicity of the chaos equations allows for a wide range of creative possibilities.
The creator emphasizes the ease of understanding and applying chaos equations due to their straightforward nature.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: