Business Calculus - Math 1329 - Section 2.6 - Implicit Differentiation and Related Rates
TLDRThe video script is an educational walkthrough of implicit differentiation, related rates, and their applications in calculus. It begins with an explanation of implicit differentiation, which is used to find the derivative of an equation not explicitly solved for y. The process is illustrated with examples, including finding the derivative of a cubed function and the equation of a circle, and determining the slope of the tangent line at a specific point on the circle. The script then delves into related rates, which involve differentiating equations with respect to time to find how one variable changes in relation to another. Examples provided include the rate of change of a square's area as its sides increase and the rate at which the radius of an oil slick expands. The video concludes with a problem involving the supply and price of dog collars, demonstrating how to use implicit differentiation to solve for the rate of change in supply. The script is a comprehensive guide for students learning to apply calculus to real-world problems.
Takeaways
- 📘 Implicit differentiation is used when an equation involves y's and x's but isn't solved for y, allowing us to find the derivative of y with respect to x.
- 🔑 The chain rule is fundamental in implicit differentiation, as it accounts for the rate of change of y in relation to x.
- 🧮 When differentiating y in an implicit context, we multiply by dy/dx to represent the rate of change of y with respect to x.
- ✍️ The derivative of an implicit equation is a function of both x and y, which may require both coordinates to evaluate the derivative at a point.
- 📐 For finding the equation of a tangent line to a curve at a given point, we first find the slope of the tangent line using implicit differentiation.
- 🟡 The slope of the tangent line to a circle at a specific point can be found by differentiating the circle's equation and then evaluating at that point.
- 📊 To solve related rates problems, we follow a systematic approach: read the question, draw a picture, create variables, form equations, differentiate implicitly with respect to time, substitute known values, and solve for the desired rate.
- 🌟 In related rates problems, the rate of change of one variable can be determined by differentiating the given equation with respect to time, even if time is not explicitly present in the equation.
- 🛑 The area of a shape like a square or circle is not changing at a constant rate; it depends on the current dimensions and their rates of change.
- 🚰 For a related rates problem involving a volume, such as an oil slick, we consider the shape's geometry (like a cylinder) and use the formula for volume to find the rate of change of dimensions.
- 📈 When the price of an item changes over time, the rate of change in supply can be found by differentiating the supply equation with respect to time and solving for the rate of change in supply.
Q & A
What is the purpose of implicit differentiation?
-Implicit differentiation is used when you have an equation with variables y and x, but the equation is not explicitly solved for y. It allows you to take the derivative of y with respect to x, which is useful for finding slopes of tangent lines and rates of change without explicitly isolating y.
How does the chain rule apply to implicit differentiation?
-The chain rule is applied in implicit differentiation by multiplying the derivative of y by the derivative of y with respect to x (dy/dx), as y is considered a function of x even if it's not explicitly written as such.
In the given script, what is the derivative of y^3 + x^2 = 3x with respect to x?
-The derivative with respect to x is given by 3y^2 * (dy/dx) + 2x = 3. After solving for dy/dx, we get dy/dx = (3 - 2x) / (3y^2).
What is the equation of the tangent line to a circle with radius 5 at the point (3, 4)?
-The equation of the tangent line at the point (3, 4) on the circle x^2 + y^2 = 25 is y = -3/4 * x + 25/4.
How is the slope of the tangent line to the circle found?
-The slope of the tangent line is found by implicitly differentiating the equation of the circle with respect to x, then using the slope formula (-x/y) at the given point (3, 4), which results in a slope of -3/4.
What is the slope of the tangent line to the curve 3x/(x + y^2) = 9 at the point (-6, -2)?
-The slope of the tangent line at the point (-6, -2) is found by differentiating the given equation and plugging in the coordinates, which results in a slope of 1/6.
What is the product rule used for in calculus?
-The product rule is used in calculus to find the derivative of a product of two functions. It states that the derivative of the product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
How do you find the slope of the tangent line to the curve y * sqrt(x^2 + y^2) = 65 at the point (12, 5)?
-You first apply the product rule to differentiate the given equation, then plug in the coordinates (12, 5) into the derivative to solve for dy/dx, which gives the slope of the tangent line.
What are the steps to solve related rates problems?
-The steps to solve related rates problems are: 1) Read the question, 2) Draw a picture if applicable, 3) Create your variables and describe them, 4) Write the equation(s) needed for the problem, 5) Differentiate implicitly with respect to time, 6) Substitute values for the regular and rate variables, and 7) Solve for the variable you need.
How is the area of a square related to the rate at which its sides are increasing?
-The area of a square (A) is related to the side length (s) by A = s^2. The rate at which the area is changing (dA/dt) is related to the rate at which the side length is changing (ds/dt) by the equation dA/dt = 2s * ds/dt.
What is the volume formula for a cylinder with a changing radius but constant thickness?
-The volume formula for a cylinder with a constant thickness (h) and a changing radius (r) is V = (pi * r^2 * h). If h is constant, it can be taken out of the derivative when finding the rate of change of volume with respect to time.
How is the supply function related to the price of dog collars in the given economic model?
-The supply function is related to the price of dog collars by the equation x^2 - 8x * sqrt(p) - 2p^2 = 48, where x is the supply in hundreds of collars and p is the price in dollars per collar. The rate of change of supply with respect to price can be found by differentiating this equation with respect to time.
Outlines
📚 Implicit Differentiation Basics
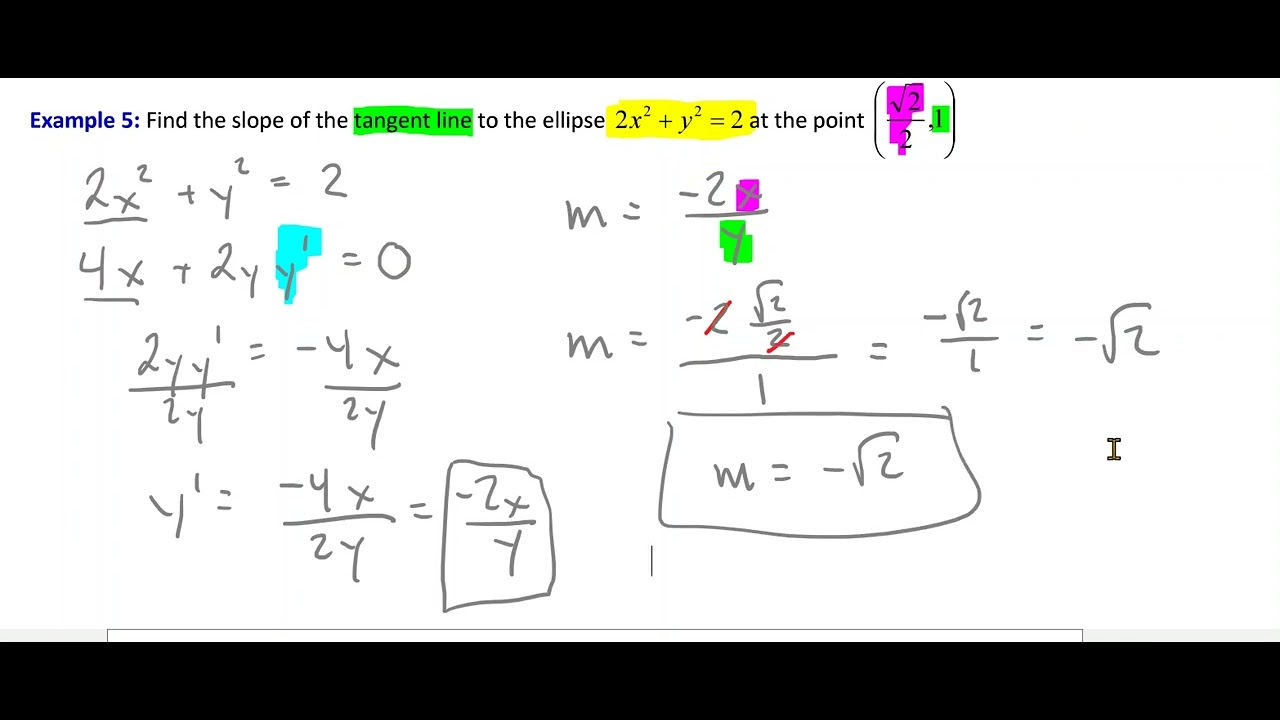
This paragraph introduces implicit differentiation, a technique used when an equation involves both y and x but isn't explicitly solved for y. It explains the process of differentiating with respect to x, using the chain rule to account for y as a function of x. An example problem is presented where the derivative of y cubed plus x squared equal to 3x is solved, resulting in a formula for dy/dx that depends on both x and y.
🔍 Finding Tangent Lines to Curves
The second paragraph delves into finding the equation of a line tangent to a curve at a specific point. Using the circle equation x^2 + y^2 = 25 and a given point on the circle, the derivative is taken implicitly to find the slope of the tangent line. The process involves solving for dy/dx and applying it to find the slope at the given point, which is then used to derive the equation of the tangent line.
📐 Derivatives and Tangent Lines in Various Forms
The third paragraph explores finding the slope of the tangent line to different forms of equations, such as 3x/(x + y^2) = 9, at specific points. It demonstrates the use of the quotient rule for differentiation and how to apply the derived formula at a given point to find the slope of the tangent line.
🔢 Product Rule and Tangent Line Calculations
The fourth paragraph discusses the use of the product rule for derivatives when dealing with equations involving products, such as y times the square root of x^2 + y^2 = 65. It outlines the steps to find the derivative, simplify the equation, and then plug in values to solve for dy/dx at a given point, which represents the slope of the tangent line.
🔄 Related Rates: Understanding Rate Changes
This paragraph introduces related rates problems, which involve determining how one quantity changes in relation to another. It provides a step-by-step method for solving these problems, including reading the question, drawing a picture, creating and describing variables, differentiating with respect to time, substituting known values, and solving for the required variable. An example involving the area of a square with increasing sides is used to illustrate the process.
🌊 Modeling Real-World Scenarios with Related Rates
The sixth paragraph applies related rates to a real-world scenario of an oil spill on the ocean, forming a circular oil slick. It guides through setting up variables for radius, thickness, and volume, and their respective rates of change. The problem involves finding the rate of change of the radius when the slick has a certain radius and thickness, using the volume formula for a cylinder and differentiating with respect to time.
📈 Supply and Demand Functions with Related Rates
The seventh paragraph presents a related rates problem involving the supply and price of dog collars. It outlines the steps to declare variables, use the given equation to find the supply based on price, differentiate with respect to time, and solve for the rate of change in supply. The problem requires finding the rate at which supply changes when the price is increasing at a given rate.
🧮 Solving for Rate of Change in Supply
The final paragraph concludes the related rates problem by solving for the rate of change in supply when the price is $4 per collar and increasing at a specific rate. It involves substituting known values into the differentiated equation, solving for the unknown supply rate, and interpreting the result in the context of the problem.
Mindmap
Keywords
💡Implicit Differentiation
💡Derivative
💡Chain Rule
💡Related Rates
💡Slope of Tangent Line
💡Quotient Rule
💡Product Rule
💡Rate Variables
💡Differential Equations
💡Chain Rule
💡Rate of Change
Highlights
Implicit differentiation is required when an equation involves y's and x's but is not solved for y.
The process involves taking the derivative of y with respect to x, considering y as a function of x.
Chain rule is applied when differentiating y, resulting in multiplying by dy/dx.
Example 1 demonstrates finding the derivative dy/dx of the equation y^3 + x^2 = 3x.
For a circle with equation x^2 + y^2 = 25, the slope of the tangent line at point (3,4) is derived.
The equation of the tangent line to a circle at a given point is found using the slope and point.
Example 3 involves using the quotient rule to find the slope of the tangent line to the curve 3x/(x + y^2) = 9 at point (-6, -2).
Product rule is used in Example 4 to find the slope of the tangent line to y * sqrt(x^2 + y^2) = 65 at (12, 5).
Related rates involve differentiating with respect to time, t, to find rates of change.
A method for solving related rate problems is outlined, including reading the question, drawing a picture, creating variables, differentiating, and solving.
Example 5 involves a square with sides increasing at 3 cm/s, and finding how fast the area changes when the sides are 10 cm.
The volume of a cylinder, representing an oil slick, is used to find how fast the radius changes given a constant thickness and flow rate.
Example 7 deals with the supply and price relationship of dog collars, finding how fast the supply changes with a given price increase.
The importance of units in related rate problems is emphasized, ensuring that the units make sense in the context of the problem.
The transcript provides a step-by-step guide to solving calculus problems involving implicit differentiation and related rates.
Real-world applications such as oil spills and market supply are used to demonstrate the practical use of calculus concepts.
The process of solving for dy/dx in various scenarios is detailed, showing the application of the chain rule and other calculus principles.
The transcript concludes with a comprehensive approach to solving related rate problems, emphasizing the importance of a systematic method.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: