Infinite Series Multiple Choice Practice for Calc BC (Part 6)

turksvids
14 Apr 202215:42
EducationalLearning
32 Likes 10 Comments

TLDRThis video script is part of a series focused on preparing for the BC Calculus exam, specifically delving into series and multiple-choice questions. The presenter covers various tests to determine the convergence or divergence of infinite series, including the Integral Test, nth Term Test, and Ratio Test. The Integral Test is demonstrated with an example series, leading to its convergence. The nth Term Test is applied to several series, identifying conditions under which it can determine divergence. The Ratio Test is also explored, with the presenter discussing its application and limitations. The video concludes with a look at a specific series where the sum equals five, and the implications for the nth term limit. Throughout, the presenter emphasizes the importance of understanding limits and their role in series convergence or divergence, providing clear explanations and examples to aid comprehension.

Takeaways
  • 📚 The integral test is used to determine the convergence of series where the function is positive, continuous, and decreasing from 1 to infinity.
  • 🔢 For the nth term test, taking the limit as n approaches infinity is crucial. If the limit is not zero, the series diverges.
  • ∫ When applying the integral test, it's important to set up the integral correctly and use the limit as the upper bound approaches infinity.
  • 📉 The cosine function does not have a limit as its argument approaches infinity, which can indicate divergence of the related series.
  • 🌟 If a series converges, the limit of the nth term must be zero. However, a limit of zero does not guarantee convergence.
  • 🤔 The ratio test is a common method to determine series convergence or divergence by comparing the ratio of consecutive terms.
  • 📈 Exponential functions tend to dominate polynomials as n approaches infinity, which can help predict the convergence of a series.
  • 📌 The ratio test can be inconclusive for p-series (series involving a power of n) since the test always results in 1.
  • 🚫 A limit of a series term that does not approach zero indicates divergence, as seen with the nth term test and ratio test applications.
  • 🔑 The series \( \sum_{n=1}^{\infty} a_n \) converges if \( \lim_{n \to \infty} a_n = 0 \), but this condition alone is not sufficient to confirm convergence.
  • 📦 The summation of a constant series \( \sum_{n=1}^{\infty} 1 \) equals the number of terms, which in this case is \( n \).
Q & A

  • What is the Integral Test used for in the context of the video?

    -The Integral Test is used to determine the convergence of an infinite series. It is applicable when the series is positive, continuous, and decreasing from a certain point to infinity.

  • How does the video demonstrate the use of the Integral Test?

    -The video demonstrates the Integral Test by setting up an integral with an upper bound 'b' and taking the limit as 'b' approaches infinity. It uses 'u' substitution to evaluate the integral and determine the convergence of the series.

  • What is the nth Term Test used for in the video?

    -The nth Term Test is used to determine the divergence of a series. It involves taking the limit of the nth term of the series as 'n' approaches infinity.

  • How does the video handle the case when the limit of the nth term test is zero?

    -If the limit of the nth term test is zero, the test does not provide information about the convergence or divergence of the series. It is not sufficient to conclude that the series converges.

  • What does the video say about the relationship between the limit of the nth term and the convergence of a series?

    -The video explains that if a series converges, then the limit of the nth term must be zero. However, the converse is not necessarily true; a limit of zero does not guarantee convergence.

  • How does the video approach the problem of determining which series diverge?

    -The video approaches this by applying the nth Term Test to each series and checking if the limit as 'n' approaches infinity is not zero, which would indicate divergence.

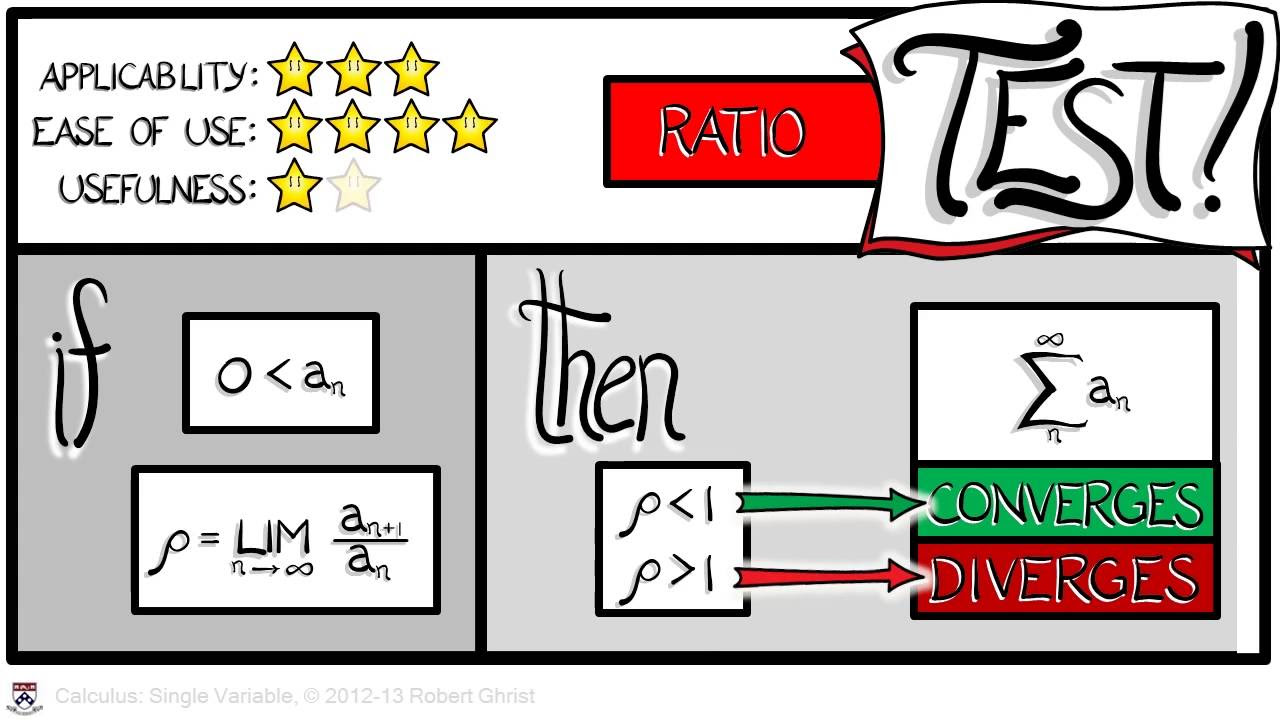
  • What is the Ratio Test mentioned in the video used for?

    -The Ratio Test is used to determine the convergence or divergence of an infinite series. It involves finding the limit of the ratio of consecutive terms of the series as 'n' approaches infinity.

  • How does the video apply the Ratio Test to a series involving powers of 'n'?

    -The video applies the Ratio Test by dividing the (n+1)th term by the nth term of the series, simplifying the expression, and then taking the limit as 'n' approaches infinity to see if it is less than one.

  • What is the significance of the limit being less than one in the Ratio Test?

    -If the limit obtained from the Ratio Test is less than one, it implies that the series converges. If the limit is greater than or equal to one, the test is inconclusive or indicates divergence.

  • How does the video handle a series where the limit of the Ratio Test is exactly one?

    -When the limit of the Ratio Test is exactly one, the test is inconclusive, and the series could either converge or diverge. Additional tests or methods are needed to determine the behavior of the series.

  • What is the summation series mentioned at the end of the video?

    -The summation series mentioned at the end of the video is the sum from 1 to infinity of a constant term 'a_sub_n' which is equal to one for all positive integers 'n'. This series is a well-known arithmetic series that sums to 'n'.

  • What is the final advice given by the video for students preparing for the BC Calculus exam?

    -The video advises students to practice a variety of series convergence and divergence tests, including the Integral Test, nth Term Test, and Ratio Test, and to understand the implications of the limits obtained from these tests for the behavior of the series.

Outlines
00:00
📚 Introduction to Series Multiple Choice Questions

This paragraph introduces the video's focus on series multiple-choice questions for the BC calculus exam. It is part six of a series, with parts one through five already available and the expectation that eight parts will be completed. The integral test is discussed as a method to determine the convergence of the infinite series e^(1/n) / n^2, with an explanation of the process to set up and evaluate the integral, including the use of limits and u-substitution. The video also covers the nth term test for divergence and provides examples of how it is applied to different series.

05:02
🔍 Applying the Ratio and nth Term Tests

The paragraph delves into the application of the ratio test and nth term test to determine the convergence or divergence of various series. It discusses the importance of limits in these tests and provides examples of how to apply them to geometric and p-series. The speaker also touches on the concept of the limit of a series being zero as a condition for convergence and how the ratio test can be inconclusive for p-series. The paragraph concludes with a specific problem about the sum of a series being equal to five and what that implies for the limit of the series' terms.

10:02
🤔 Ratio Test for Series Convergence

This section of the script focuses on the ratio test and its application to determine the convergence of a series. The speaker discusses the process of setting up the ratio test for a given series and how to interpret the results. The paragraph includes examples of applying the ratio test to different series, including one involving the natural number n and the function n^p / 4^n, where p is a positive value. The speaker asserts that any positive value of p will result in the series converging, and provides reasoning using the ratio test.

15:03
🌟 Summation of a Constant Series

The final paragraph discusses a specific summation series where the term a_n is equal to one for all positive integers. The speaker explains that the nth partial sum of this series, denoted as s_n, is simply equal to n. This is demonstrated through a few examples, showing that the sum from one to n equals n. The speaker also mentions the relevance of this summation in the context of Riemann sums and definite integrals, which are topics covered in their classes.

Mindmap
Keywords
💡Integral Test
The Integral Test is a method used to determine the convergence or divergence of an infinite series by comparing it to an improper integral. In the video, it is used to assess the series involving e^(1/n)/n^2, where the presenter sets up an integral from 1 to infinity and applies the limit as the upper bound approaches infinity to conclude that the series converges.
💡nth Term Test
The nth Term Test, also known as the Divergence Test, involves taking the limit of the series' nth term as n approaches infinity. If the limit is not zero, the series diverges. In the video, this test is applied to several series to determine if they diverge, such as the series involving natural logarithms and alternating series.
💡Convergence
Convergence in the context of series refers to the approach of the sum of an infinite series to a finite value. The video discusses various tests, like the Integral Test and nth Term Test, to determine if a series converges. For instance, the series involving e^(1/n)/n^2 is shown to converge using the Integral Test.
💡Divergence
Divergence, the opposite of convergence, occurs when the sum of an infinite series does not approach a finite value but instead grows without bound. The video script discusses using the nth Term Test to identify divergence in series, such as the series involving k/(2k+1) and k^2/(n^2).
💡Ratio Test
The Ratio Test is a criterion used to determine the convergence or divergence of a series. It involves comparing the limit of the ratio of consecutive terms as n approaches infinity to the value 1. If the limit is less than 1, the series converges; if greater than 1, it diverges. In the video, the Ratio Test is applied to series involving powers of pi and exponential functions.
💡Geometric Series
A geometric series is a type of series where each term is a constant multiple of the previous term. The video mentions geometric series in the context of discussing series that could potentially converge or diverge based on the value of their common ratio. An example given is n/4^n, which definitely converges.
💡p-Series
A p-series is a special type of series of the form 1/n^p, where p is a real number. The video discusses p-series in the context of the Ratio Test, noting that applying the Ratio Test to a p-series always results in an inconclusive answer of 1, thus not helping to determine convergence or divergence.
💡Limit
In calculus, a limit is the value that a function or sequence approaches as the input approaches some value. The video frequently uses limits, particularly as n approaches infinity, to apply various convergence tests to infinite series and determine their behavior.
💡Summation
Summation, often represented by the sigma symbol (∑), is the operation of adding a sequence of numbers. The video refers to the summation when discussing the partial sums of a series, such as the series where each term is 1, leading to a sum that equals the number of terms, n.
💡Riemann Sums
Riemann Sums are a method used to approximate the area under a curve, which can be used to approximate definite integrals. The video script mentions Riemann sums in the context of converting them into definite integrals and taking limits, which is a technique used in calculus to deal with infinite series.
💡Partial Sum
A partial sum of a series is the sum of the first n terms of the series. In the video, the presenter calculates the nth partial sum for a series where each term is 1, showing that the partial sum is simply equal to n, the number of terms added.
Highlights

The video is part of a series focusing on multiple-choice questions for the BC Calculus exam.

The Integral Test is introduced to determine the convergence of an infinite series involving e^(1/n)/n^2.

The series is shown to be positive, continuous, and decreasing, which is a prerequisite for using the Integral Test.

The limit as b approaches infinity of the integral from 1 to b of 1/x^2 * e^(1/x) is computed.

The result of the integral test shows the series converges, with the answer being A.

The nth Term Test is used to determine divergence for different series, with limits evaluated as n approaches infinity.

For series involving ln(n), k/(2k+1), and k^2/(2k+1), the limits are evaluated to determine divergence.

It is noted that if the limit of the absolute value is not zero, the series diverges.

The series involving cosine of pi/n is shown to diverge by the nth Term Test, with the limit being cos(0) which is 1.

All options in a question about series divergence are found to diverge by the nth Term Test.

A series with a sum of 5 and positive terms is explored, with the limit of the nth term approaching zero being a requirement for convergence.

The Ratio Test is applied to a series involving n*pi^(2n)/17^n to determine convergence, resulting in an inequality.

The question asks for the positive values of p for which the series n^p/4^n converges, with the suggestion that any p > 0 may suffice.

The Ratio Test is used to evaluate the series (n+1)*pi^(2(n+1))/(17^(n+1)) and compared with the given answer choices.

A series with a limit of a_n+1/a_n equal to three as n approaches infinity is analyzed for convergence.

The series a_n * 5^n is shown to converge by altering the Ratio Test to give a limit less than one.

The summation of the series where a_n equals one for all positive integers is identified as the nth partial sum being equal to n.

The video concludes with a promise to continue the series in future parts, available in a playlist.

Transcripts

Browse More Related Video

Calculus Chapter 5 Lecture 52 Convergence Tests 2

Infinite Series Multiple Choice Practice for Calc BC (Part 5)

Tests for Convergence

Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test

Infinite Series Multiple Choice Practice for Calc BC (Part 2)

Calculus BC – 10.3 The nth Term Test for Divergence

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusSeries ConvergenceIntegral Testnth Term TestMathematicsExam PrepEducationalRatio TestSummationRiemann SumsVideo Tutorial