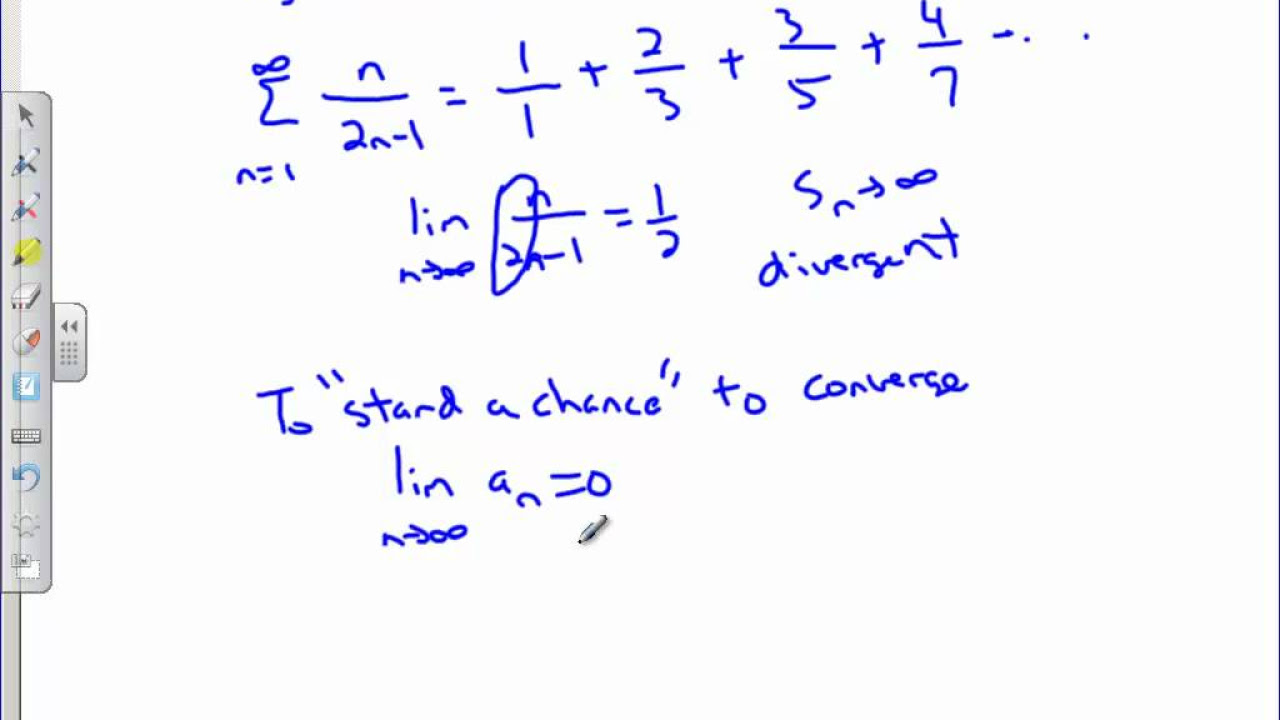Calculus BC – 10.3 The nth Term Test for Divergence
TLDRIn this calculus lesson by Mr. Bean, students learn about the nth term test for divergence, a straightforward method to determine if a series diverges by examining the behavior of its terms as 'n' approaches infinity. The key takeaway is that if the limit of the series' last term is not zero, the series diverges; however, if it equals zero, the test is inconclusive. The lesson includes practical examples and emphasizes that while the nth term test can confirm divergence, it cannot confirm convergence, requiring additional strategies for a definitive conclusion.
Takeaways
- 📚 The lesson is about the nth term test for divergence in calculus, presented by Mr. Bean.
- 🔍 The nth term test involves examining the behavior of the nth term of a series as n approaches infinity.
- 🌟 If the limit of the last term as n approaches infinity equals zero, the series may converge or diverge; this cannot be determined solely by this test.
- ❌ A common misconception is that if the limit of the last term is zero, the series converges, but this is not necessarily true.
- 🛑 The nth term test can definitively conclude divergence if the limit of the last term as n approaches infinity does not equal zero.
- 📉 The test is used to identify if a series diverges, not to confirm convergence, which requires additional strategies.
- 📝 Practice problems are used to illustrate the application of the nth term test, emphasizing the importance of recognizing patterns like geometric series.
- 📈 In a geometric series, if the absolute value of the common ratio (r) is less than one, the series converges without needing the nth term test.
- 🤓 For series that are not geometric, the nth term test can provide no conclusion, and further analysis is required to determine convergence or divergence.
- 📚 The lesson includes a step-by-step approach to applying the nth term test, including handling typos and errors in calculations.
- 🎓 The importance of understanding horizontal asymptotes and recognizing series types, such as geometric, is highlighted for effective use of the nth term test.
Q & A
What is the main topic of the lesson presented by Mr. Bean?
-The main topic of the lesson is the nth term test for divergence in calculus.
Why does Mr. Bean describe the nth term test as 'easy'?
-Mr. Bean describes the nth term test as 'easy' because it is a straightforward concept that can quickly determine if a series diverges, compared to other more complex calculus lessons.
What does the nth term test for divergence involve?
-The nth term test for divergence involves examining the behavior of the nth term of a series as n approaches infinity to determine if the series converges or diverges.
According to the nth term test, what condition indicates that a series might converge?
-According to the nth term test, if the limit of the nth term as n approaches infinity equals zero, the series might converge, but this does not guarantee convergence.
What conclusion can be drawn if the limit of the nth term does not equal zero as n approaches infinity?
-If the limit of the nth term does not equal zero as n approaches infinity, the series diverges.
Why can't we conclude that a series converges just because the limit of the nth term equals zero?
-We can't conclude that a series converges just because the limit of the nth term equals zero because it only indicates the series might converge; it could also diverge.
What is a common mistake students make regarding the nth term test?
-A common mistake students make is assuming that if the limit of the nth term equals zero, the series must converge, which is not necessarily true.
How does Mr. Bean simplify the notation when applying the nth term test?
-Mr. Bean simplifies the notation by using 'a sub n' to represent the nth term of the series instead of rewriting the entire expression.
In the lesson, what is an example of a series that the nth term test cannot conclusively determine as converging or diverging?
-An example given is a geometric series with a common ratio of one half, where the nth term test shows the limit approaches zero, indicating no conclusive result about convergence or divergence.
What is the significance of recognizing a series as geometric when applying the nth term test?
-Recognizing a series as geometric is significant because it allows for immediate determination of convergence without needing to apply the nth term test, as geometric series with an absolute ratio less than one are known to converge.
How does Mr. Bean demonstrate the application of the nth term test using a series with a complex expression?
-Mr. Bean demonstrates by simplifying the expression to focus on the dominant terms as n approaches infinity, which allows for determining the limit of the nth term and applying the nth term test to conclude if the series diverges.
What is the conclusion of the nth term test for a series where the limit of the nth term approaches a non-zero value?
-If the limit of the nth term approaches a non-zero value as n approaches infinity, the conclusion of the nth term test is that the series diverges.
How does Mr. Bean handle a situation where the nth term test does not provide a clear conclusion about the series?
-Mr. Bean explains that in such cases, no conclusion can be made using the nth term test alone, and other strategies or tests may be needed to determine the behavior of the series.
Outlines
📚 Introduction to the nth Term Test for Divergence
In this lesson, Mr. Bean introduces the nth term test for divergence, a method used to determine if a series diverges. He emphasizes that the test is straightforward and assures students that it will be an easy topic. The nth term test involves examining the behavior of the nth term of a series as n approaches infinity. If the limit of the nth term equals zero, the series may converge, but this is not definitive. The key takeaway is that if the limit of the nth term does not equal zero, the series definitely diverges. Mr. Bean also clarifies that the converse is not true: a limit of zero does not guarantee convergence. He then proceeds to demonstrate the test with practice problems, illustrating how to apply the nth term test to determine divergence.
🔍 Applying the nth Term Test to Various Series
Mr. Bean continues the lesson by applying the nth term test to different series. He explains that if the limit of the nth term as n approaches infinity equals zero, no conclusion can be made about convergence or divergence. However, if the limit does not equal zero, the series diverges. He demonstrates this with several examples, correcting a typo in one of the problems and emphasizing the importance of recognizing the largest terms in the series when determining the limit. He also discusses geometric series, noting that if the absolute value of the common ratio is less than one, the series converges. Mr. Bean uses the nth term test to show that certain series do not converge, and he highlights the importance of recognizing geometric series to avoid unnecessary calculations. The lesson concludes with a brief mention of future lessons that will delve deeper into determining convergence or divergence.
Mindmap
Keywords
💡nth term test for divergence
💡convergence
💡divergence
💡series
💡limit
💡horizontal asymptotes
💡geometric series
💡l'Hôpital's rule
💡practice problems
💡conclusion statement
Highlights
Introduction to the nth term test for divergence in calculus.
The simplicity of the nth term test compared to other calculus lessons.
Explanation of the nth term test: if the limit of the last term as n approaches infinity equals zero, the series might converge or diverge.
Clarification that a limit of zero for the last term does not guarantee convergence.
The nth term test's ability to definitively conclude divergence if the limit of the last term does not equal zero.
Demonstration of using the nth term test with practice problems.
Example of a series where the nth term test shows divergence due to a non-zero limit.
Mistake correction in the transcript and apology for the typo.
The importance of recognizing geometric series for quick convergence determination.
Application of the nth term test to a geometric series where the conclusion is indeterminate.
Explanation of how to handle series that do not have a clear common ratio for the nth term test.
Demonstration of a series where the nth term test cannot provide a conclusion due to the limit approaching zero.
Analysis of a series with terms that cancel out, leaving a non-zero limit, indicating divergence.
Use of l'Hôpital's rule as an alternative method for determining the limit in certain series.
Final example of a series where the nth term test concludes divergence due to an exponential numerator outgrowing a linear denominator.
Summary of the lesson's ease and the expectation of a short packet for practice.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: