Lecture 3 | The Theoretical Minimum
TLDRThe video script delves into the mathematical foundations of quantum mechanics, with a focus on linear algebra and the concept of operators within vector spaces. It explains the notation and manipulation of vectors, the space of states, and the importance of understanding good notation for abstract mathematics. The lecture introduces the idea of a linear operator as a machine that transforms input vectors into output vectors, obeying the rules of linearity. It also discusses the properties of Hermitian matrices, their significance in representing observable quantities in quantum mechanics, and their relationship with eigenvalues and eigenvectors. The script further explores the postulates of quantum mechanics, detailing how the measurement process leads to definite outcomes and how probabilities are calculated in the quantum realm. The Pauli matrices, representing the components of spin in different directions, are also examined. The content is rich in mathematical formalism and provides a comprehensive understanding of the principles underlying quantum mechanics.
Takeaways
- 📚 Good notation is crucial in mathematics and physics for easily manipulating symbols and performing abstract mathematics.
- 📐 In a vector space, the dimensionality is the maximum number of orthogonal vectors that can be found, and it defines the basis of vectors.
- 🔍 Any vector in a space can be written as a sum over its basis vectors, multiplied by complex coefficients, which are the components of the vector.
- 🧮 The inner product of a vector with a basis vector allows us to find the coefficients (or components) of the vector in terms of the basis.
- 🤔 The concept of linear operators is central to quantum mechanics, where states are vectors and observables are related to linear operators.
- 📊 A linear operator acting on a vector space follows specific rules, such as acting on a constant times a vector to give back the constant times the output vector.
- 🧘 The action of a linear operator can be represented by a matrix, which is a collection of matrix elements, and can be manipulated arithmetically.
- 🌐 The matrix representation of a linear operator depends on the chosen basis, highlighting the trade-off between geometric understanding and computational ease.
- ✨ Hermitian matrices, which are equal to their own Hermitian conjugate, have real diagonal elements and are of significant importance in quantum mechanics as they represent observable quantities.
- ⚖️ Eigenvalues of Hermitian matrices are real, and if two eigenvalues are different, their corresponding eigenvectors are orthogonal.
- 🎯 The principles of quantum mechanics can be stated mathematically, relating the physical meanings of probability, state vectors, and the statistical nature of measurement outcomes to their mathematical representations.
Q & A
What is the significance of good notation in mathematics and physics?
-Good notation is crucial as it allows for easier manipulation of symbols in a pre-arranged manner, which simplifies the process of doing abstract mathematics and dealing with mathematical abstractions in physics.
What is a linear vector space?
-A linear vector space is a collection of abstract vectors where you can multiply states by numbers to get new states and perform addition. It has a property of dimensionality, which is the maximum number of orthogonal vectors that can be found in the space.
What are the two types of vectors in the context of quantum mechanics?
-In quantum mechanics, there are bra vectors and ket vectors. They are related by complex conjugation, and together they form the basis for describing quantum states.
What is the concept of a basis in a vector space?
-A basis in a vector space is a mutually orthogonal collection of normalized vectors (orthonormal basis) that spans the space. It defines the maximum number of independent directions in the space, and any vector in the space can be written as a sum over these basis vectors.
How is the inner product used to find the coefficients of a vector in terms of a basis?
-The inner product is used by taking the inner product of both sides of the equation with a basis vector. This results in the coefficients being equal to the inner product of the basis vector with the target vector.
What is a linear operator?
-A linear operator is a process that acts on an input vector to produce an output vector. It follows two main rules: it maps a scalar multiple of a vector to the same scalar multiple of the output, and it maps the sum of two vectors to the sum of their images.
How are linear operators represented in terms of matrix elements?
-Linear operators can be represented by their matrix elements, which are the inner products of the operator acting on basis vectors with other basis vectors. These matrix elements allow us to compute the components of the output vector in terms of the input vector's components.
What is the role of Hermitian matrices in quantum mechanics?
-Hermitian matrices, which are equal to their own Hermitian conjugate, play a significant role in quantum mechanics as they represent observable quantities. Their eigenvalues correspond to the possible results of measurements, and their eigenvectors correspond to the states with definite values for the observable.
What is the relationship between the matrix elements of a linear operator and its Hermitian conjugate?
-The matrix element of the Hermitian conjugate of a linear operator is the complex conjugate of the transpose of the original matrix element, which means you interchange the row and column indices of the original matrix and take the complex conjugate.
What are the properties of a Hermitian matrix?
-A Hermitian matrix has real diagonal elements and off-diagonal elements that are complex conjugates of each other when reflected across the diagonal. This type of matrix is used to represent observable quantities in quantum mechanics.
How do you determine if a matrix is a Hermitian matrix?
-To determine if a matrix is a Hermitian matrix, check if the matrix is equal to its own Hermitian conjugate, which means the matrix has real diagonal elements and off-diagonal elements that are the complex conjugates of their transposed positions.
Outlines
📚 Introduction to Mathematical Notation in Linear Algebra
The video begins with an introduction to mathematical interlude focusing on linear algebra, specifically vector spaces and operators. The importance of good notation in abstract mathematics and physics is emphasized, highlighting its role in manipulating symbols efficiently. The concept of a space of states as a linear vector space is introduced, where states can be multiplied by complex numbers to create new states. The video also differentiates between bra and ket vectors and discusses the dimensionality of a vector space, the significance of finding a basis of orthonormal vectors, and how any vector can be expressed as a sum over these basis vectors.
🧮 Inner Product and Expansion of Vectors in Terms of Basis
The paragraph explains how to calculate coefficients (Alpha sub Is) in the expansion of any vector using the inner product with basis vectors. It is shown that the coefficients can be found by taking the inner product of the basis vector with the target vector. The concept is illustrated through a formula that allows any vector to be rewritten in terms of its coefficients or inner products with the basis vectors. The same principle is shown to apply for bra vectors, and the paragraph emphasizes the utility and power of these simple mathematical abstractions.
🔍 Linear Operators and Their Action on Vectors
The video introduces linear operators in quantum mechanics, which are represented as machines that take an input vector and produce an output vector. Linear operators are characterized by two main properties: they distribute over vector addition and they are compatible with scalar multiplication. The action of a linear operator on a vector is concretely illustrated by projecting the output vector onto a basis vector and finding its components. The concept of matrix elements is introduced as a way to characterize linear operators.
📏 Matrix Representation of Linear Operators
The paragraph delves into the matrix representation of linear operators, explaining that a matrix is a concrete representation of an operator with specific components. It is shown that the matrix elements can be found by taking the inner product of the operator's action on basis vectors with another basis vector. The matrix is defined as an N by N square matrix if the space's dimensionality is N. The video also explains that the matrix representation depends on the choice of basis vectors, and different choices can lead to different matrix elements.
🤔 Action of Linear Operators on Bra Vectors
The discussion extends to the action of linear operators on bra vectors, emphasizing the standard notation where the operator acts to the right of the bra vector. The video presents a method to define the action of an operator on a bra vector, ensuring that the order of brackets does not affect the outcome. The concept of Hermitian conjugation (dagger) is introduced, which is related to complex conjugation and is used to define the action on bra vectors.
🌟 Hermitian Matrices and Observables in Quantum Mechanics
The video defines Hermitian matrices and operators, which are equal to their own Hermitian conjugate. It is shown that the diagonal elements of a Hermitian matrix are always real, and the off-diagonal elements are complex conjugates of each other. Hermitian matrices are significant in quantum mechanics as they represent observable quantities. The concept of eigenvectors and eigenvalues is introduced, with a focus on their properties when associated with Hermitian operators.
🎯 Eigenvectors and Eigenvalues of Hermitian Matrices
The paragraph explores the properties of eigenvectors and eigenvalues of Hermitian matrices, proving that if two eigenvectors correspond to different eigenvalues, they must be orthogonal. This orthogonality is linked to the physical concept that measurements can distinguish between different states unambiguously. The video also discusses the probabilistic nature of quantum mechanics, where the probability of measuring a particular eigenvalue is given by the square of the inner product of the state vector with the corresponding eigenvector.
🧲 Principles of Quantum Mechanics and Measurement
The video outlines the basic principles of quantum mechanics, stating that measurable quantities yield real numbers and that observables are represented by Hermitian operators. It is explained that the eigenvalues of an observable are the possible outcomes of a measurement, and the eigenvectors correspond to states where the observable has a definite value. The principles also include the idea that measuring a quantity collapses the system into an eigenstate corresponding to the measured eigenvalue.
🌀 Normalization and Phase Invariance in Quantum States
The paragraph discusses the concept of normalization in quantum states, where the sum of the squares of the probabilities (associated with each possible outcome of a measurement) must equal one. It also touches on the idea of phase invariance, where multiplying the state vector by a phase factor does not change the probabilities of measurement outcomes. This implies that there are fewer independent parameters in the specification of a state than the number of complex numbers defining a vector in the abstract space.
🎚️ Sigma Matrices and Their Eigenvectors
The video concludes with an exploration of the sigma matrices (Pauli matrices), which represent the components of spin in different directions. It is shown that these matrices have specific eigenvectors and eigenvalues, and the matrix elements can be computed in a chosen basis. The discussion also involves the transformation between different bases, such as from the 'up' and 'down' basis to the 'left' and 'right' basis.
🏁 Conclusion and Future Directions
The video wraps up with a summary of the concepts covered and hints at future topics, such as calculating the probability of measuring the z-component of spin in an arbitrary direction using the principles discussed. It invites further exploration of quantum mechanics and encourages the audience to apply the mathematical formalism to specific problems.
Mindmap
Keywords
💡Linear Algebra
💡Vector Space
💡Basis Vectors
💡Orthonormal Basis
💡Linear Operator
💡Hermitian Operator
💡
💡Eigenvalues and Eigenvectors
💡Quantum Mechanics
💡Pauli Matrices
💡Inner Product
💡Complex Conjugation
Highlights
Introduction to mathematical interlude focusing on linear algebra, vector spaces, and operators.
Emphasis on the importance of good notation in abstract mathematics and physics.
Explanation of the space of states as a linear vector space where states can be multiplied by complex numbers.
Discussion on the two types of vectors: bra and ket, and their relation through complex conjugation.
Clarification of vector space dimensionality and the concept of an orthonormal basis.
Method to calculate complex coefficients (Alpha sub I) using inner products with basis vectors.
Introduction to linear operators in the context of quantum mechanics as observables.
Description of a linear operator as a process or 'machine' that transforms input vectors to output vectors.
Rules defining a linear operator, including actions on constants times vectors and sums of vectors.
Concrete representation of linear operators through matrix elements and their computation.
Explanation of how to find the components of a vector when acted upon by a linear operator.
Insight into the relationship between linear operators and matrices, including matrix multiplication with column vectors.
Discussion on the dependence of matrix elements on the choice of basis vectors.
Introduction to the concept of Hermitian operators and their significance in quantum mechanics.
Procedure to determine the Hermitian conjugate of an operator, involving complex conjugation and transposition.
Properties of Hermitian matrices, including real diagonal elements and a specific type of off-diagonal symmetry.
The eigenvectors and eigenvalues of Hermitian matrices and their role in representing observable quantities in quantum mechanics.
Postulates of quantum mechanics relating to the measurement process, probability amplitudes, and the normalization of state vectors.
Explanation of how the measurement of an observable prepares the system in an eigenstate corresponding to the measured value.
Application of quantum mechanics principles to the spin system, exploring the properties of sigma matrices (Sigma X, Sigma Y, and Sigma Z).
Transcripts
Browse More Related Video

Lecture 3 | Quantum Entanglements, Part 1 (Stanford)

Ch 2: What are kets and wavefunctions? | Maths of Quantum Mechanics

Lecture 2 | Quantum Entanglements, Part 1 (Stanford)

Lecture 4 | The Theoretical Minimum
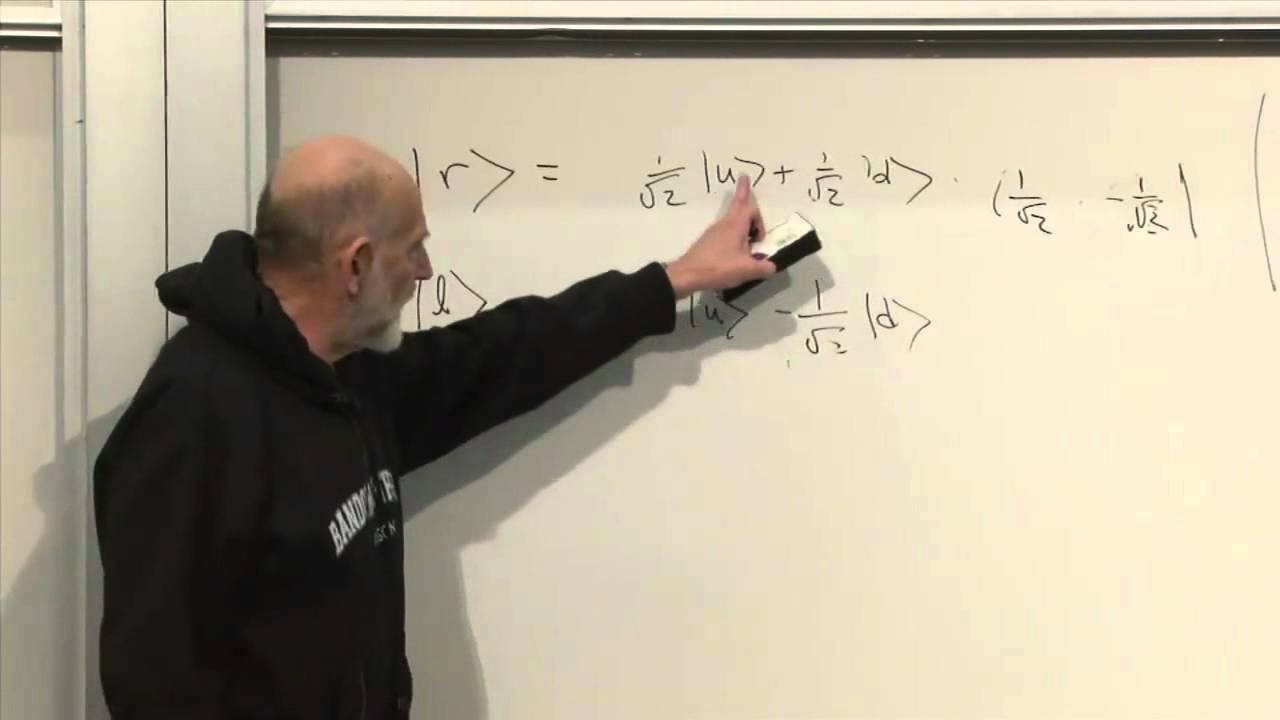
Lecture 2 | The Theoretical Minimum

Ch 3: Why do we need a Hilbert Space? | Maths of Quantum Mechanics
5.0 / 5 (0 votes)
Thanks for rating: