Implicit Differentiation With Partial Derivatives Using The Implicit Function Theorem | Calculus 3

The Organic Chemistry Tutor
31 Oct 201911:11
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a comprehensive tutorial on finding partial derivatives using the Implicit Function Theorem and an alternative method, implicit differentiation. The first example involves an equation with variables x, y, and z, where the partial derivatives of z with respect to x and y are sought. By rearranging the equation and applying the Implicit Function Theorem, the partial derivatives are found to be (2x + 3y^2) / (3z^2) and (4y^3 + 6xy) / (3z^2), respectively. An alternative approach using implicit differentiation yields the same results, demonstrating its equivalence. A second example further illustrates the process with a different equation, reinforcing the application of these mathematical techniques. The script is an engaging and informative resource for those interested in calculus and the mechanics of finding partial derivatives.

Takeaways
  • 📘 Implicit Function Theorem is used to find partial derivatives of functions that are not explicitly defined in terms of one variable.
  • 🔍 Start by setting the equation to zero and representing it as a function f(x, y) = 0.
  • ➗ To find the partial derivative with respect to x, treat y and z as constants and differentiate each term.
  • ✅ For f_x, the partial derivative of z with respect to x, use the formula z_x = -f_x / f_z.
  • 🔄 Repeat the process for the partial derivative with respect to y, treating x and z as constants to find f_y and then z_y.
  • 📐 When differentiating terms with variables, apply the power rule and chain rule as necessary.
  • 🚫 Constants and terms without the variable of interest will have a derivative of zero.
  • 🔢 The partial derivatives are found by isolating the variable of interest and solving for it.
  • ➖ Negative signs in the derivatives can often be factored out to simplify the final expression.
  • 📉 Implicit differentiation is an alternative method to find partial derivatives without explicitly using the Implicit Function Theorem.
  • 📚 Practice is key to mastering the process of finding partial derivatives, as demonstrated by working through additional examples.
  • 📌 Remember to check for any mistakes in the differentiation process, such as the sign error in the script for the term involving y squared.
Q & A

  • What is the main concept used to find the partial derivatives in the video?

    -The main concept used to find the partial derivatives is the Implicit Function Theorem, which allows us to differentiate an equation with respect to one variable while treating the other variables as constants.

  • How do you move the constant term to the other side of the equation?

    -In the video, the constant term (like 8) is moved to the other side of the equation by subtracting it from both sides, resulting in an equation equal to zero.

  • What is the first step in finding the partial derivative of z with respect to x?

    -The first step is to differentiate each term of the equation with respect to x, treating y and z as constants, and then simplify the resulting expression to find the partial derivative f_x.

  • What is the mistake made in the video when finding the partial derivative with respect to y?

    -The mistake made in the video is the incorrect sign for the term involving '3xy^2'; it should be positive instead of negative when finding the partial derivative f_y.

  • How do you find the partial derivative of z with respect to x using the Implicit Function Theorem?

    -You find the partial derivative of z with respect to x (denoted as z_x) by using the formula z_x = -f_x / f_z, where f_x is the partial derivative of the function with respect to x and f_z is the partial derivative with respect to z.

  • What is the process to find the partial derivative of z with respect to y?

    -To find the partial derivative of z with respect to y (denoted as z_y), you differentiate the equation with respect to y, treating x and z as constants, and then use the formula z_y = -f_y / f_z, where f_y is the partial derivative with respect to y.

  • What is another method to find the partial derivatives of z with respect to x and y?

    -Another method is to use implicit differentiation directly on the given equation, treating the variables x and y as the primary variables of differentiation and isolating the partial derivatives of z as done in the video.

  • What is the role of treating other variables as constants during differentiation?

    -When differentiating with respect to one variable, treating other variables as constants allows us to focus solely on the derivative of the term involving the variable of interest, which simplifies the differentiation process.

  • How do you correct the sign error made in the video for the term involving '3xy^2'?

    -The term '3xy^2' should have a positive sign when taking the derivative with respect to y, as the derivative of y^2 with respect to y is 2y, and when multiplied by the constant 3x, it results in a positive term, 6xy.

  • What is the final expression for the partial derivative of z with respect to x after correcting the sign error?

    -After correcting the sign error, the final expression for the partial derivative of z with respect to x (z_x) is 2x + 3y^2 / 3z^2.

  • What is the final expression for the partial derivative of z with respect to y after the differentiation process?

    -The final expression for the partial derivative of z with respect to y (z_y) is 4y^3 + 6xy / 3z^2.

  • What is the significance of the Implicit Function Theorem in solving for partial derivatives in this context?

    -The Implicit Function Theorem allows us to solve for partial derivatives even when the function is not explicitly defined in terms of the variable of interest, which is often the case in complex equations involving multiple variables.

Outlines
00:00
🧮 Implicit Function Theorem and Partial Derivatives

This paragraph introduces the process of finding partial derivatives using the implicit function theorem. The equation involves variables x, y, and z, and the goal is to find the partial derivatives of z with respect to x and y. The explanation begins by rearranging the equation to set it equal to zero, then differentiating with respect to x and y while treating other variables as constants. The partial derivatives are calculated for each variable, and the results are simplified to express z with respect to x and y. An alternative method, implicit differentiation, is also discussed to derive the same results, providing a comprehensive understanding of the concept.

05:03
🔍 Isolating and Solving for Partial Derivatives

The second paragraph focuses on isolating and solving for the partial derivatives of z with respect to x and y using implicit differentiation. The process involves differentiating each term of the equation with respect to x and y, treating other variables as constants where necessary. The partial derivatives are then solved for by rearranging terms and factoring out constants to simplify the expressions. The method is demonstrated by moving terms to one side and factoring to cancel out negative signs, resulting in the final expressions for the partial derivatives of z with respect to both x and y. The paragraph emphasizes the step-by-step approach to solving these types of calculus problems.

10:03
📚 Applying the Implicit Function Theorem to a New Example

The final paragraph presents a new example to practice applying the implicit function theorem. The equation is rearranged to isolate a function of x and y, and partial derivatives with respect to x and y are sought. The process involves differentiating each term with respect to the variable of interest, treating other variables as constants. The partial derivatives are then calculated, and the results are simplified. The paragraph concludes with the final expressions for the partial derivatives of z with respect to x and y, reinforcing the method's application in calculus problems.

Mindmap
Keywords
💡Implicit Function Theorem
The Implicit Function Theorem is a fundamental theorem in calculus that allows us to find the derivatives of implicitly defined functions. In the video, it is used to find the partial derivatives of z with respect to x and y. It is a key concept because it provides a method to solve for the partial derivatives when the function is not explicitly defined in terms of z.
💡Partial Derivative
A partial derivative is a derivative that measures how a function changes with respect to a single variable while keeping all other variables constant. In the video, the partial derivatives of z with respect to x and y are calculated using both the Implicit Function Theorem and implicit differentiation, which shows two different methods to achieve the same result.
💡Differentiation
Differentiation is a process used in calculus to find the rate at which a function is changing at a certain point. In the context of the video, differentiation is used to find the partial derivatives of the given equations with respect to x and y. It is a fundamental operation in the process of finding the rate of change in the variables.
💡Constants
In the context of differentiation, constants are terms that do not change with respect to the variable being differentiated. In the video, when differentiating with respect to x, y and z are treated as constants, and vice versa. This simplifies the differentiation process and allows for the isolation of terms that do contain the variable of interest.
💡Equation Rearrangement
Equation rearrangement is a mathematical technique used to isolate terms and set the equation to zero for easier manipulation. In the video, the script describes moving constants to one side of the equation to facilitate the application of the Implicit Function Theorem. This step is crucial for setting up the equation in a form that allows for differentiation.
💡Implicit Differentiation
Implicit differentiation is a method used to differentiate equations where the variable of interest is not explicitly isolated. It involves differentiating every term of the equation with respect to the variable, treating other variables as constants when necessary. The video demonstrates this method as an alternative way to find the partial derivatives of z with respect to x and y.
💡Treating Variables as Constants
When differentiating with respect to a specific variable, other variables are often treated as constants. This is a simplification that allows for the differentiation process to proceed without having to account for the rate of change of these other variables. In the video, when finding the partial derivative of z with respect to x, y and z are treated as constants.
💡Zero on the Right Side
Setting the equation to equal zero is a common technique in calculus, especially when applying the Implicit Function Theorem. In the video, the script describes rearranging terms so that all terms involving the variable of interest are on one side of the equation and the constant is on the other, facilitating the differentiation process.
💡Function Representation
In the context of the video, function representation refers to expressing the given equation in a form where one variable is implicitly defined by the equation. This is necessary for applying the Implicit Function Theorem. The video demonstrates how to represent the equation in terms of f(x, y) and then use this representation to find the partial derivatives.
💡Simplifying Expressions
Simplifying expressions is a crucial step in calculus that helps to reduce complex equations to a more manageable form. In the video, after finding the partial derivatives using the Implicit Function Theorem and implicit differentiation, the expressions are simplified to their most straightforward form to present the final answers.
💡Negative Signs
The handling of negative signs is important in calculus, especially when dealing with derivatives and fractions. In the video, the script discusses how to manage negative signs when calculating the partial derivatives, including canceling them out to simplify the final expressions.
Highlights

Introduction to finding partial derivatives of a function with respect to multiple variables using the implicit function theorem.

Rearrangement of the given equation to set it equal to zero for easier differentiation.

Differentiation of x squared, treating y and z as constants, resulting in 2x.

Derivation of the partial derivative of z with respect to x as 2x - 3y^2.

Derivation of the partial derivative of z with respect to y as 4y^3 + 6xy.

Correction of a mistake in the sign for the term involving y and x.

Calculation of the partial derivative of z with respect to x using the formula z_x = -f_x / f_z.

Simplification of the expression for z_x to 2x + 3y^2 / 3z^2.

Calculation of the partial derivative of z with respect to y using the formula z_y = -f_y / f_z.

Simplification of the expression for z_y to 4y^3 + 6xy / 3z^2.

Introduction of an alternative method for finding partial derivatives using implicit differentiation.

Differentiation of the equation with respect to x to find the partial derivative of z with respect to x.

Isolation and simplification of terms to find the expression for the partial derivative of z with respect to x.

Differentiation of the equation with respect to y to find the partial derivative of z with respect to y.

Isolation and simplification of terms to find the expression for the partial derivative of z with respect to y.

Presentation of a second example to practice finding partial derivatives using the implicit function theorem.

Differentiation of the new equation with respect to x and y to find the respective partial derivatives.

Calculation of the partial derivative of z with respect to x (z_x) and z with respect to y (z_y) for the second example.

Final expression for z_x and z_y in the second example, showcasing the application of the implicit function theorem.

Transcripts

Browse More Related Video

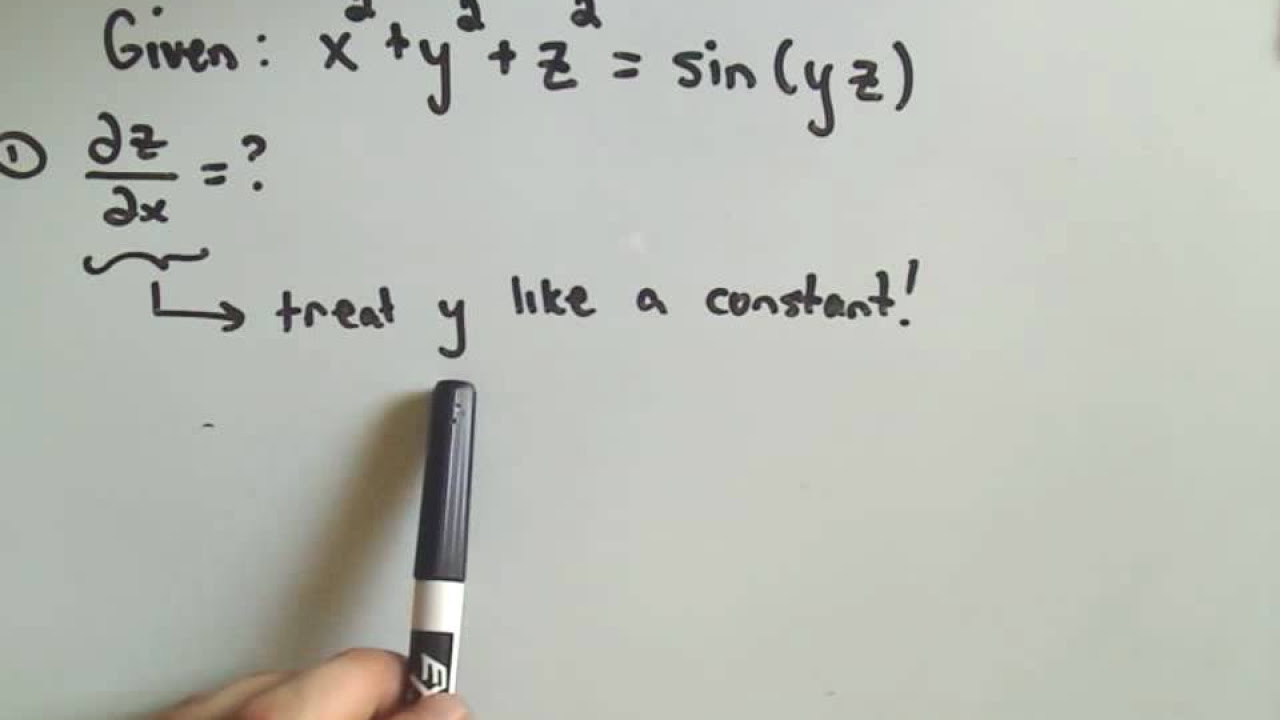
MultiVariable Calculus - Implicit Differentiation

Implicit Differentiation Method

Calculating Partial Derivatives with PyTorch AutoDiff — Topic 69 of Machine Learning Foundations

Partial Derivatives

Second derivatives (implicit equations): find expression | AP Calculus AB | Khan Academy

Symmetry of second partial derivatives

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Implicit FunctionPartial DerivativesMathematical AnalysisEquation SolvingTheorem ApplicationDifferentiation TechniquesCalculus TutorialHigher MathematicsEducational ContentMathematical ConceptsLearning Resource