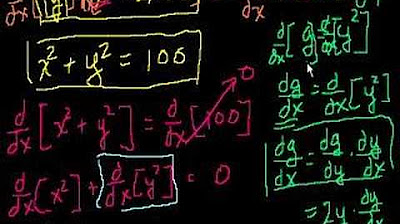Second derivatives (implicit equations): find expression | AP Calculus AB | Khan Academy

Khan Academy
7 May 201804:47
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a step-by-step guide on finding the second derivative of y with respect to x for the given equation y^2 - x^2 = 4 using implicit differentiation. The process involves taking the first derivative to isolate dy/dx, and then using the product rule and chain rule to compute the second derivative, resulting in an expression of -x^2/y^3. The explanation is clear, emphasizing the application of fundamental calculus concepts.

Takeaways
  • 📚 The given equation is y^2 - x^2 = 4, and the goal is to find the second derivative of y with respect to x.
  • 🔍 Implicit differentiation is used as it avoids solving for y, which could involve square roots and complicate the process.
  • 📈 The first step is to find the first derivative of y with respect to x, using the chain rule and basic differentiation rules.
  • 🌟 The first derivative is found to be (dy/dx) = x/y by applying the chain rule and simplifying the equation.
  • 🔄 To find the second derivative, we take the derivative of both sides of the first derivative equation with respect to x.
  • 📝 The quotient rule and product rule are applied to the second derivative calculation, which involves rewriting the first derivative as a product for easier manipulation.
  • 🎓 The derivative of y^(-1) is calculated using the power rule, which is crucial for finding the second derivative.
  • 🔢 The second derivative (d^2y/dx^2) is simplified to be -x^2/(y^3), which is the final expression in terms of x and y.
  • 💡 The process demonstrates the importance of understanding and applying the chain rule, product rule, and power rule in differentiation.
  • 📊 The example serves as a clear illustration of how to handle complex differentiation problems involving quadratic expressions.
  • 🌐 The solution maintains a focus on the mathematical process, without the need to solve for y explicitly, showcasing an efficient approach to problem-solving.
Q & A

  • What is the given equation in the problem?

    -The given equation is y^2 - x^2 = 4.

  • What is the goal of the problem?

    -The goal is to find the second derivative of y with respect to x and express it in terms of x and y.

  • Why might solving for y not be the best approach in this problem?

    -Solving for y might not be the best approach because the presence of y^2 could involve taking a square root, which may complicate the differentiation process.

  • What alternative method is suggested for solving the problem?

    -The alternative method suggested is implicit differentiation, which is an application of the chain rule.

  • What is the first step in using implicit differentiation?

    -The first step is to find the first derivative of y with respect to x by taking the derivative of both sides of the given equation with respect to x.

  • What is the expression for the first derivative of y with respect to x?

    -The first derivative of y with respect to x is (dy/dx) = x / y.

  • How is the second derivative of y with respect to x found?

    -The second derivative is found by taking the derivative of the expression for the first derivative (dy/dx) = x / y with respect to x.

  • What mathematical rule is used to find the derivative of the expression x / y?

    -The quotient rule is used to find the derivative of the expression x / y.

  • What is the final expression for the second derivative of y with respect to x?

    -The final expression for the second derivative of y with respect to x is (d^2y/dx^2) = -x^2 / y^3.

  • How does the problem demonstrate the application of the chain rule?

    -The problem demonstrates the application of the chain rule in finding the first and second derivatives of y with respect to x, especially when dealing with the y^2 term and the x / y expression.

  • What is the significance of the power rule in this problem?

    -The power rule is significant in this problem when finding the derivative of y to the negative one power, which is part of the process to calculate the second derivative.

Outlines
00:00
📚 Introduction to Implicit Differentiation

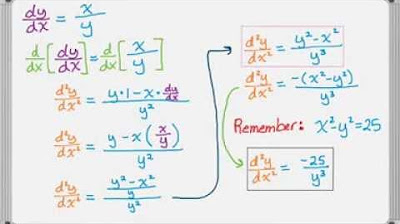
This paragraph introduces the concept of implicit differentiation as a method to find the derivative of a function that is not explicitly expressed in terms of one variable. The instructor presents an equation, y squared minus x squared equals four, and sets a goal to find the second derivative of y with respect to x. The paragraph explains the process of taking the first derivative using the chain rule and then proceeds to find the second derivative by applying the product rule and power rule. The explanation is detailed, walking through each step of the differentiation process, including handling the constant term and the quotient rule. The paragraph concludes with the final expression for the second derivative, which is minus x squared over y cubed.

Mindmap
Keywords
💡Implicit Differentiation
Implicit differentiation is a method used to find the derivatives of functions when the equation is not explicitly solved for the variable of interest. In the video, it is used to find the first derivative of y with respect to x without solving for y directly. This technique relies on the chain rule and involves differentiating both sides of the given equation with respect to x to derive the relationship between dy/dx and the variables x and y.
💡Chain Rule
The chain rule is a fundamental concept in calculus that is used to find the derivative of a composite function. It states that the derivative of a function that is the result of another function(s) is the product of the derivative of the outer function evaluated at the inner function and the derivative of the inner function. In the video, the chain rule is applied when differentiating y^2 with respect to x, recognizing y^2 as a composite function of y and x.
💡First Derivative
The first derivative of a function represents the rate of change or the slope of the function at any given point. In the context of the video, the first derivative of y with respect to x is found by differentiating both sides of the equation y^2 - x^2 = 4. The result is an expression that gives the rate of change of y with respect to x, which is crucial for further analysis, such as finding the second derivative.
💡Second Derivative
The second derivative of a function is the derivative of the first derivative. It provides information about the concavity of a function and can indicate points of inflection or changes in the curvature of the function's graph. In the video, the second derivative of y with respect to x is calculated by differentiating the expression obtained for the first derivative, which helps in understanding the behavior of the original function y^2 - x^2 = 4.
💡Quotient Rule
The quotient rule is a mathematical principle used in calculus to find the derivative of a quotient of two functions. It states that the derivative of a function f(x) divided by a function g(x) is equal to the derivative of f(x) multiplied by g(x) minus f(x) multiplied by the derivative of g(x), all divided by the square of g(x). In the video, the quotient rule is mentioned as a potential tool for finding the second derivative but is not directly applied; instead, the product rule is used after rewriting the expression for the first derivative.
💡Product Rule
The product rule is a fundamental calculus rule used to find the derivative of a product of two functions. It states that the derivative of two functions multiplied together is the first function times the derivative of the second function plus the second function times the derivative of the first function. In the video, the product rule is applied to find the second derivative of y with respect to x by differentiating the expression for the first derivative, which was obtained through implicit differentiation.
💡Power Rule
The power rule is a basic differentiation rule in calculus that allows the derivative of a function of the form f(x) = x^n to be found as f'(x) = n * x^(n-1), where n is a constant. In the video, the power rule is used to find the derivative of y^(-1), which is a key step in calculating the second derivative of the given equation.
💡Derivative of a Constant
The derivative of a constant is always zero because a constant does not change with respect to the variable. In the context of the video, when differentiating the constant term in the equation y^2 - x^2 = 4 with respect to x, the result is zero, as expected.
💡Simplifying Expressions
Simplifying expressions involves using arithmetic and algebraic rules to reduce mathematical expressions to their simplest form. In the video, the instructor simplifies the expression for the second derivative by combining like terms and applying the rules of exponents, resulting in a more manageable form of the derivative.
💡Rate of Change
The rate of change, or the derivative, describes how a function changes as its input variable changes. It provides information about the slope of the function's graph at any given point. In the video, the first and second derivatives of y with respect to x are calculated to understand the rate of change and the concavity of the function described by the equation y^2 - x^2 = 4.
💡Differentiation
Differentiation is the process of finding the derivative of a function, which describes the rate at which a function changes. It is a core concept in calculus and is used to analyze various properties of functions, such as their slopes and curvatures. In the video, differentiation is performed to find the first and second derivatives of the given equation, which are essential for understanding the function's behavior.
Highlights

The problem presented is to find the second derivative of y with respect to x for the given equation y^2 - x^2 = 4.

Instead of solving for y and using traditional techniques, implicit differentiation is suggested as a more straightforward approach.

Implicit differentiation involves applying the chain rule to both sides of the equation, which is a key method for this problem.

The first step is to find the first derivative of y with respect to x, which is done by differentiating both sides of the equation.

The derivative of y^2 with respect to y is 2y, and by applying the chain rule, this becomes 2y * (dy/dx).

The derivative of x^2 with respect to x is 2x, and the derivative of a constant is zero.

The first derivative of y with respect to x is found to be (dy/dx) = x/y.

The next step is to find the second derivative by differentiating the expression for the first derivative with respect to x.

The quotient rule and the product rule are used to find the second derivative, which are essential calculus techniques.

The derivative of y with respect to x is rewritten as x * (y^(-1)), which simplifies the process of finding the second derivative.

The second derivative is found by applying the product rule to the expression x * (y^(-1)) and simplifying the result.

The final expression for the second derivative of y with respect to x is (d^2y/dx^2) = -x^2 / y^3.

The solution demonstrates the application of the chain rule, quotient rule, and product rule in calculus.

The problem-solving process showcases the importance of understanding the relationships between variables in an equation.

The method used can be applied to a variety of similar problems involving second derivatives.

The solution emphasizes the value of implicit differentiation in problems where variables are interdependent.

The process highlights the importance of step-by-step problem-solving and the application of fundamental calculus rules.

The final result is a clear demonstration of how to express the second derivative in terms of the original variables x and y.

Transcripts

Browse More Related Video

Implicit Differentiation (part 2)

Second Derivative of Implicit Function

Implicit Differentiation

Implicit Differentiation for Calculus - More Examples, #1

How to use implicit differentiation on an equation for dy dx

Implicit Differentiation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsCalculusImplicit DifferentiationDerivativesChain RuleQuotient RuleEducationTutorialInstructorMath Skills