How to Solve ANY Optimization Problem | Calculus 1
TLDRThe video script is an in-depth exploration of optimization problems using calculus. It guides viewers through three distinct examples, starting with maximizing the volume of an open-top box with a given surface area, followed by maximizing the area of a fenced-off rectangular region with a fixed perimeter, and concluding with finding the point on a parabola that is closest to a given point. The presenter outlines a five-step process for tackling such problems: identifying given quantities and desired outcomes, sketching the scenario, formulating primary and secondary equations, determining the feasible domain, and applying calculus to find maxima or minima. Each example is meticulously worked through to demonstrate the application of these steps, ultimately revealing the optimal solutions to the posed problems. The script emphasizes the utility of calculus in practical applications and encourages viewers to engage with the material through problem-solving.
Takeaways
- 📝 **Identify Given Quantities**: Begin by understanding the given constraints and what you are trying to optimize.
- 📈 **Sketch the Problem**: Visualize the situation, which helps in understanding and setting up the equations.
- 🧮 **Write Secondary Equations**: Formulate equations based on given information that isn't the quantity you're optimizing.
- 🔑 **Primary Equation**: Develop an equation for the quantity you're aiming to maximize or minimize.
- 🔗 **Relate Variables**: Use secondary equations to express the primary equation in terms of a single variable.
- 📐 **Determine Feasible Domain**: Establish the range of possible values for the variable that will produce a valid solution.
- 📉 **Apply Calculus**: Use calculus techniques such as derivatives to find critical points and endpoints for optimization.
- 🏁 **Check Endpoints and Critical Points**: Evaluate the function at endpoints and critical points to determine the maximum or minimum.
- 🔍 **Use Tests for Min/Max**: When necessary, apply the first or second derivative test to classify critical points.
- 📦 **Optimize Box Volume**: For a box with a given surface area, optimize volume by finding the correct dimensions.
- 🏞️ **Maximize Enclosed Area**: With a fixed perimeter, find the dimensions of a rectangle that maximize the enclosed area.
- 📐 **Minimize Distance to a Point**: On a curve, find the point that minimizes the distance to a given fixed point.
Q & A
What is the primary reason for discussing how to find maximums and minimums of functions?
-The primary reason is to solve optimization problems such as maximizing revenue, maximizing volume, minimizing surface area, etc., which are very useful in various real-world applications.
What is the first step in solving an optimization problem?
-The first step is to identify all given quantities and the quantities that are not known. If possible, make a sketch to visualize the problem.
What is a secondary equation in the context of optimization problems?
-A secondary equation is an equation for a quantity that is not the primary focus of optimization. It often provides a relationship between variables that can be used to express the primary equation in terms of a single variable.
What is the primary equation in optimization problems?
-The primary equation is the equation for the quantity that is being optimized, such as volume, area, or revenue.
How do you rewrite the primary equation in terms of a single variable?
-You use the secondary equation to express one of the variables in terms of the other. Then, substitute this expression into the primary equation to get an equation with a single independent variable.
What is the feasible domain in the context of optimization problems?
-The feasible domain refers to the set of possible values for the variables that satisfy the given constraints of the problem.
What is the extreme value theorem?
-The extreme value theorem states that a continuous function on a closed and bounded interval attains its maximum and minimum values at least once.
How do you find the maximum volume of an open-top box with a square base and a given surface area?
-First, express the volume in terms of a single variable using the given surface area. Then, find the critical points by taking the derivative and setting it to zero. Finally, evaluate the volume function at the critical points and endpoints to determine the maximum volume.
What is the process for finding the dimensions of a fenced-off rectangular field that borders a straight river and uses a given amount of fencing?
-Express the area in terms of a single variable using the total fencing available. Determine the feasible domain for the length of the rectangle. Use calculus to find the critical points within the domain. Apply the extreme value theorem to find the maximum area.
How do you find the point on a parabola that is closest to a given point?
-Express the distance between the point on the parabola and the given point as a function of a single variable. Use calculus to find the minimum distance by taking the derivative, setting it to zero, and solving for the variable.
What are the steps to solve optimization problems using calculus?
-The steps include: identifying given and unknown quantities, making a sketch, writing secondary and primary equations, reducing the primary equation to a single variable, determining the feasible domain, and using calculus to find the maximum or minimum value.
How can you support Wrath of Math on Patreon?
-You can support Wrath of Math on Patreon by providing financial support, which can give you early access to videos and access to PDF notes.
Outlines
📈 Optimization Problem Basics and Box Volume Maximization
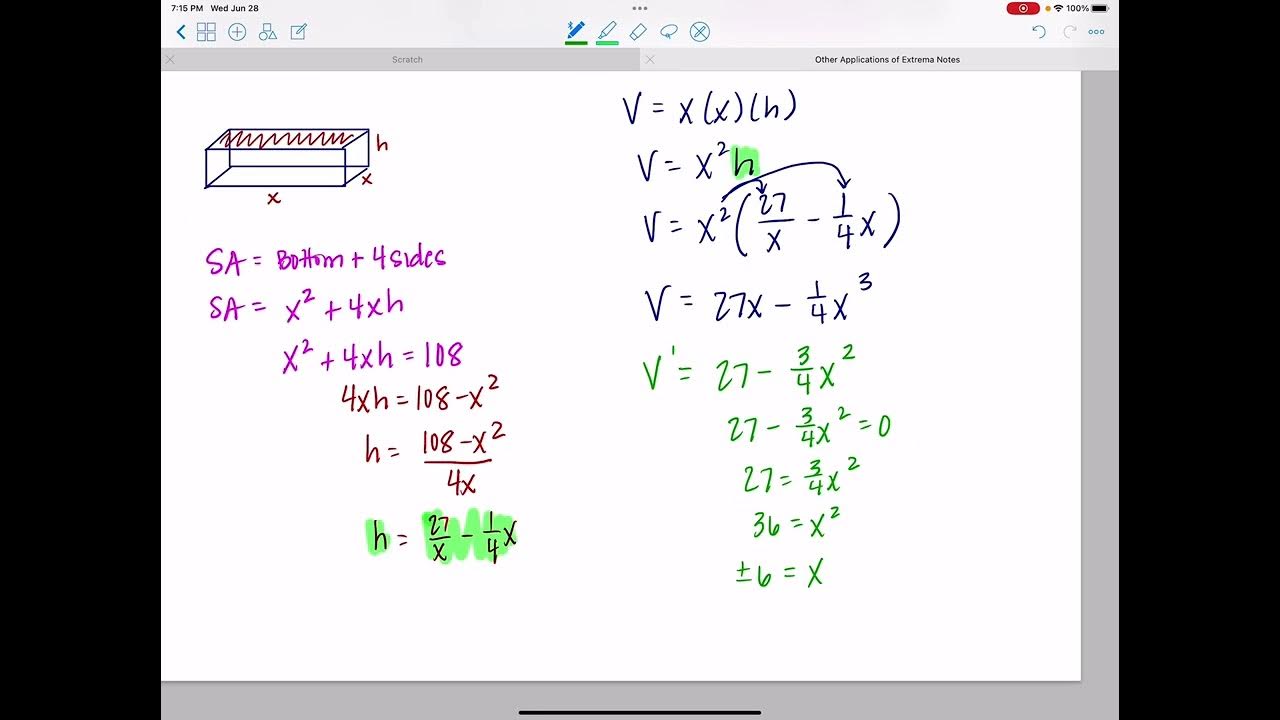
This paragraph introduces the concept of optimization problems, focusing on maximizing or minimizing certain quantities such as revenue, volume, or surface area. It outlines a step-by-step approach to solving these problems with three examples provided. The first example illustrates how to maximize the volume of an open-top box with a square base and a given surface area of 108 square inches. The process involves sketching the scenario, understanding given quantities, using these to form secondary and primary equations, and then applying calculus to find the optimal dimensions. The primary equation represents the volume, and the secondary equation represents the surface area restriction. By solving the secondary equation for one variable and substituting into the primary equation, we can apply calculus techniques to find the maximum volume, which in this case occurs when the box has dimensions of six by six by three inches.
🏡 Maximizing the Area of a Fenced Rectangular Field
The second paragraph presents an optimization problem where a farmer has 2,400 feet of fencing and wants to fence off a rectangular field bordering a straight river, requiring no fence along the river. The goal is to find the dimensions that maximize the area of the field. The problem begins with a sketch and identifies the given quantity (the total fencing available). A secondary equation representing the total fencing is set up, and then a primary equation for the area to be maximized is written. By expressing the primary equation in terms of a single variable using the secondary equation, the feasible domain for the variable is established. Applying calculus, specifically finding critical points and using the extreme value theorem, the optimal dimensions for the maximum area are determined to be 600 by 1200 feet, yielding an area of 720,000 square feet.
🔍 Finding the Point on a Parabola Closest to a Given Point
The third paragraph tackles a more complex optimization problem: finding the point on the parabola defined by y^2 = 2x that is closest to the point (1, 4). This involves minimizing the distance between a point on the parabola and the given point. The process starts with a sketch and the use of the parabola's equation as a secondary equation. The primary equation is the distance formula, which is then simplified using the parabola's equation to express distance in terms of a single variable. The domain of the function is all real numbers since there are no physical constraints on the variable y. To find the minimum distance, the square of the distance (D^2) is minimized instead of the distance itself, simplifying calculations. The derivative of this function is taken, and critical points are found by setting the derivative to zero. Using the first and second derivative tests, it is determined that a minimum exists at y = 2, which corresponds to an x-coordinate of 2 on the parabola, making the point (2, 2) the closest point to (1, 4) on the given parabola.
📝 Summary of Steps for Solving Optimization Problems
The final paragraph summarizes the steps for solving optimization problems as demonstrated in the previous examples. The steps include identifying given and unknown quantities, making a sketch, writing secondary equations based on the given information, writing a primary equation for the quantity to be optimized, reducing the primary equation to a single independent variable using the secondary equations, determining the feasible domain, and finally using calculus to find the maximum or minimum value. The paragraph emphasizes the consistency of this process across different types of optimization problems and encourages viewers to apply these steps to a variety of scenarios. It also provides information on further resources, including links to additional problems and calculus playlists, and mentions the option to support the content creator on Patreon for early access to videos and PDF notes.
Mindmap
Keywords
💡Optimization
💡Maximums and Minimums
💡Surface Area
💡Volume
💡Primary Equation
💡Secondary Equation
💡Feasible Domain
💡Derivative
💡Critical Points
💡Extreme Value Theorem
💡First and Second Derivative Tests
Highlights
The importance of finding maximums and minimums of functions is emphasized for solving optimization problems such as maximizing revenue, volume, or minimizing surface area.
A step-by-step approach to solving optimization problems is presented, which includes three examples.
The first example involves maximizing the volume of an open-top box with a given surface area.
The second example focuses on maximizing the area of a fenced-off region with a fixed amount of fencing, using the river as one boundary.
The third example is more complex, aiming to find the point on a parabola that minimizes the distance to a given point.
The process of optimization involves five key steps: identifying given quantities, writing secondary and primary equations, reducing to a single variable, determining the feasible domain, and applying calculus to find the optimum.
In the open-top box problem, the volume is maximized when the box dimensions are six by six by three, given a surface area of 108 square inches.
For the fenced-off region, the maximum area is achieved with dimensions of 600 by 1200 feet using 2400 feet of fencing.
The point on the parabola y^2 = 2x that is closest to the point (1, 4) is found to be (2, 2).
The primary equation represents the quantity to be optimized, while the secondary equation represents a given restriction.
The feasible domain for the primary equation is crucial in determining the range of possible values for the variable.
The extreme value theorem is used when the domain is a closed interval to find the maximum or minimum of a function.
Derivatives play a key role in finding critical points, which are potential candidates for maximums or minimums.
The first and second derivative tests are used to classify critical points when the domain is not a closed interval.
The method of optimization using calculus can be applied to a wide range of practical problems, from geometry to economics.
The video provides a comprehensive guide to using calculus for optimization, including detailed examples and mathematical reasoning.
Support for the Wrath of Math channel on Patreon is encouraged for early access to videos and additional resources.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: