Calculus | Derivatives of a Function - Lesson 7 | Don't Memorise
TLDRThe video script delves into the concept of 'steepness', illustrating how the difficulty of climbing a mountain like K2 surpasses Everest due to factors beyond height, such as steepness. It explains steepness through the ratio of vertical to horizontal lengths, and how this ratio signifies the vertical distance covered relative to the horizontal distance. The script then transitions into the idea of slope, which is the measure of steepness for a line, and is related to the tangent function in trigonometry. The concept of a derivative is introduced, linking it to the rate of change of a function and how it corresponds to the slope of a curve at a given point. The video uses the analogy of the Earth's curvature to explain how a curve can be approximated by a tangent line, which is a straight line that touches the curve at a single point. The script further explores the idea that the slope of this tangent line at any point on a curve represents the instantaneous rate of change of the function at that point. It concludes by explaining that differentiation is the process used to find the instantaneous rate of change, or the derivative, which is denoted as 'D Y by D X'. The video promises to explore how to calculate derivatives and their intuitive meaning in future lessons.
Takeaways
- 🏔️ The hardest mountain to climb is not Mount Everest, but K2, due to its steepness and other challenging factors.
- 📏 Steepness is a critical factor in climbing difficulty and is measured by the ratio of vertical to horizontal distance.
- 📐 The concept of slope is used to quantify the steepness of a line, which is the ratio of the vertical change to the horizontal change.
- 📈 The slope of a line is also related to the trigonometric tangent function, where the slope equals tan(θ).
- 🤔 The idea of a curve's slope being variable across different points introduces the need to consider the slope at a specific point.
- 🌐 The concept of a tangent line is introduced as a way to approximate the curve locally with a straight line at a given point.
- 📉 The instantaneous rate of change of a function at a specific point is equivalent to the slope of the tangent line at that point.
- 🔄 Differentiation is a mathematical process that helps us find the instantaneous rate of change or the slope of the tangent line.
- 📌 The rate of change of a function, particularly in the context of motion, corresponds to the concept of speed or velocity.
- ⏱️ As the time interval approaches zero, the average rate of change approaches the instantaneous rate of change.
- 🧮 The derivative of a function at a point is defined as the instantaneous rate of change at that point and is denoted by 'dY/dx'.
Q & A
Which mountain is considered the hardest to climb, and why is it more challenging than Mount Everest?
-The hardest mountain to climb is K2, the second highest mountain in the world. It is considered more challenging than Mount Everest due to factors beyond height, such as steepness, which makes the ascent more difficult.
What is meant by the term 'steepness' in the context of climbing mountains?
-Steepness refers to the incline or gradient of a mountain's slope. A steeper mountain is harder to climb because it requires more vertical ascent for a given horizontal distance.
How can one measure the steepness of a straight line?
-The steepness of a straight line can be measured by calculating the ratio of the vertical length to the horizontal length. A higher ratio indicates a steeper line.
What is the relationship between the steepness of a line and the angle it makes with the horizontal?
-The steepness of a line is related to the angle it makes with the horizontal through the trigonometric tangent function. The greater the angle, the steeper the line, and the higher the value of the tangent of that angle.
How does the concept of a derivative relate to the slope of a curve at a specific point?
-The derivative of a function at a specific point represents the instantaneous rate of change at that point, which is equivalent to the slope of the tangent line to the curve at that point.
What is the significance of the tangent line to a curve at a particular point?
-The tangent line at a particular point on a curve provides a linear approximation of the curve near that point. Its slope represents the instantaneous rate of change of the function at that point.
How does the concept of differentiation help in understanding the slope of a curve?
-Differentiation allows us to find the derivative of a function, which is the instantaneous rate of change. This rate of change corresponds to the slope of the tangent line to the curve at a given point, thus helping us understand the varying steepness along the curve.
What is the difference between average speed and instantaneous speed?
-Average speed is the total distance traveled divided by the total time taken, calculated over a certain time interval. Instantaneous speed, on the other hand, is the speed of an object at a specific moment in time, which is the limit of the average speed as the time interval approaches zero.
How is the slope of a tangent line related to the rate of change of a function?
-The slope of the tangent line at a point on a curve is equal to the rate of change of the function at that point. It represents how quickly the value of the function changes with respect to changes in the input variable.
What is the derivative of a function, and how is it denoted?
-The derivative of a function at a particular value of 'X' is its instantaneous rate of change at that point. It is usually denoted by 'dY/dX' or 'DY by DX'.
Why is the process of finding the limit as 'delta X' tends to zero important in calculus?
-Finding the limit as 'delta X' tends to zero is crucial because it allows us to determine the instantaneous rate of change of a function. This process transforms the concept of average rate of change into the instantaneous rate of change, which is the definition of the derivative.
How does the concept of a derivative help in understanding the behavior of a function near a specific point?
-The derivative provides a measure of how a function is changing at a specific point. It allows us to understand the function's behavior, such as whether it is increasing or decreasing, and at what rate, which is valuable for making predictions and analyzing the function's local properties.
Outlines
🗻 Understanding Mountain Steepness and the Concept of Slope
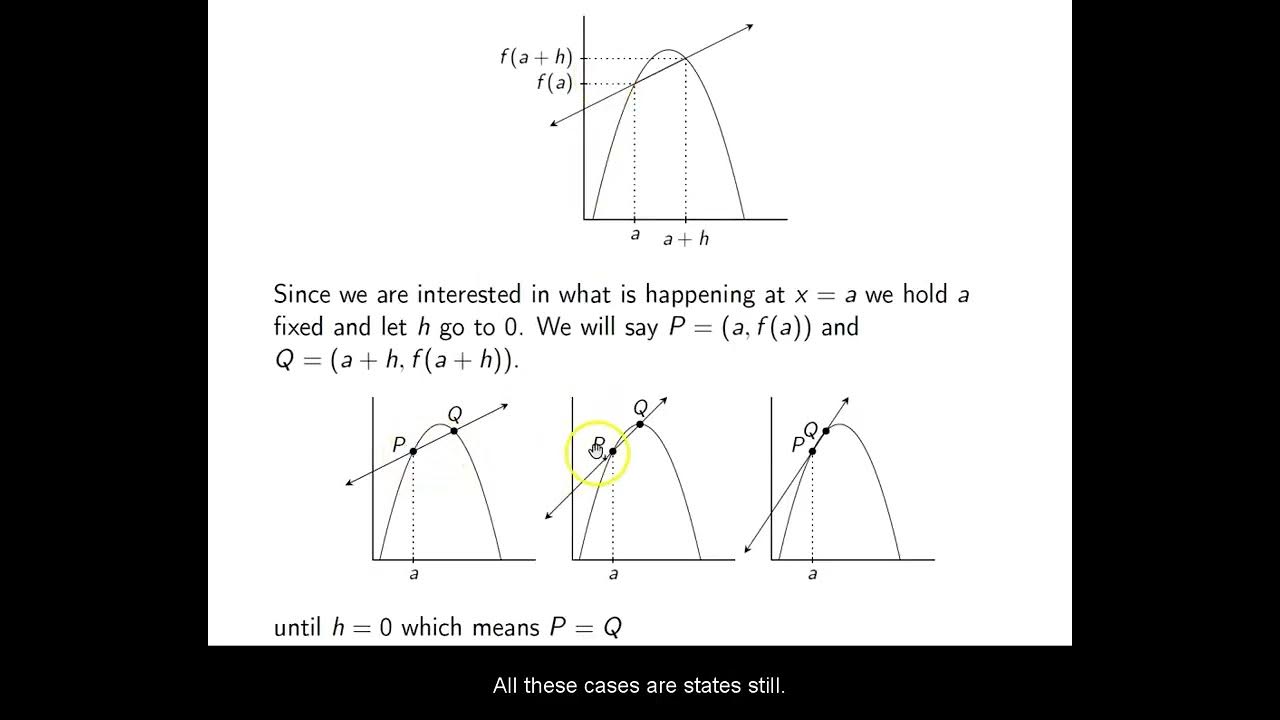
The first paragraph introduces the concept of mountain climbing difficulty, contrasting the commonly perceived hardest mountain, Mount Everest, with the actual hardest to climb, K2, known as the 'Savage Mountain'. It explains that factors beyond height, such as steepness, contribute to the difficulty. The paragraph uses the analogy of two mountains to illustrate steepness and then transitions to a mathematical explanation using ratios of vertical to horizontal lengths to quantify steepness. It introduces the concept of slope as a measure of steepness and relates it to the tangent function in trigonometry. The paragraph concludes with an introduction to differentiation and how it can be used to understand the varying steepness of a curve, particularly at a specific point 'P', by approximating the curve with a tangent line.
📈 The Rate of Change and Instantaneous Speed through Differentiation
The second paragraph delves into the importance of finding the slope of the tangent line at a point on a curve, which represents the instantaneous rate of change of a function at that point. It explains the concept of a function and how the change in one variable ('X') affects another ('Y'), using the ratio 'delta Y over delta X'. This ratio is shown to be related to the slope of a line representing the function's graph. The paragraph further explores how the slope of a curve at a point reflects the rate of change at that point and how this can be understood through the tangent line. It uses the example of an object's distance traveled over time to illustrate how the rate of change corresponds to speed. The concept of the instantaneous rate of change, or the instantaneous speed, is introduced and related to the process of differentiation, which is used to find the instantaneous speed at a specific point 'P' by considering the average speed over an interval that approaches zero.
🧮 Approaching the Derivative and Instantaneous Rate of Change
The third paragraph focuses on the process of finding the instantaneous rate of change, or the derivative, of a function. It explains that as the time interval 'delta X' approaches zero, the average speed converges to the instantaneous speed, which is the instantaneous rate of change at a specific point 'X not'. The paragraph illustrates how the secant line, representing the average rate of change over an interval, approaches the tangent line as 'delta X' decreases, thus becoming a measure of the instantaneous rate of change. The concept of the derivative is introduced as a formalization of this rate of change, denoted by 'D Y by D X'. The paragraph concludes with a teaser for the next lesson, which will explore how to calculate derivatives and understand their intuitive meaning.
Mindmap
Keywords
💡Mount Everest
💡K2
💡Steepness
💡Slope
💡Tangent Line
💡Derivative
💡Instantaneous Rate of Change
💡Differentiation
💡Secant Line
💡Rate of Change
💡Trigonometric Tangent
Highlights
Mount Everest is not the hardest mountain to climb; K2 is considered more challenging due to its steepness and other factors.
Steepness is a critical factor in determining the difficulty of climbing a mountain.
The ratio of vertical to horizontal length can be used to measure the steepness of a line or slope.
The steeper a line, the greater the angle it forms and the higher its tangent value.
Differentiation is key to understanding the slope of a curve, which is related to the derivative of a function.
The slope of a curve at a point is equal to the slope of the tangent line at that point.
A curve can be approximated by a tangent line in a very small region around a point on the curve.
The concept of a tangent line is fundamental to calculus, as it allows for the approximation of a curve with a straight line.
The rate of change in a function is related to the slope of the curve representing the function.
For a straight line, the rate of change is constant, whereas for a curve, it varies depending on the point.
The instantaneous rate of change of a function at a particular value of X is called the instantaneous speed or the derivative at that point.
The process of finding the instantaneous speed involves using differentiation and considering limits as the time interval approaches zero.
The average rate of change between two points on a curve is equal to the slope of the secant line between those points.
As the time interval approaches zero, the secant line approaches the tangent line, allowing for the calculation of the instantaneous rate of change.
The derivative of a function at a particular value of X is denoted by 'DY/DX' and represents the instantaneous rate of change at that point.
The concept of derivatives is essential for understanding the rate of change in various real-world applications, such as calculating the speed of an object in motion.
The video concludes with a teaser for the next lesson, which will delve deeper into the concept of derivatives and their practical applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: