Area between two curves (using a calculator) - AP Calculus

vinteachesmath
4 Mar 202007:52
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Vincent demonstrates how to calculate the area between two curves using technology. He introduces the functions f(x) = ln(x-1)+5 and g(x) = x+2, and guides viewers through graphing them to find their intersection points. Vincent explains the concept of cross-sections and rectangles to represent the area, emphasizing the importance of identifying the limits of integration, a and b. Utilizing a calculator, he shows the process of setting up and solving the integral of (f(x) - g(x)) from a to b, resulting in an area of 1.949 square units. The video concludes with a call to action for likes and subscriptions, encouraging viewers to engage with the content.

Takeaways
  • πŸ“š The video is a tutorial on finding the area between two curves using technology.
  • πŸ“ˆ The functions given are f(x) = ln(x - 1) + 5 and g(x) = x + 2, which are graphed to visualize their intersection.
  • πŸ” The intersection points of the curves are crucial for determining the limits of integration.
  • πŸ“ The concept of area between curves is explained using the idea of infinitely thin rectangles or cross-sections.
  • πŸ“‰ The area between the curves is calculated by subtracting the lower function (g(x)) from the upper function (f(x)) for each small segment.
  • βš™οΈ The area calculation involves setting up an integral from point A to point B, where A and B are the x-values of the intersection points.
  • πŸ“ The process of finding A and B is demonstrated using a calculator's trace and intersection features.
  • πŸ’‘ A helpful tip is given for storing the values of A and B in the calculator for easy recall during calculations.
  • 🧩 The integral set up is f(x) - g(x) dx from A to B, representing the sum of all infinitely small rectangles.
  • πŸ”’ The final step involves entering the functions and limits into the calculator to compute the area.
  • πŸ“Š The result of the area calculation is presented, rounded to three decimal places as per AP exam standards.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is to demonstrate how to find the area between two curves using technology.

  • What are the two functions given in the video?

    -The two functions given in the video are f(x) = ln(x - 1) + 5 and g(x) = x + 2.

  • How does the video suggest to graph the functions?

    -The video suggests to graph the functions by setting the X minimum to zero, X maximum to 10, and adjusting the Y values to range from Y minimum zero to Y maximum ten.

  • What is the concept of finding the area between curves in the video?

    -The concept involves cross sections on the XY plane, which are represented as infinitely thin rectangles (Delta X), and the height is determined by the difference between the functions f(x) and g(x).

  • How is the area of a rectangle related to the area between the curves?

    -The area of a rectangle is base times height, which in this context is represented by f(x) - g(x) times Delta X, giving a small slice of the total area between the curves.

  • What is the mathematical representation for the area between the curves?

    -The area between the curves is represented by the integral from A to B of f(x) - g(x) dx, where A and B are the x-values of the intersection points of the curves.

  • How does the video describe finding the values of A and B?

    -The values of A and B are found by tracing the intersection points of the two curves on the graph using the technology provided.

  • What is a trick mentioned in the video for storing the values of A and B?

    -The trick mentioned is to press 2nd mode to quit the screen, then press store, and store the answer as the letter A or B, so that anytime the letter is written, the stored value will appear.

  • How does the video describe the final step of calculating the area using the calculator?

    -The final step involves using the integral function on the calculator, inputting the values for A and B, the functions f(x) and g(x), and then pressing enter to calculate the area.

  • What is the final calculated area between the curves in the video?

    -The final calculated area between the curves is 1.9 square units.

  • What does the video suggest for rounding the final answer?

    -The video suggests rounding the final answer to three decimal places, as preferred by the AP test.

Outlines
00:00
πŸ“š Introduction to Finding Area Between Curves

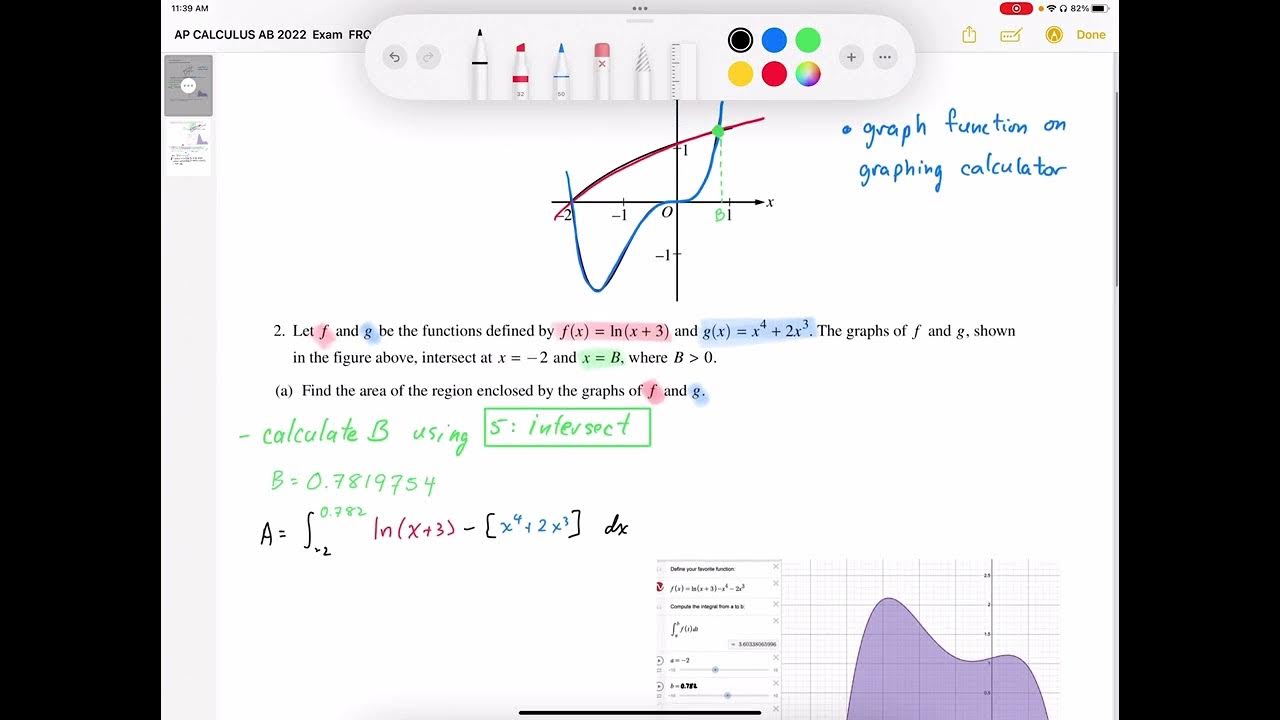
Vincent introduces a tutorial on calculating the area between two curves using technology. The functions f(x) = ln(x) - 1 + 5 and g(x) = x + 2 are graphed, and the intersection in the first quadrant is identified. The viewer is guided to set the graph's x-axis range from 0 to 10 and y-axis from 0 to 10 for clarity. The concept of finding the area between curves is explained through the idea of infinitesimally thin rectangles, or 'slices', represented by the function f(x) - g(x). The integral formula for the area A from x = a to x = b is introduced, where a and b are the x-coordinates of the intersection points.

05:01
πŸ” Locating Intersection Points and Calculating the Area

The process continues with identifying the exact x-coordinates of the intersection points, which are crucial for determining the limits of integration. Using a calculator's intersection tracing feature, the coordinates for a and b are found to be approximately 1.5859434 and 4.1411932, respectively. These values are stored for easy reference in subsequent calculations. The integral of f(x) - g(x) from a to b is set up on the calculator, with the functions and limits of integration being inputted using stored values and shortcuts. The final area calculation yields a result of approximately 1.9 units, rounded to three decimal places as per AP exam standards. The video concludes with a prompt for viewers to like, subscribe, and leave comments if they have any requests.

Mindmap
Keywords
πŸ’‘Area between curves
The term 'area between curves' refers to the space enclosed by two intersecting curves on a graph. In the video's context, the area between the natural log curve and the linear function is the focus. The script explains how to calculate this area using integration, which is a fundamental concept in calculus. The video demonstrates the process of finding where the curves intersect to determine the limits of integration, which is essential for calculating the enclosed area.
πŸ’‘Natural log curve
A 'natural log curve' is a graphical representation of the natural logarithm function, ln(x). In the script, the natural log curve is one of the two functions being analyzed, specifically ln(x - 1) + 5. The video uses this curve to illustrate how to graph functions and find the area between them, emphasizing the importance of understanding the shape and behavior of different types of curves.
πŸ’‘Linear function
A 'linear function' is a function of the form f(x) = mx + b, where m and b are constants, and x is the variable. In the video, the linear function is G(x) = x + 2. The script uses this function to demonstrate how to graph a straight line and how it intersects with the natural log curve, which is crucial for determining the boundaries of the area to be calculated.
πŸ’‘Graphing
Graphing is the process of plotting the graph of a mathematical function, showing the relationship between variables. The script describes how to graph the functions f(x) and G(x) using technology, setting the stage for visualizing the area between the curves. The video emphasizes the importance of graphing as a preliminary step before attempting to calculate areas or solve other problems involving functions.
πŸ’‘Integration
Integration is a mathematical concept used to calculate the area under a curve between two points. In the script, integration is the method used to find the area between the natural log curve and the linear function. The video explains that the area can be found by summing infinitely small rectangles, represented by the integral of f(x) - G(x) from a to b, where a and b are the x-coordinates of the intersection points.
πŸ’‘Riemann sum
A 'Riemann sum' is a method used in calculus to approximate the area under a curve by summing the areas of rectangles. The script mentions the Riemann sum concept as a way to understand the process of finding the area between two curves through integration. The video uses this concept to explain how the sum of all infinitely small rectangles (or slices) can be used to approximate the total area.
πŸ’‘Intersection point
An 'intersection point' is the point where two curves on a graph meet. The script describes how to find the intersection points of the natural log curve and the linear function by tracing on a graphing calculator. These points are essential as they provide the limits of integration (a and b) for calculating the area between the curves.
πŸ’‘Delta X
In the context of the video, 'Delta X' represents a small change in the x-direction, used to define the width of an infinitely thin rectangle in the cross-section of the area to be calculated. The script explains that the area of each rectangle (or slice) is given by the base times height, where the base is represented by Delta X and the height by the difference in the function values, f(x) - G(x).
πŸ’‘Technology
The term 'technology' in the script refers to the use of a graphing calculator or software to assist in mathematical calculations and visualizations. The video demonstrates how to use technology to graph functions, find intersection points, and calculate areas between curves, emphasizing the utility of technology in simplifying complex mathematical tasks.
πŸ’‘Integral
An 'integral' is a mathematical concept that represents the process of integration. In the script, the integral is used to express the sum of all the infinitely small rectangles that make up the area between the curves. The video shows how to set up the integral from a to b of f(x) - G(x) to find the exact area, highlighting the integral as a fundamental tool in calculus for area calculations.
Highlights

Introduction to finding the area between two curves using technology.

Graphing the functions f(x) = ln(x - 1) + 5 and g(x) = x + 2.

Setting the x-axis range from 0 to 10 and y-axis from 0 to 10 for clarity.

Understanding the concept of cross-sections and the role of Delta X.

Modeling the cross-section as f(x) - g(x) for the area calculation.

The area of a rectangle representing a small slice of the total area.

Defining the area 'a' and its representation as a Riemann sum.

Determining the limits of integration, points A and B, by tracing intersection points.

Storing intersection points as A and B for later use in calculations.

Using technology to set up the integral for area calculation.

Shortcuts for entering functions f(x) and g(x) into the calculator.

Calculating the integral from A to B of f(x) - g(x).

The importance of rounding the result to three decimal places as per AP exam standards.

Final calculation of the area between the curves resulting in 1.904 units.

Conclusion and invitation for feedback, likes, and subscriptions.

Transcripts

Browse More Related Video

Area Between Two Curves

2013 AP Calculus AB Free Response #5

2022 AP Calculus AB Free Response #2

2015 AP Calculus AB Free Response #2

AP CALCULUS AB 2022 Exam Full Solution FRQ#2a

2008 AP Calculus AB Free Response #1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Area CalculationCurve AnalysisMath TutorialIntegralsGraphingTechnologyEducationalCalculusGeometryVincent's Video