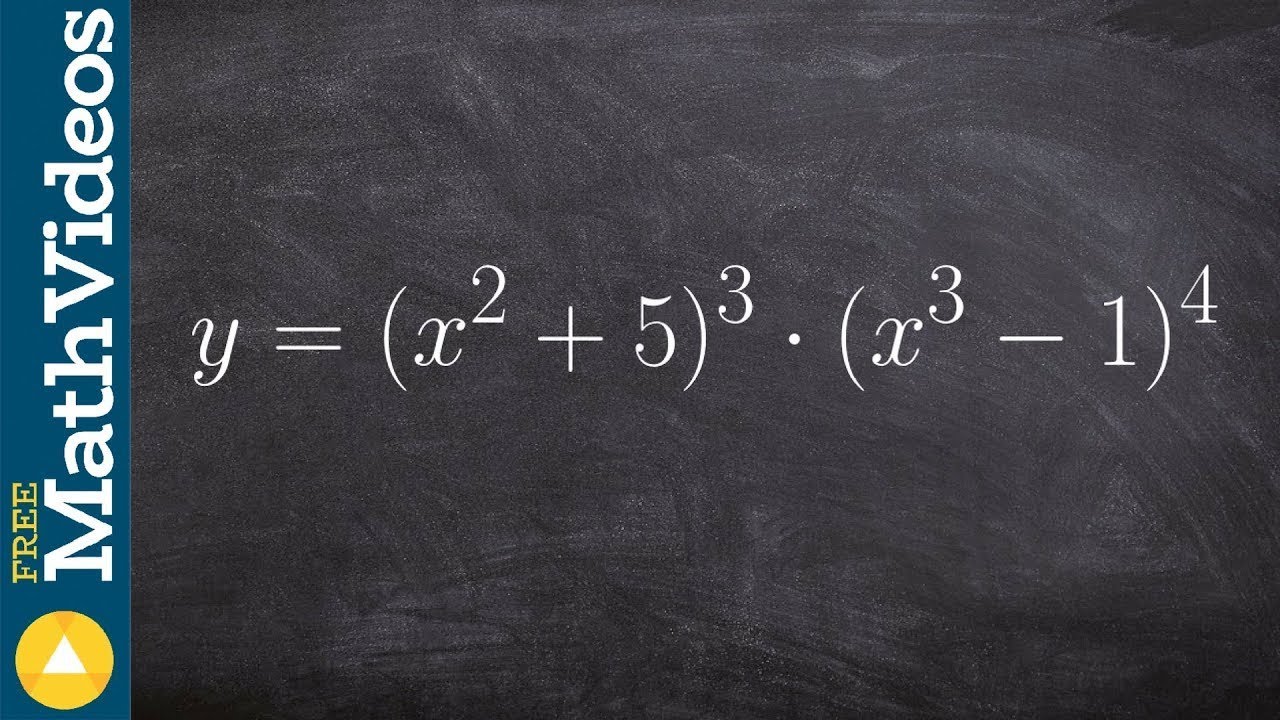Product Rule for Derivatives

Professor Monte

9 Jun 202005:02

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Professor Monte introduces the concept of the product rule for derivatives in calculus. He begins by explaining the formula for the product rule, which is the first function times the derivative of the second plus the second function times the derivative of the first. To illustrate the rule's application, he provides two examples. The first example involves the function x squared times x to the sixth, which simplifies to x to the eighth, and its derivative is calculated to be 8x to the seventh. The second example is more complex, involving x squared times 5x minus 2, and the derivative is found to be 15x squared minus 4x. Professor Monte emphasizes the importance of practicing the product rule and encourages viewers to subscribe for more educational content. He also invites suggestions for future problem-solving videos in the comments section.

Takeaways

📚 The Product Rule for derivatives is a fundamental concept in calculus, used to find the derivative of a product of two functions.
🔢 The formula for the Product Rule is: (first function) * (derivative of second function) + (second function) * (derivative of first function).
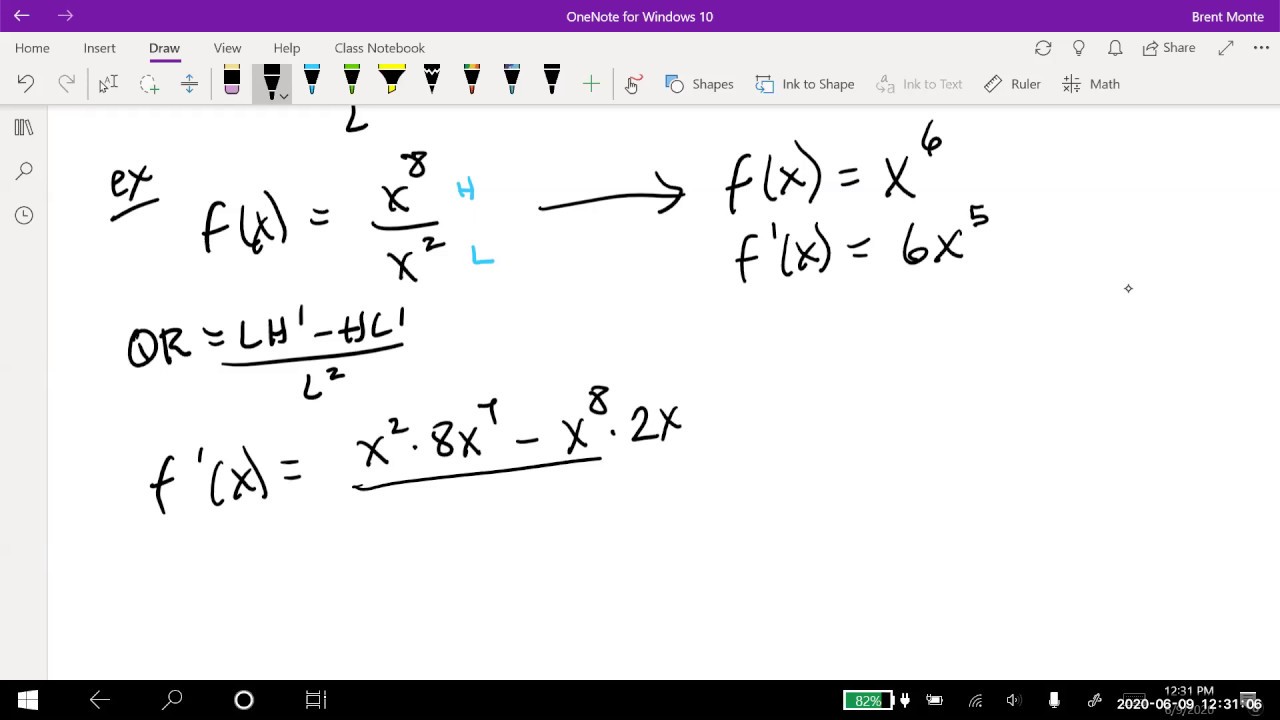
📈 An example given in the script is (x^2) * (x^6), which simplifies to x^8, and its derivative, using the product rule, is 8x^7.
🧮 The script demonstrates the process of applying the Product Rule step by step, emphasizing the importance of understanding the order of operations.
✍️ It's important to write down the Product Rule formula regularly to reinforce memory and understanding.
🤔 The script suggests that while the Product Rule can be straightforward in some cases, it becomes essential when dealing with more complex functions like e^x or ln(x).
📝 For the function x^2 * (5x - 2), the derivative is found by applying the Product Rule, resulting in 15x^2 - 4x.
🔁 The Product Rule can be written in a different order due to the commutative properties of multiplication and addition, but the mathematical result remains the same.
📉 When cleaning up the expression after applying the Product Rule, like terms should be combined to simplify the derivative.
📚 The script encourages practice with the Product Rule to gain proficiency and understanding.
📺 The speaker invites viewers to subscribe to their channel for more educational content.
✉️ The script ends with an invitation for viewers to comment with suggestions for other problems they would like to see covered in future videos.

Q & A

What is the product rule for derivatives?
-The product rule for derivatives states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. Mathematically, it is expressed as (fg)' = f'g + fg'.
What is the first step in applying the product rule to find the derivative of a function?
-The first step is to identify the two functions being multiplied together, label them as 'f' and 'g', and then apply the formula by calculating the derivative of 'f' and 'g' separately.
In the example provided, what are the two functions being multiplied together?
-In the example, the two functions being multiplied are f(x) = x^2 and g(x) = x^6.
What is the expected derivative of x^8 using the power rule?
-Using the power rule, the derivative of x^8 is 8x^7.
How does the product rule confirm the derivative of x^2 times x^6?
-The product rule breaks down the derivative into two parts: the derivative of the first function (x^2) times the second function (x^6) and the first function (x^2) times the derivative of the second function (6x^5). After simplifying, it results in 6x^7 + 2x^7, which combines to 8x^7, confirming the expected derivative.
What is the second example function provided in the script?
-The second example function is H(x) = x^2 * (5x - 2).
How does the product rule help in finding the derivative of a more complex function like H(x) = x^2 * (5x - 2)?
-The product rule allows us to find the derivative by multiplying the derivative of the first function (x^2) by the second function (5x - 2) and adding it to the product of the first function (x^2) and the derivative of the second function (5). This results in a derivative of 5x^2 + 10x - 4x, which simplifies to 15x^2 - 4x.
Why is it important to practice the product rule?
-Practicing the product rule is important because it is a fundamental technique used in calculus to find derivatives of products of functions, especially when the functions are not easily simplified or involve more complex operations like exponentials or logarithms.
Can the order of the functions in the product rule be switched?
-Yes, the order of the functions can be switched in the product rule because multiplication and addition are commutative operations. However, when switching the order, ensure that you also switch which function's derivative is being multiplied by the other function.
What is the advantage of writing down the product rule formula periodically?
-Writing down the product rule formula periodically helps to reinforce memory and ensures that the formula is accurately applied, especially when dealing with more complex problems or when the rule is used repeatedly.
What is the final answer for the derivative of H(x) = x^2 * (5x - 2) using the product rule?
-The final answer for the derivative of H(x) using the product rule is H'(x) = 15x^2 - 4x.
Why might one not always be able to use the power rule to find the derivative?
-One might not always be able to use the power rule to find the derivative when the function involves factors that are not simple powers of x, such as e^x, ln(x), or when a chain rule is required for more complex expressions.

Outlines

00:00

📚 Introduction to the Product Rule for Derivatives

Professor Monte begins the video by introducing the topic of the product rule for derivatives. He explains that for a product of two functions, P(x) = f(x) * g(x), the derivative P'(x) is found by multiplying the first function by the derivative of the second and adding it to the second function times the derivative of the first, expressed as (first * derivative of second) + (second * derivative of first). He emphasizes the importance of remembering this formula for the examples that follow.

Mindmap

Keywords

💡Product Rule

The Product Rule is a fundamental theorem in calculus that allows for the differentiation of a product of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the video, Professor Monte uses the Product Rule to find the derivatives of various functions, emphasizing its importance in calculus.

💡Derivatives

Derivatives are a measure of how a function changes as its input changes. They are a central concept in calculus and are used to analyze rates of change and to find the slopes of tangents to curves at specific points. In the script, Professor Monte discusses derivatives in the context of applying the Product Rule to find the rate of change of a product of two functions.

💡Functions

In mathematics, a function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. An example from the script is 'f of X' and 'G of X', which are used to represent two different mathematical functions that are being multiplied together.

💡Exponents

Exponents are a mathematical notation indicating the number of times a base number is multiplied by itself. In the context of the video, when dealing with functions like 'x squared' or 'X to the sixth', exponents are crucial for understanding how to apply the Product Rule correctly and simplify the resulting expression, as seen when adding '6x to the seventh' and '2x to the seventh'.

💡Power Rule

The Power Rule is a basic rule in calculus that allows for the differentiation of power functions. It states that the derivative of x to the n (where n is a constant) is n times x to the n minus one. In the video, Professor Monte mentions the Power Rule in passing, noting that it can be used in some cases instead of the Product Rule when the functions being differentiated are simpler.

💡Chain Rule

The Chain Rule is another important theorem in calculus used to compute the derivative of a composition of functions. Although not the main focus of the video, Professor Monte alludes to the Chain Rule when mentioning functions like 'e to the X' or 'Ln of X', indicating that it would be necessary for more complex functions that cannot be differentiated using just the Product Rule.

💡Like Terms

Like Terms are terms in a mathematical expression that have the same variables raised to the same powers. When differentiating using the Product Rule, terms may be generated that are like terms, and they can be combined by adding their coefficients. In the script, Professor Monte combines '6x to the seventh' and '2x to the seventh' to form '8x to the seventh'.

💡Distributive Property

The Distributive Property is a fundamental property in algebra that allows for the distribution of multiplication over addition or subtraction. In the context of the video, when Professor Monte deals with the function 'x squared times 5x minus 2', he uses the Distributive Property to expand the expression before applying the Product Rule.

💡Combining Like Terms

Combining Like Terms is the process of adding or subtracting coefficients of like terms in a mathematical expression to simplify the expression. In the video, after applying the Product Rule to 'x squared times 5x minus 2', Professor Monte combines '5x squared' and '10x squared' to get '15x squared', demonstrating this process.

💡Coefficients

In algebra, coefficients are the numerical factors in a term. They multiply the variables in a term to give the term its value. When Professor Monte applies the Product Rule, he encounters terms with coefficients, such as '5x squared' and '10x squared', which are then combined to form '15x squared'.

💡Practice

Practice is the act of performing or working at a task to improve or to make熟练 (proficient). Throughout the video, Professor Monte emphasizes the importance of practicing the Product Rule to gain proficiency in differentiating products of functions. He encourages viewers to apply what they've learned through practice to solidify their understanding.

Highlights

Professor Monte introduces the product rule for derivatives.

The product rule is expressed as the first function times the derivative of the second plus the second times the derivative of the first.

An example is given with the function x^2 times x^6, which simplifies to x^8.

The derivative of the example function is calculated to be 8x^7, confirming the product rule's validity.

The importance of the product rule when the power rule is not applicable is emphasized.

A second, more complex example is introduced with the function x^2 times (5x - 2).

The product rule is applied to the second example, demonstrating its general use.

The derivative of the second example is calculated to be 15x^2 - 4x.

The process of distributing and combining like terms is shown in detail.

The video encourages viewers to practice the product rule to gain proficiency.

The video provides an invitation to subscribe to Professor Monte's channel for more educational content.

Suggestions for other problems to cover in future videos are welcomed in the comments.

The video concludes with a reminder that practice is key to mastering the product rule.

The video emphasizes the simplicity of the product rule once it is practiced.

The product rule is applicable when dealing with functions such as e^x or ln(x) where a chain rule might be involved.

The video demonstrates the use of the product rule in a step-by-step manner, making it accessible for learners.

The video highlights the commutative property of multiplication and addition in the context of the product rule.

The video provides a clear explanation of how to handle the derivative of each function in the product.

Transcripts

Browse More Related Video

Product Rule For Derivatives

Taking the derivative of two binomials using product and chain rule

Math 1325 Lecture 9 5 - Product & Quotient Rule

Quotient Rule for Derivatives

Product rule proof | Taking derivatives | Differential Calculus | Khan Academy

Simplifying Derivatives

Product Rule for Derivatives

Takeaways

Q & A

What is the product rule for derivatives?

What is the first step in applying the product rule to find the derivative of a function?

In the example provided, what are the two functions being multiplied together?

What is the expected derivative of x^8 using the power rule?

How does the product rule confirm the derivative of x^2 times x^6?

What is the second example function provided in the script?

How does the product rule help in finding the derivative of a more complex function like H(x) = x^2 * (5x - 2)?

Why is it important to practice the product rule?

Can the order of the functions in the product rule be switched?

What is the advantage of writing down the product rule formula periodically?

What is the final answer for the derivative of H(x) = x^2 * (5x - 2) using the product rule?

Why might one not always be able to use the power rule to find the derivative?