Product Rule For Derivatives

The Organic Chemistry Tutor
24 Feb 201811:11
EducationalLearning
32 Likes 10 Comments

TLDRThis video lesson explains the product rule for derivatives, a fundamental concept in calculus. The rule states that the derivative of a product of two functions is the derivative of the first function times the second function, plus the first function times the derivative of the second function. The video provides several examples to illustrate the rule, including the derivative of x squared times sine x and more complex expressions involving multiple functions. It also demonstrates how to apply the product rule when dealing with three or more factors in a product. The lesson is practical, clear, and informative, making it an excellent resource for anyone studying calculus.

Takeaways
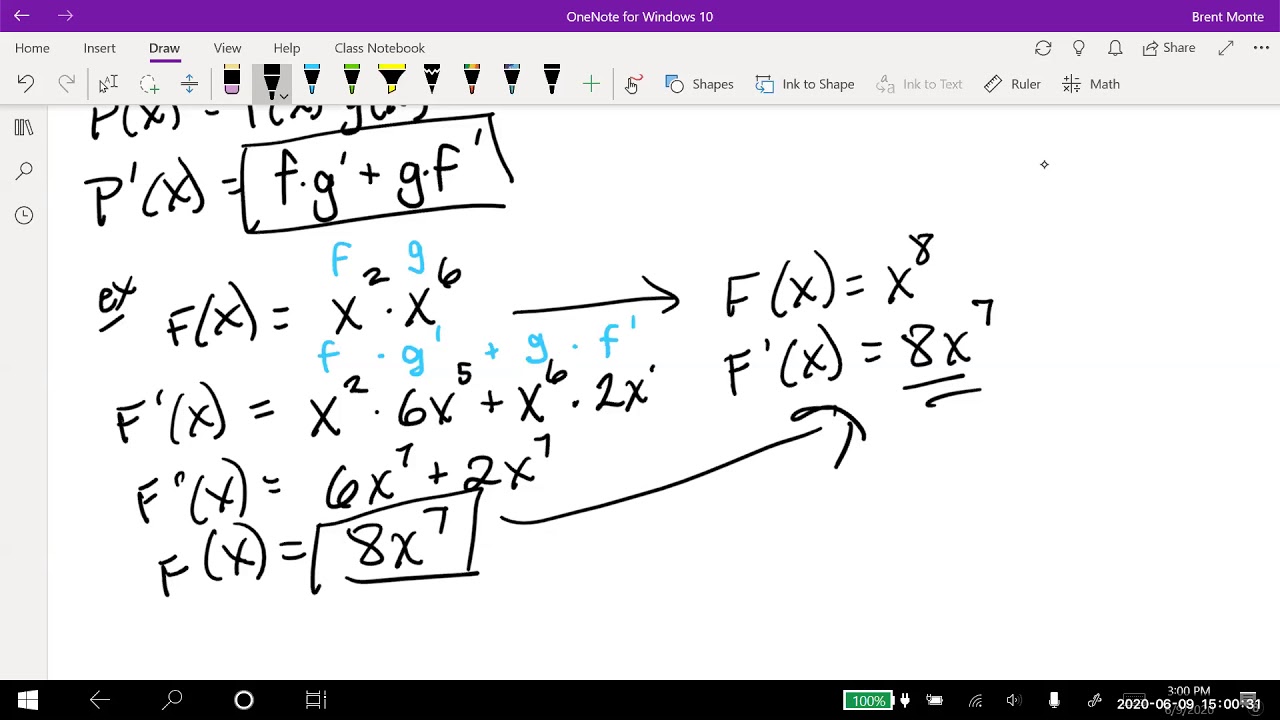
  • 📚 The Product Rule for derivatives states that the derivative of a product of two functions (f*g) is f'*g + f*g'.
  • 🌟 Example: The derivative of x^2 * sin(x) is 2x*sin(x) + x^2*cos(x) after applying the product rule and simplifying.
  • 🔢 For the expression (5x - 9x^3) * (8 + x^2), the derivative is found by applying the product rule separately to each term and then combining them.
  • 📈 When differentiating 4*sin(x)*tan(x), the derivative of the first part is 4*cos(x) and the second part is sec^2(x), resulting in 4*sin(x)*sec^2(x) + 1 + sec^2(x).
  • 🌠 If a function has more than two terms, like (x^2 + 6)*(x - 8x + 3x^3), the product rule is applied multiple times to find the derivative of the entire expression.
  • 📊 To evaluate f*g' at a specific point, simply substitute the values of f, f', g, and g' at that point into the formula f'*g + f*g'.
  • 🔍 When given values for f and g at a certain point, along with their derivatives, you can directly calculate f*g' using the provided information.
  • 🧠 Understanding the product rule is crucial for differentiating more complex functions involving multiplication of several functions.
  • 📝 The product rule is a fundamental tool in calculus that extends the basic rules of differentiation to handle more intricate scenarios.
  • 🌐 The examples provided in the script demonstrate the application of the product rule in various contexts, highlighting its versatility and importance in solving derivative problems.
Q & A

  • What is the product rule for derivatives mentioned in the transcript?

    -The product rule for derivatives states that the derivative of a product of two functions, f and g, is the derivative of f times g plus f times the derivative of g.

  • How is the derivative of the function f(x) = x^2 * sin(x) calculated using the product rule?

    -To calculate the derivative of f(x) = x^2 * sin(x) using the product rule, first identify f as x^2 and g as sin(x). Then find their derivatives, f' = 2x and g' = cos(x). Apply the product rule: f'g + fg', which gives (2x)(sin(x)) + (x^2)(cos(x)). This can be factored out to x(2sin(x) + x*cos(x)).

  • What is the derivative of the expression (5x - 9x^3) * (8 + x^2)?

    -To find the derivative of the expression (5x - 9x^3) * (8 + x^2), apply the product rule. Let f(x) = 5x - 9x^3 and g(x) = 8 + x^2. Calculate f'(x) = 5 - 27x^2 and g'(x) = 2x. Then, use the formula (f'g + fg'). The derivative is (5 - 27x^2)(8 + x^2) + (5x - 9x^3)(2x), which simplifies to 5x + 4x^3 - 8x^3 - 9x^5.

  • How does the product rule apply to trigonometric functions in the given examples?

    -The product rule applies to trigonometric functions by first identifying the functions f and g, finding their derivatives, and then applying the rule (f'g + fg'). For instance, with 4sin(x)tan(x), f' is 4cos(x) and g' is sec^2(x). The derivative is 4cos(x) * tan(x) + 4sin(x) * sec^2(x), simplifying to 4sin(x)sec^2(x) + 4cos(x)tan(x).

  • What is the process for differentiating a function with three factors using the product rule?

    -For a function with three factors, say f(x) * g(x) * h(x), apply the product rule in a stepwise manner. First, differentiate f(x) and keep g(x) and h(x) unchanged. Then, differentiate g(x) with f(x) and h(x) unchanged, and finally, differentiate h(x) with both f(x) and g(x) unchanged. Then apply the product rule formula (f'g + fg')(h) + (f'g + fg')(h) + (fh' + fgh').

  • How can the product rule be used to evaluate the expression (f * g)'(x) at a specific value?

    -To evaluate (f * g)'(x) at a specific value, use the product rule formula (f'g + fg'). Plug in the values of f'(x), f(x), g'(x), and g(x) at the given x-value. For example, if f'(3) = -7, f(3) = 4, g'(3) = 5, and g(3) = -8, then (f * g)'(3) = f'(3) * g(3) + f(3) * g'(3) = -7 * -8 + 4 * 5 = 56 + 20 = 76.

  • What is the significance of the product rule in calculus?

    -The product rule is a fundamental tool in calculus for finding the derivatives of composite functions. It extends the basic rules of differentiation to more complex scenarios where functions are multiplied together, allowing for the analysis of rates of change in various contexts, such as physics and engineering.

  • How does factoring out common terms help in simplifying the derivative of a function?

    -Factoring out common terms from the derivative of a function simplifies the expression, making it easier to interpret and work with. For example, in the derivative of x^2 * sin(x), factoring out x results in a simplified expression of 2sin(x) + x*cos(x), which is more manageable for further calculations or analysis.

  • What is the role of the constant in the product rule?

    -In the product rule, the derivative of a constant multiplied by a function is simply the constant multiplied by the derivative of the function. This is because the constant does not change with respect to the variable, so its rate of change is zero.

  • How does the chain rule relate to the product rule?

    -The chain rule and the product rule are both used to differentiate composite functions. The chain rule is used when a function is a composition of others, while the product rule applies when two or more functions are multiplied together. Both rules are essential for advanced differentiation techniques in calculus.

  • What is the general process for differentiating a complex function?

    -The general process for differentiating a complex function involves identifying the type of function (e.g., polynomial, trigonometric, exponential), applying the appropriate rules (e.g., power rule, product rule, chain rule), and simplifying the result if possible. This process often requires breaking down the function into simpler parts and working with each part separately.

  • What are some common mistakes to avoid when using the product rule?

    -Common mistakes when using the product rule include forgetting to multiply by the original function (fg') or the original part (f'g), omitting the negative sign when differentiating a term with a negative coefficient, and not factoring out common terms to simplify the expression.

Outlines
00:00
📚 Introduction to the Product Rule for Derivatives

This paragraph introduces the product rule for calculating derivatives of functions. It explains that the derivative of a product of two functions, f(x) and g(x), is equal to f'(x)g(x) + f(x)g'(x). The explanation is supported with examples, such as finding the derivative of x^2 * sin(x), and demonstrates the process of applying the product rule step by step. The paragraph also includes a simplification technique, where a common factor (in this case, x) is factored out from the result. Another example is given, involving a more complex expression, 5x - 9x^3 * (8 + x^2), and the process of finding its derivative using the product rule is detailed. The explanation is clear, showing the step-by-step differentiation of each term and combining them to get the final derivative.

05:04
🔢 Applying the Product Rule to Trigonometric Functions

This paragraph delves into applying the product rule to functions involving trigonometric functions. It starts with an example of a function, f(x) = 4 * sin(x) * tan(x), and breaks it down into two parts for easier differentiation. The derivative of the first part, 4 * sin(x), is calculated as 4 * cos(x), and the derivative of the second part, tan(x), is found to be sec^2(x). The paragraph then explains the process of simplifying the expression by canceling out common terms. Another example follows, this time with a function, f(x) = 5x * sin(x) - x^3 * tan(x), where the product rule is applied to each term separately. The derivatives are calculated and combined, with attention to detail such as distributing the negative sign correctly. The paragraph concludes with a clear and comprehensive summary of the steps taken to find the derivative of the given function.

10:06
📈 Evaluating Derivatives with Given Values

The final paragraph discusses how to evaluate the derivative of a product of functions when given specific values for the functions and their derivatives. It introduces a scenario where f(x) = x^2 + 6, g(x) = 7 - 8x, and h(x) = 3x^3, and the task is to find the derivative, r'(x), when x = 3. The paragraph explains that the product rule can be extended to more than two functions by differentiating each function one at a time and combining the results. The process is demonstrated with a clear breakdown of the steps, leading to the calculation of r'(x). The paragraph then presents another scenario where the values of f(x), f'(x), g(x), and g'(x) are given, and it shows how to evaluate the expression f'(x)g(x) + f(x)g'(x) at x = 3. The explanation is straightforward and easy to follow, illustrating the practical application of the product rule in evaluating derivatives at specific points.

Mindmap
Keywords
💡Product Rule
The Product Rule is a fundamental rule in calculus for finding the derivative of a product of two functions. It states that the derivative of a function f multiplied by another function g is equal to the derivative of f times g plus f times the derivative of g. This rule is central to the video's theme as it is used to solve various examples of differentiating composite functions.
💡Derivatives
Derivatives are a core concept in calculus that represent the rate of change or slope of a function at a particular point. They are used to analyze the behavior of functions, such as determining local maxima or minima, and the rate of change of quantities. In the video, the calculation of derivatives is the primary focus, with several examples illustrating how to find the derivative of different functions.
💡Function
In mathematics, a function is a relation that maps each element from one set (the domain) to exactly one element in another set (the codomain). Functions are central to the video's content as they are the objects whose derivatives are being calculated and analyzed using the Product Rule.
💡Sine and Cosine
Sine and cosine are trigonometric functions that relate the angles and sides of a right triangle. They are periodic functions commonly used in solving problems involving oscillations, waves, and circular motion. In the video, sine and cosine are used as part of the functions being differentiated, showcasing their derivatives as cos x and -sin x respectively.
💡Tangent
The tangent function, often abbreviated as tan, is a trigonometric function that finds the ratio of the opposite side to the adjacent side in a right triangle. It is also used to describe the slope of a line. In the context of the video, the derivative of the tangent function is shown to be secant squared, which is a less common but important result in calculus.
💡Power Rule
The Power Rule is a basic rule in calculus that allows for the differentiation of functions raised to a power. It states that the derivative of x^n, where n is any real number, is n*x^(n-1). This rule is essential for differentiating monomials and is used in the video when finding the derivative of terms like x^3 or 9x^3.
💡Constant
In mathematics, a constant is a value that does not change. In the context of calculus, the derivative of a constant is always zero because a constant does not vary with respect to the independent variable. The video mentions that the derivative of a constant is zero when applying the Product Rule to differentiate expressions involving constants.
💡Factoring
Factoring is the process of breaking down a polynomial into its constituent factors, which are simpler expressions. In the context of the video, factoring is used as a simplification technique after applying the Product Rule to certain expressions, making them easier to work with or interpret.
💡Differentiation
Differentiation is the process of finding the derivative of a function, which describes how the function changes as its input changes. It is a fundamental operation in calculus and is the primary operation demonstrated in the video.
💡Secant Function
The secant function, written as sec, is a trigonometric function that is the reciprocal of the cosine function, or 1/cos(x). It is used in advanced trigonometry and calculus, particularly when dealing with the slopes of lines and hyperbolic functions. In the video, the derivative of the tangent function is given as secant squared, which is derived from the relationship between tangent and cosine.
💡Chain Rule
The Chain Rule is a fundamental concept in calculus that is used to find the derivative of a composite function, which is a function made up of one function nested inside another. While not explicitly named in the video, the Chain Rule is implied when differentiating complex expressions that involve the product of multiple functions.
Highlights

Introduction to the product rule for derivatives, a fundamental concept in calculus.

Derivative of a product of two functions, f(x)g(x), is f'(x)g(x) + f(x)g'(x), explained with clarity.

Example provided: derivative of x^2 * sin(x) using the product rule, showcasing the practical application of the concept.

Detailed explanation of finding the derivative of each component function before applying the product rule.

Demonstration of factoring out the greatest common factor (GCF) to simplify the derivative expression.

Second example: differentiating the expression (5x - 9x^3) * (8 + x^2), illustrating the product rule with more complex functions.

Explanation of how to handle constants and their derivatives within the product rule.

Use of the power rule to find the derivative of x^2 in the example, reinforcing fundamental calculus techniques.

Example with trigonometric functions: differentiating 4sin(x) * tan(x), demonstrating the application of the product rule in trigonometry.

Clarification on the derivative of tangent as secant squared, and the process of simplifying trigonometric derivatives.

Another example: differentiating 5x * sin(x) - x^3 * tan(x), showing the product rule applied to multiple terms.

Explanation of distributing the negative sign when applying the product rule to expressions with multiple terms.

Handling a product of three functions using the product rule, extending the concept to more than two functions.

Given values for f(3), f'(3), g(3), and g'(3), and how to evaluate f'g + fg' at a specific point using these values.

Emphasis on the importance of accurate sign distribution when applying the product rule to expressions with negative terms.

Concluding remarks, summarizing the video's content and expressing gratitude to the viewers for their attention.

Transcripts

Browse More Related Video

Product Rule for Derivatives

Math 1325 Lecture 9 5 - Product & Quotient Rule

Taking the derivative of two binomials using product and chain rule

Higher Order Derivatives

Product rule proof | Taking derivatives | Differential Calculus | Khan Academy

Simplifying Derivatives

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Derivative RulesProduct RuleCalculus TutorialMath EducationTrigonometric FunctionsAlgebraic DifferentiationComplex FunctionsMathematical SimplificationEducational ContentOnline Learning