Quotient Rule for Derivatives

Professor Monte
9 Jun 202006:40
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging calculus tutorial, Professor Monte dives into the intricacies of the quotient rule for derivatives. He begins by introducing the rule with a memorable jingle, 'low D high minus high D low, square the bottom and away we go,' emphasizing the importance of the order for accuracy. The professor then illustrates the rule's application with two examples. The first example involves differentiating f(x) = x^8 / x^2, which simplifies to 6x^5, confirming the rule's validity. The second example tackles H(x) = x^3 / (4x - 6), a more complex function that cannot be simplified beforehand. Throughout the lesson, Professor Monte stresses the significance of maintaining the correct sign and order to avoid errors. He encourages practice and provides a light-hearted approach to mastering the quotient rule, leaving students with the confidence that they too can excel in calculus.

Takeaways
  • 📚 The quotient rule for derivatives is a method for finding the derivative of a function that is the quotient of two other functions.
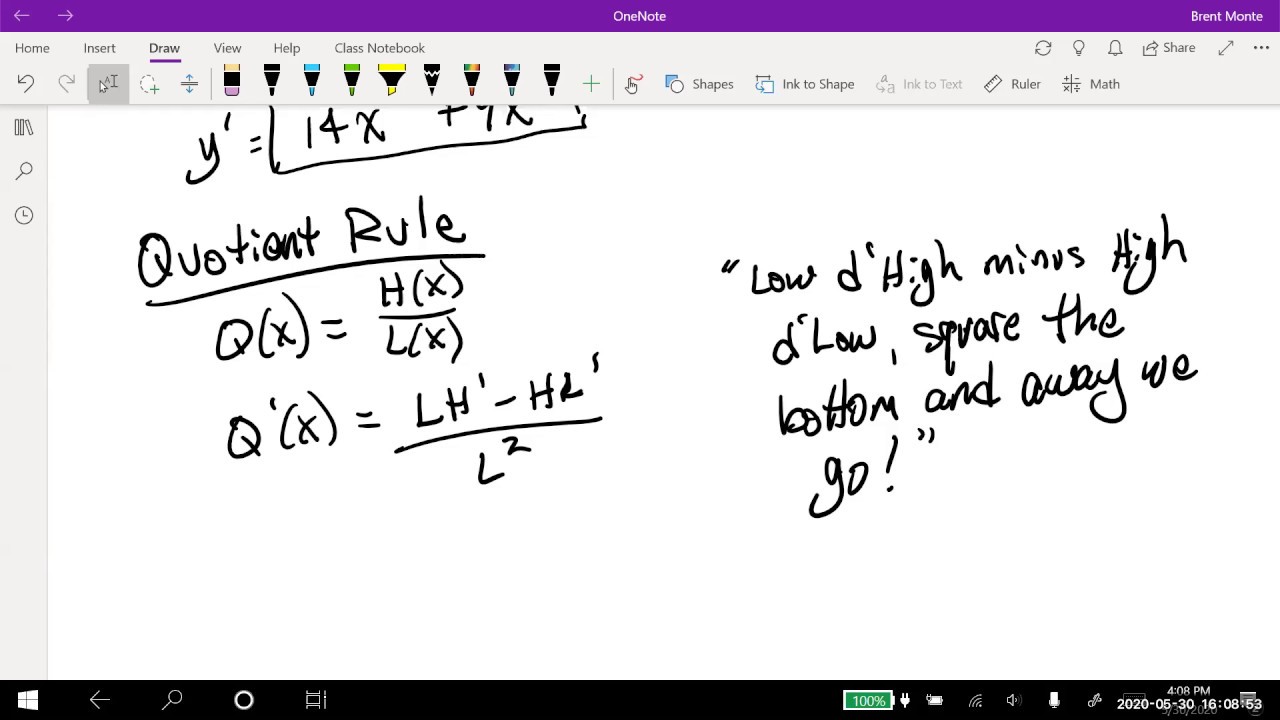
  • 🔢 The rule is expressed as (Q(x))' = (L(x) * (H(x))' - H(x) * (L(x))') / (L(x)^2), where H(x) is the high function and L(x) is the low function.
  • 🎓 Professor Monte uses the mnemonic 'low D high minus high D low, square the bottom and away we go' to help remember the quotient rule.
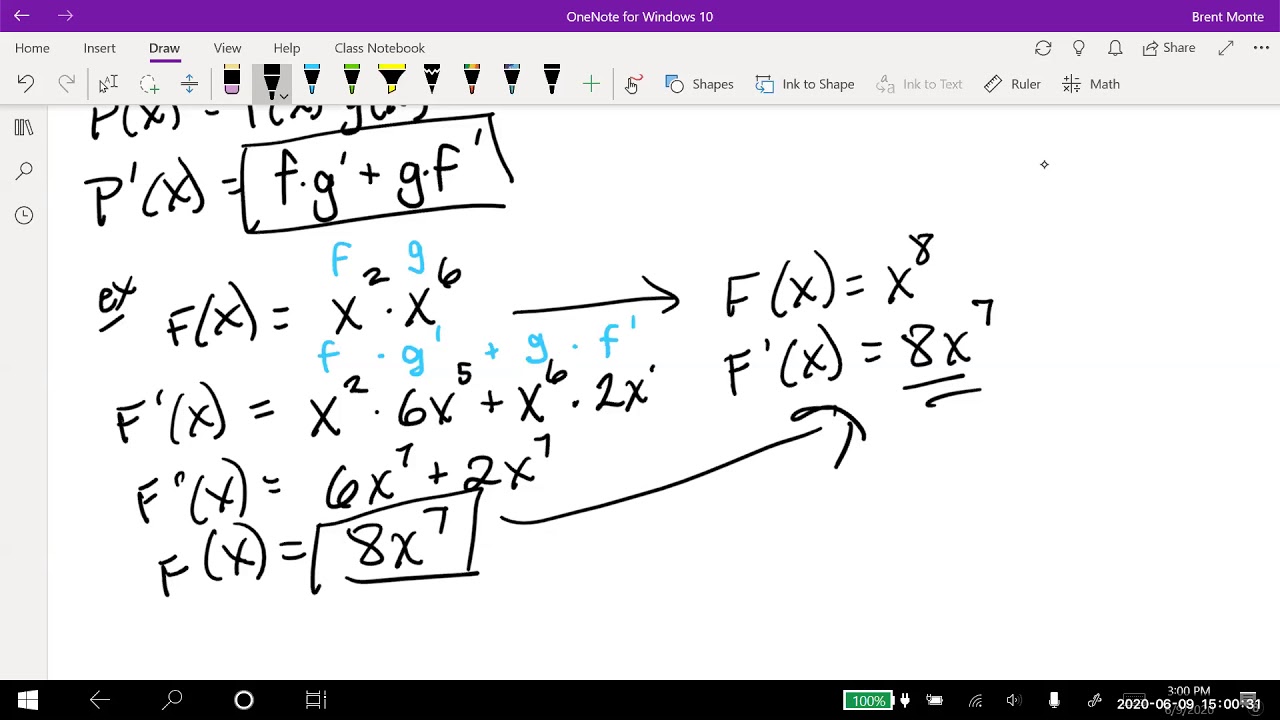
  • ✅ An example given is f(x) = (x^8 / x^2), which simplifies to x^6 and its derivative, using the quotient rule, is 6x^5.
  • 📉 When you can't simplify the functions first, the quotient rule is essential to find the derivative directly.
  • 🤔 The importance of keeping the correct order of subtraction in the numerator is emphasized to avoid incorrect signs in the derivative.
  • 📝 For the function H(x) = x^3 and L(x) = 4x - 6, the quotient rule is applied to find the derivative without simplifying first.
  • 🧮 Distributing the terms in the numerator and combining like terms is a part of the process to find the derivative using the quotient rule.
  • 📊 The quotient rule allows you to find the derivative of complex functions that are not easily simplified, which is crucial for finding maximum and minimum values.
  • 📈 The process involves careful attention to detail, ensuring that the signs and order of operations are correct to get the accurate derivative.
  • 🌟 Practice is encouraged to become proficient with the quotient rule, and a jingle can be a helpful tool for remembering the rule's structure.
  • 📺 Subscribing and commenting on Professor Monte's videos can provide additional insights and access to a wider range of calculus topics.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the quotient rule for derivatives in calculus.

  • What is the quotient rule for derivatives?

    -The quotient rule for derivatives states that the derivative of a quotient of two functions is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.

  • What is the mnemonic provided by Professor Monte to remember the quotient rule?

    -The mnemonic provided by Professor Monte is 'low D high minus high D low, square the bottom and away we go'.

  • What is the significance of the order of terms in the quotient rule?

    -The order of terms in the quotient rule is crucial as reversing the order can lead to the wrong sign in the derivative, which would result in an incorrect answer.

  • How does the video demonstrate the quotient rule with an example?

    -The video demonstrates the quotient rule by applying it to the function f(x) = x^8 / x^2, showing each step of the calculation and simplifying to obtain the correct derivative, 6x^5.

  • What is the importance of not simplifying the denominator before applying the quotient rule?

    -Simplifying the denominator before applying the quotient rule can lead to incorrect results. It is important to apply the rule directly to the original expression to ensure the correct derivative is obtained.

  • Why does Professor Monte recommend practicing the quotient rule?

    -Professor Monte recommends practicing the quotient rule to improve understanding and proficiency. With practice, students can apply the rule more accurately and efficiently.

  • What is the second example function used in the video to demonstrate the quotient rule?

    -The second example function used in the video is h(x) = x^3 / (4x - 6), which cannot be simplified before applying the quotient rule.

  • How does the video handle the calculation of the derivative for the second example?

    -The video applies the quotient rule directly to the second example, distributing the terms and combining like terms to find the derivative, without simplifying the denominator.

  • What is the final answer for the derivative of the second example function?

    -The final answer for the derivative of the second example function is 8x^3 - 18x^2 - 4x^3, which simplifies to 4x^2 - 12x.

  • Why does the video emphasize the importance of factoring out the top terms in the derivative?

    -Factoring out the top terms in the derivative can help simplify the expression and make it easier to solve for maximum and minimum values. However, it is not always necessary for simply finding the derivative.

  • What does Professor Monte encourage viewers to do if they like the video?

    -Professor Monte encourages viewers to subscribe to his channel and leave comments if they want to see more videos on specific topics.

Outlines
00:00
📚 Introduction to the Quotient Rule for Derivatives

Professor Monte introduces the concept of the quotient rule for derivatives, which is essential for differentiating complex functions. He uses the notation 'H' for the high function (numerator) and 'L' for the low function (denominator) to illustrate the rule: low D high minus high D low, all squared at the bottom. The professor emphasizes the importance of the order of operations and provides a mnemonic to help remember it: 'low D high minus high D low, square the bottom and away we go.' He then applies the rule to a simplified example, f(x) = x^8 / x^2, to demonstrate how the rule works in practice, resulting in the derivative 6x^5.

05:03
🔢 Applying the Quotient Rule to Non-Simplified Functions

The professor continues by applying the quotient rule to a function that cannot be simplified first, specifically f(x) = x^3 / (4x - 6). He demonstrates the step-by-step process of differentiating using the quotient rule, emphasizing the need to maintain the correct order of operations to avoid errors in sign. The calculation involves distributing the derivative of the high function (3x^2) across the terms of the low function (4x - 6), resulting in a derivative expression that includes terms like 12x^3 and -18x^2. The professor advises against unnecessarily simplifying the expression if the goal is only to find the derivative, but notes that factoring out terms can be beneficial for further analysis, such as finding maximum and minimum values.

Mindmap
Keywords
💡Quotient Rule
The Quotient Rule is a fundamental theorem in calculus for finding the derivative of a function that is the quotient of two other functions. It states that the derivative of a function Q(x) = H(x) / L(x) is given by Q'(x) = (L(x) * H'(x) - H(x) * L'(x)) / (L(x))^2. In the video, Professor Monte uses the Quotient Rule to derive the derivatives of given functions, demonstrating its application in simplifying complex differentiation problems.
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. It is a measure of the sensitivity to change of the function value. In the context of the video, derivatives are calculated using various rules, including the Quotient Rule, to understand how functions behave as their inputs change.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. An example from the video is f(x) = x^8 / x^2, which is a specific case used to illustrate the application of the Quotient Rule.
💡Exponents
Exponents are a mathematical notation indicating the number of times a base appears in a multiplication. In the video, exponents are used in functions such as x^8 and x^2, and their manipulation is key to simplifying expressions and applying the Quotient Rule correctly.
💡Simplify
To simplify in mathematics means to reduce a complex expression to a more straightforward or standard form. In the context of the video, simplifying is an important step after applying the Quotient Rule to make the derivative easier to understand and work with, as demonstrated with the function f(x) = x^8 / x^2.
💡High and Low
In the context of the Quotient Rule, 'High' refers to the numerator function H(x), and 'Low' refers to the denominator function L(x). Professor Monte uses these terms as a mnemonic to remember the order and structure of the Quotient Rule formula.
💡Mnemonic
A mnemonic is a memory aid or formula used to help remember complex information. Professor Monte uses the phrase 'low D high minus high D low, square the bottom and away we go' as a mnemonic to help students remember the structure of the Quotient Rule.
💡Differentiation
Differentiation is the process of finding the derivative of a function. It is a core operation in calculus and is used to analyze the behavior of functions, including their rates of change and critical points. The video focuses on differentiation using the Quotient Rule.
💡Like Terms
Like terms in algebra are terms that have the same variables raised to the same powers. When applying the Quotient Rule, like terms are combined or simplified to reduce the complexity of the resulting derivative, as shown when Professor Monte simplifies 8x^9 - 2x^9 over x^4.
💡Factoring
Factoring is the process of breaking down an expression into a product of its factors. In the video, factoring is mentioned as a potential step after differentiating, particularly if the derivative is to be further simplified or if solving for maximum and minimum values is required.
💡Max and Min Values
Max and Min values refer to the maximum and minimum points of a function, respectively. These are critical points where the derivative is zero or undefined. Factoring the derivative, as mentioned in the video, can help in finding these points, although it is not always necessary for simply calculating the derivative.
Highlights

Professor Monte introduces the quotient rule for derivatives, a fundamental concept in calculus.

The quotient rule is expressed as 'low D high minus high D low, square the bottom and away we go', a mnemonic to help remember the formula.

The use of 'H' for the high function and 'L' for the low function in the quotient rule is explained for clarity.

An example is given where f(x) = x^8 / x^2, demonstrating the application of the quotient rule.

The derivative of the example is simplified to 6x^5, verifying the quotient rule's accuracy.

The importance of not simplifying the functions before applying the quotient rule is emphasized.

A second example is provided with f(x) = x^3 / (4x - 6), a case where simplification is not possible before applying the rule.

The quotient rule is applied to the second example, maintaining the correct order of terms to get the correct sign in the derivative.

The process of distributing and combining like terms in the derivative is demonstrated step by step.

The video stresses the significance of not foiling out the bottom terms to maintain the factored form useful for finding max/min values.

The quotient rule is shown to be applicable even when the functions cannot be simplified, making it a versatile tool in calculus.

Professor Monte encourages students to practice the quotient rule to improve their proficiency with it.

A jingle is suggested as a memory aid for the order of terms in the quotient rule.

The video concludes with an encouragement to subscribe for more calculus content and to leave comments for additional topic requests.

The transcript provides a comprehensive guide to understanding and applying the quotient rule in calculus.

The practical application of the quotient rule is demonstrated through step-by-step examples.

The video aims to demystify calculus concepts and make them more accessible to learners.

The importance of correct sign in the derivative is highlighted, emphasizing the precision required in calculus.

Transcripts

Browse More Related Video

Product Rule for Derivatives

Math 11 - Section 1.6

Math 11 - Sections 1.7-1.8

The Quotient Rule for Derivatives — Topic 58 of Machine Learning Foundations

Integration by Substitution

Higher Order Derivatives!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusDerivativesQuotient RuleEducationalMathematicsProfessor MonteLearningSimplificationFunction AnalysisExponent RulesWebinar