Solving Logarithms with Common Bases (Precalculus - College Algebra 62)
TLDRIn this educational video, the presenter dives into the process of solving logarithmic equations with a focus on a special case where all terms in the equation are logarithms with the same base. The video outlines a straightforward method for solving such equations by setting the arguments (or 'insides') of the logarithms equal to each other, drawing parallels to the process used in solving exponential equations with common bases. The presenter emphasizes the importance of considering the domain of logarithms, which requires the argument to be strictly greater than zero. The script also touches on the general approach to solving logarithmic equations, which often involves converting logarithms to exponentials. The video is structured to first introduce the special case, then build up to more complex scenarios where exponentials are necessary, setting the stage for the next video in the series.
Takeaways
- 📚 **Special Case of Logarithms**: When solving logarithms with the same base, if all terms are logarithms, you can combine them and set the arguments equal to each other.
- 🔑 **Base Equality**: The method of setting logarithms equal only works if every term in the equation is a logarithm with the same base.
- 🚫 **No General Case**: This approach does not apply to the general case of logarithmic equations, which often require the use of exponentials for solving.
- 🧐 **Domain Consideration**: When dealing with logarithms, remember that the argument (inside the logarithm) must always be greater than zero.
- 🔢 **Combining Logarithms**: Combine logarithms by adding or subtracting them to form a single logarithm, moving coefficients as exponents.
- 🆗 **Solution Validation**: After finding a solution, verify that it does not result in a negative or zero argument for any logarithm in the original equation.
- ✅ **Example Solved**: The script provides a step-by-step solution to the equation log base 4 of x + 2 = log base 4 of 8, resulting in x = 6.
- 🤔 **Categorization of Equations**: Before solving, categorize logarithmic equations based on whether all logs have the same base or if there are different bases or constants involved.
- 📉 **Handling Different Bases**: If logarithms have different bases or there's a constant, the special case approach does not apply, and you may need to use exponentials.
- 🤓 **Exponentials as Inverse**: In general, to solve logarithmic equations, you'll need to use the concept of exponentiation as the inverse operation to logarithms.
- ⏯ **Transition to General Case**: The script previews the approach for solving general logarithmic equations in the next video, which involves using exponentials when direct comparison of logarithms isn't possible.
Q & A
What is the special case for solving logarithms discussed in the video?
-The special case discussed is when every term in an equation is a logarithm with the same base. In such a case, the logarithms can be combined into one logarithm on each side of the equation, and then the arguments (insides) of the logarithms can be set equal to each other.
Why is it necessary to check the solutions when solving logarithmic equations?
-It is necessary to check the solutions to ensure that the insides of the logarithms do not become negative. Since the domain of a logarithm requires its argument to be strictly greater than zero, any solution that results in a negative or zero value inside the logarithm is invalid.
How does the process of solving logarithms with common bases relate to solving exponentials with common bases?
-The process is similar in that if the bases are the same, then the exponents (or in the case of logarithms, the arguments) must also be equal to maintain the equality. This is because logarithms and exponentials are inverse functions, and applying the same operation to both sides of an equation involving inverse functions preserves equality.
What is the first step when combining logarithms with the same base?
-The first step is to move any coefficients in front of the logarithms as exponents. Then, combine the logarithms by adding or subtracting them to form a single logarithm on each side of the equation, following the rules for combining logarithms (addition results in multiplication, and subtraction results in division).
Why is it not always necessary to use exponentials to solve logarithmic equations?
-Exponentials are not always necessary when solving logarithmic equations because there is a special case where if all terms are logarithms with the same base, they can be combined and set equal to each other directly without the need for converting to exponential form.
What is the domain restriction for logarithmic expressions?
-The domain restriction for logarithmic expressions is that the argument (the value inside the logarithm) must be strictly greater than zero. Logarithms are not defined for non-positive numbers.
How can you simplify the equation log base 4 of x plus 2 equals log base 4 of 8?
-By recognizing that both sides of the equation have logarithms with the same base, you can set the arguments equal to each other. This simplifies to x plus 2 equals 8. Solving for x gives x equals 6, which can be verified by substituting back into the original logarithmic equation.
What is the process for combining logarithms with different coefficients?
-When combining logarithms with different coefficients, you first move the coefficients as exponents on their respective arguments. Then, if the logarithms are being added, the arguments are multiplied. If they are being subtracted, the arguments are divided. This process creates a single logarithm on each side of the equation.
How does the video script differentiate between logarithmic equations that require exponentials and those that do not?
-The script differentiates by checking if all terms in the logarithmic equation are logarithms with the same base. If so, they can be combined and set equal to each other without using exponentials. If there are different bases or constants involved, then exponentials are typically required to solve the equation.
What is the zero product property mentioned in the context of solving equations?
-The zero product property states that if a product of two factors equals zero, then at least one of the factors must be zero. This property is used in the context of solving equations by setting the product of factors equal to zero and solving for the variables.
Why is it important to consider the domain when combining logarithms with division?
-Considering the domain is important because logarithms are only defined for arguments that are strictly greater than zero. When combining logarithms with division, you must ensure that the resulting argument does not violate this domain restriction, meaning it should not be zero or negative.
Outlines
📚 Introduction to Solving Logarithms with Same Base
This paragraph introduces the topic of solving logarithms and exponential equations. It emphasizes a special case where all terms in an equation are logarithms with the same base, which can be solved by setting the arguments of the logarithms equal to each other. The video also notes that this method is not general and that exponentials will be needed for other cases. The importance of considering the domain of logarithms, which requires the argument to be strictly greater than zero, is highlighted. An example problem is presented to illustrate the process.
🔍 Combining Logarithms with Same Base
The paragraph explains how to combine logarithms with the same base by turning coefficients into exponents and setting the arguments equal when both sides of an equation have a single logarithm each. It also discusses the process of using exponentials to solve logarithmic equations when the bases are not the same or when there are constants involved. The paragraph further illustrates how to handle logarithms with different coefficients and how to check solutions to ensure they do not result in negative or zero arguments within the logarithms.
🧮 Dealing with Logarithms and Exponentials
This section delves into the process of solving logarithmic equations by transforming them into exponential form. It discusses the conditions under which logarithms with the same base can be equated and solved using basic algebraic techniques. The paragraph also addresses the concept of logarithms having a vertical asymptote at zero, implying that the argument of a logarithm cannot be zero or negative. The process of combining logarithms and then solving the resulting equation is demonstrated through an example.
📝 Categorizing Logarithmic Equations
The paragraph focuses on categorizing logarithmic equations based on whether all terms are logarithms with the same base. It explains that if this condition is met, the logarithms can be combined and their arguments set equal to each other. The process of moving coefficients to exponents and combining logarithms into a single logarithm is detailed. The importance of checking solutions to ensure they do not violate the domain of logarithms is reiterated.
🔢 Solving Logarithms Using Exponentials
This part of the script explores the alternative method of solving logarithmic equations using exponentials. It demonstrates how to gather all logarithmic terms on one side of the equation and a constant on the other, then transform the equation into an exponential form. The process involves combining logarithms, moving coefficients to exponents, and ensuring that the logarithms have the same base. The solution is checked to confirm it does not result in a negative or zero argument for the logarithm.
🎯 Identifying Valid Solutions for Logarithms
The paragraph discusses the process of identifying valid solutions for logarithmic equations. It emphasizes that when all terms are logarithms with the same base, they can be combined and set equal to each other. The video provides an example of solving such an equation and checking the solution to ensure it does not lead to a negative or zero inside the logarithm. It also previews the approach for solving logarithms that require exponentials, which will be covered in the next video.
📉 Generalizing the Solution Process for Logarithms
The final paragraph summarizes the process for solving logarithmic equations, highlighting the special case where all terms are logarithms with the same base and can be directly equated. It contrasts this with the general case where exponentials are necessary to solve the equation. The paragraph also demonstrates how to write a logarithmic equation in exponential form to find the solution. The video concludes by reiterating the importance of checking solutions to maintain the domain restrictions of logarithms.
Mindmap
Keywords
💡Logarithms
💡Exponential Equations
💡Common Base
💡Combining Logarithms
💡Domain
💡Arguments of Logarithms
💡Coefficients as Exponents
💡Zero Product Property
💡Cube Root
💡Exponential as Inverse
💡Solving Logarithmic Equations
Highlights
The video focuses on solving logarithms and exponential equations with a special case where all terms are logarithms of the same base.
If all terms in an equation are logarithms with the same base, they can be combined into a single logarithm on each side of the equation.
To solve logarithms with the same base, set the arguments (insides) of the logarithms equal to each other, similar to solving exponentials with common bases.
The general case for solving logarithmic equations requires the use of exponentials, except for the special case with common bases.
When combining logarithms, coefficients in front of the logarithms can be moved as exponents.
Logarithms must have strictly positive arguments, and solutions should be checked to ensure they do not result in negative or zero inside the logarithms.
An example is provided where log base 4 of x plus 2 equals log base 4 of 8, leading to the solution x equals 6 after simplification.
Different methods for solving logarithms are discussed, including the use of exponentials and combining logarithms with the same base.
The process of combining logarithms involves moving coefficients as exponents and creating a single logarithm with a fraction if necessary.
The video emphasizes the importance of checking solutions to ensure they do not violate the domain of logarithms, which requires positive arguments.
An alternative method using exponentials is introduced as a transition to solving more general logarithmic equations in the next video.
The video concludes with the approach of gathering all logarithms on one side and a constant on the other to prepare for using an exponential to solve the equation.
The zero product property is mentioned as a technique for solving equations when a power of two or higher is involved.
The video demonstrates that whether distributing first or creating a fraction, the process of combining logarithms with the same base will yield the same result.
The distinction between logarithms with the same base and those requiring exponentials for solving is clarified through examples and explanations.
The video provides a comprehensive understanding of solving logarithms with the same base as a special case before moving on to more complex logarithmic equations.
The concept of logarithms and exponentials being inverse functions is used to transition from logarithmic to exponential form for solving equations.
The video concludes by emphasizing that while special cases can simplify the process, general logarithmic equations are solved using exponentials.
Transcripts
Browse More Related Video
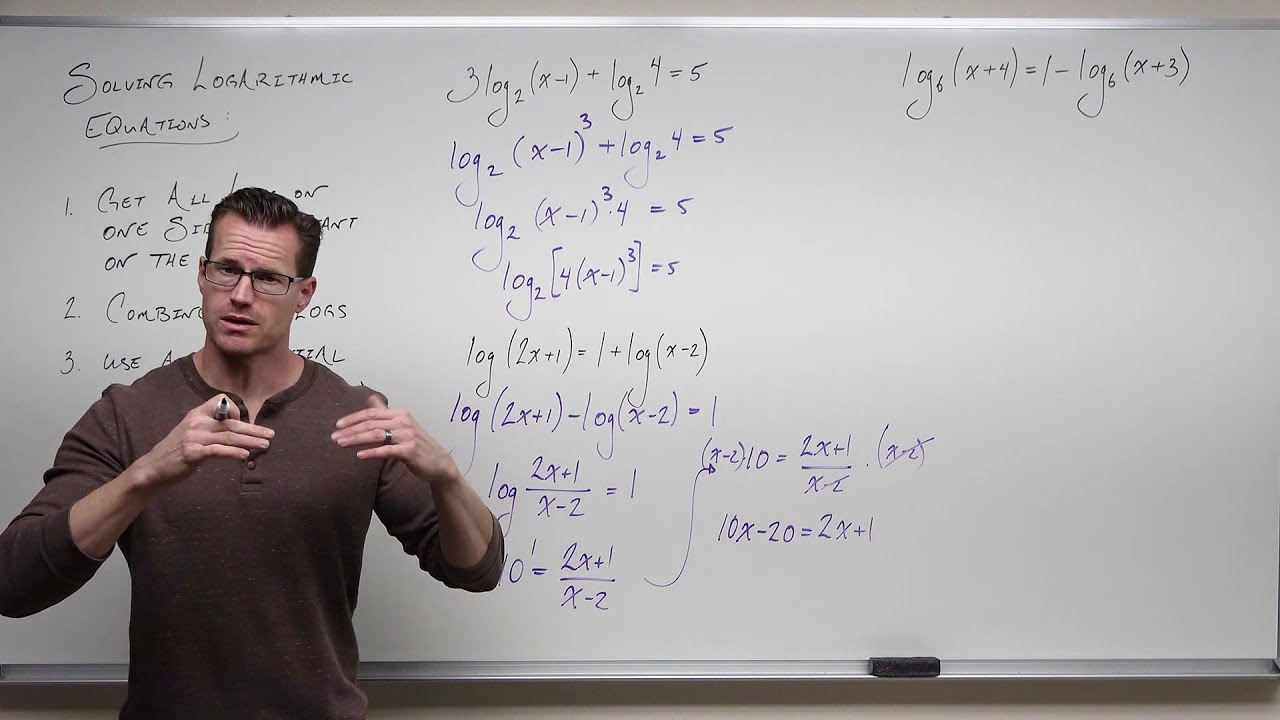
Solving Logarithmic Equations with Exponentials (Precalculus - College Algebra 63)

Solving Exponential Equations with Common Bases (Precalculus - College Algebra 54)

Introduction to Solving Logarithms and Exponentials (Precalculus - College Algebra 57)

Solving Exponential Equations with Logarithms (Precalculus - College Algebra 64)
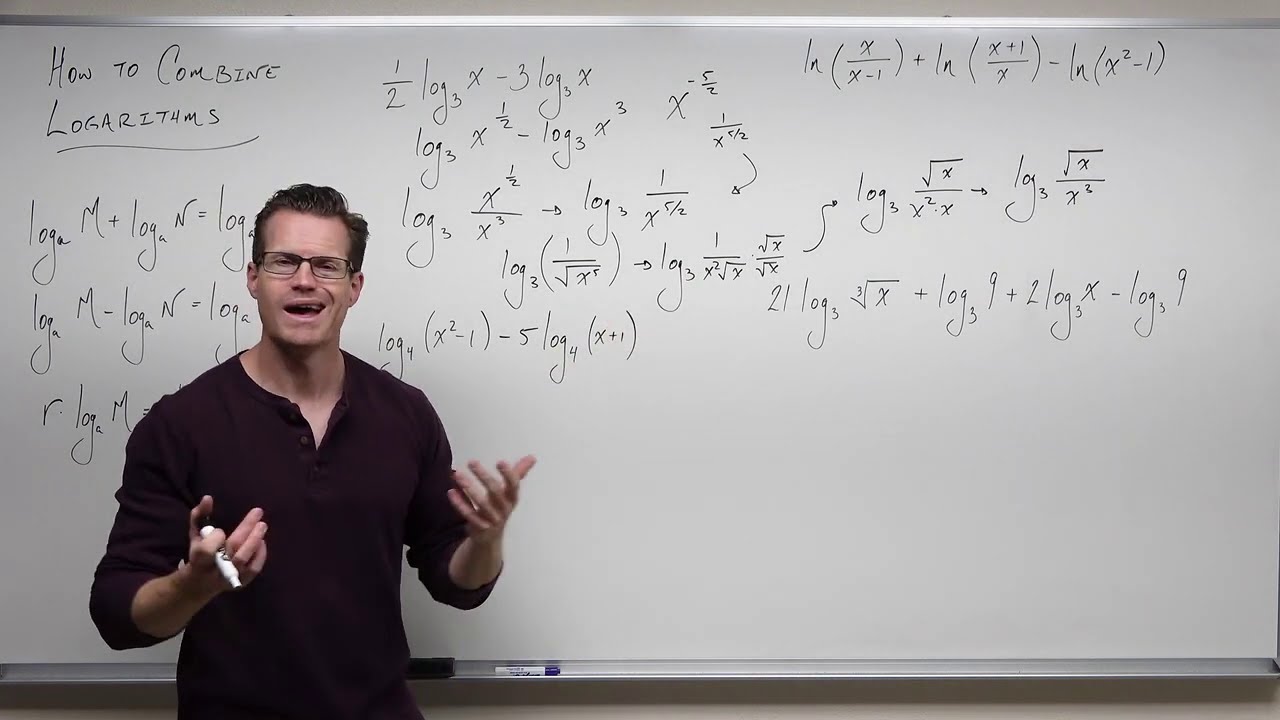
How to Combine Logarithms (Precalculus - College Algebra 60)

Bases other than e
5.0 / 5 (0 votes)
Thanks for rating: